GIÁO ÁN ĐIỆN TỬ - DIỄN ĐÀN GIÁO VIÊN TOÁN
TOÁN
LỚP
12 THPT
GIẢI TÍCH
Chương 3: Phương pháp tọa độ trong mặt
phẳng
LỚP
12
CÁC VÍ DỤ MINH HỌA
II
HỆ THỐNG KIẾN THỨC
I
ÔN TẬP CHƯƠNG (tiết 1)
BÀI TẬP TRẮC NGHIỆM
GIÁO ÁN ĐIỆN TỬ - DIỄN ĐÀN GIÁO VIÊN TOÁN
TOÁN
LỚP
12 THPT
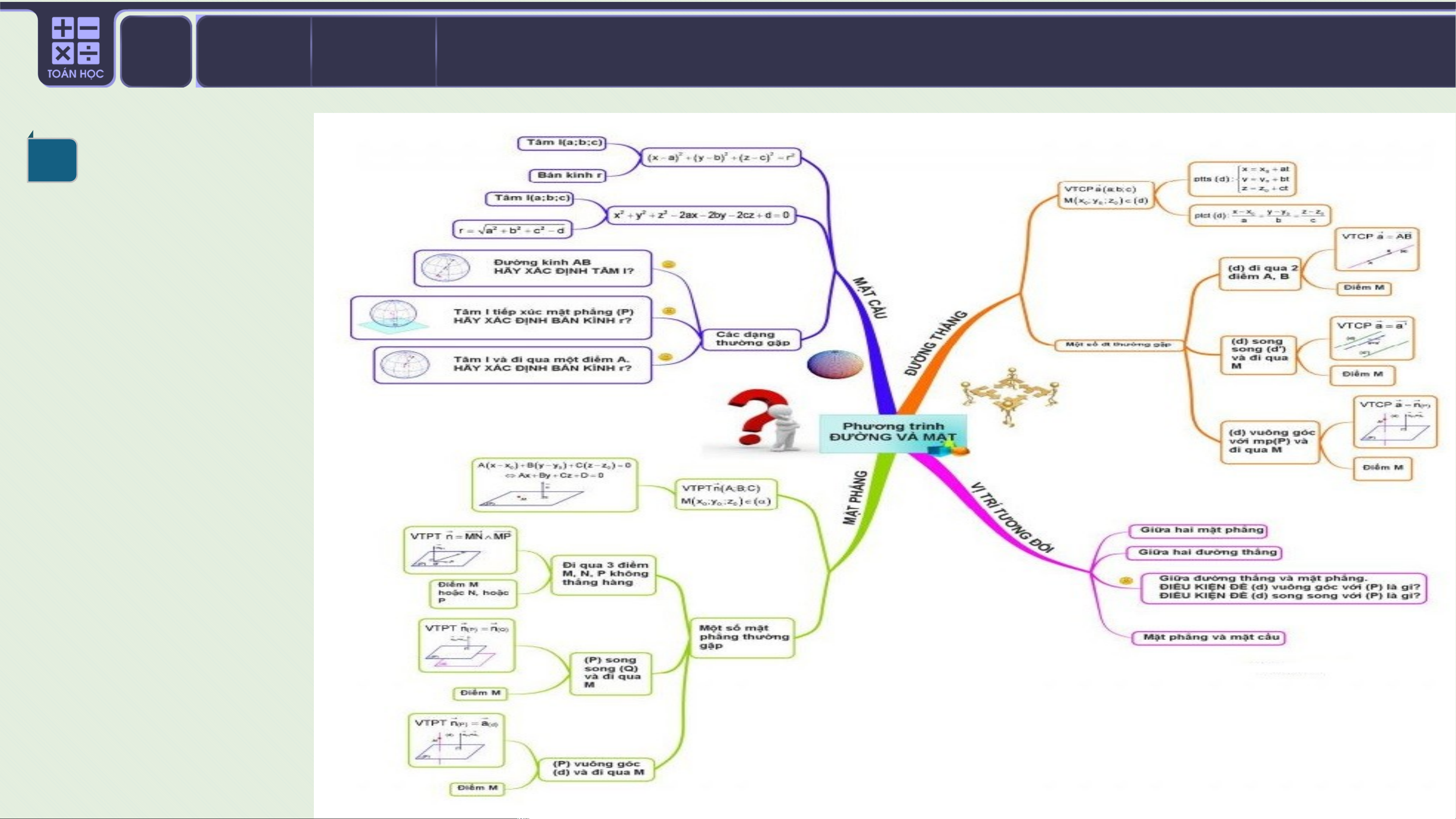
HỆ THỐNG KIẾN THỨC
I
GIÁO ÁN ĐIỆN TỬ - DIỄN ĐÀN GIÁO VIÊN TOÁN
TOÁN
LỚP
12 THPT
CÁC VÍ DỤ MINH HỌA
II
Ví dụ 1:
Bài giải
Trong không gian với hệ tọa độ , cho ; , và các điểm . Tính góc giữa hai véc tơ , .
Ta có ;
cos
(
𝐴𝐵,
𝑀𝑁
)
=
𝐴𝐵.
𝑀𝑁
|
𝐴𝐵
|
.
|
𝑀𝑁
|
=
⇒
(
𝐴𝐵 ,
𝑀𝑁
)
=13 5
𝑜
GIÁO ÁN ĐIỆN TỬ - DIỄN ĐÀN GIÁO VIÊN TOÁN
TOÁN
LỚP
12 THPT
CÁC VÍ DỤ MINH HỌA
II
Ví dụ 2:
Bài giải
Trong không gian ,cho điểm . Gọi lần lượt là hình chiếu của trên trục và trên mặt
phẳng . Viết phương trình mặt trung trực của đoạn .
là hình chiếu của trên trục nên ta có .
là hình chiếu của trên mặt phẳng nên ta có .
Gọi là trung điểm . Ta có .
Mặt phẳng trung trực (P) của đoạn đi qua và có VTPT
Phương trình (P) : .
GIÁO ÁN ĐIỆN TỬ - DIỄN ĐÀN GIÁO VIÊN TOÁN
TOÁN
LỚP
12 THPT
CÁC VÍ DỤ MINH HỌA
II
Ví dụ 3:
Bài giải
Trong không gian với hệ tọa độ cho điểm , , .
a) Tìm tọa độ điểm thỏa mãn .
b) Tìm tọa độ điểm N trên trục sao cho: nhỏ nhất.
c) Gọi là điểm trên mặt phẳng thỏa mãn nhỏ nhất.
a) Gọi , ta có ;
𝐼𝐴 −
𝐼𝐵+
𝐼𝐶=
0
𝐼𝐶=
(
2−𝑥; − 3−𝑦;1−𝑧
)
⇔
{
1+2−𝑥=0
−4−3−𝑦=0
2+1−𝑧=0
. Vậy