HÌNH HỌC
Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG
GIAN
LỚP
12
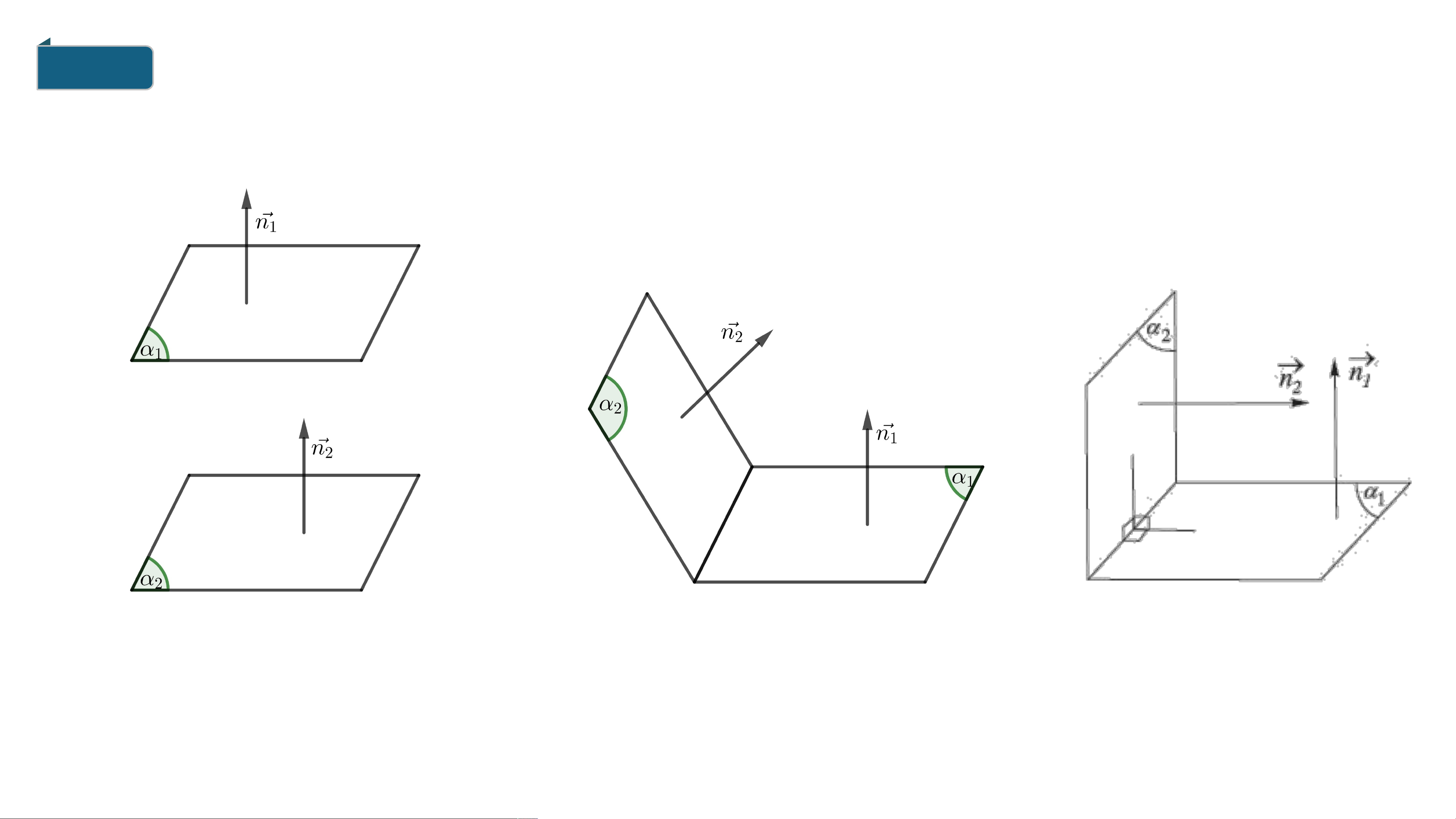
ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG
SONG, VUÔNG GÓC
III
Bài 2: PHƯƠNG TRÌNH MẶT PHẲNG (tiết 2)
BÀI TẬP TRẮC NGHIỆM
ĐIỀU KIỆN ĐỂ HAI MẶT PHẲNG SONG SONG, VUÔNG
GÓC
1. Lý thuyết
III
//
Ví dụ 1:
Bài giải
Cho hai m t ph ng và có ph ng trìnhặ ẳ ươ
Có nh n xét gì v vector pháp tuy n c a chúng?ậ ề ế ủ
2. Các ví dụ minh họa
=(1;-2;3)
=(2;-4;6)=2(1;-2;3)
Ví dụ 2:
Bài giải
Vi t ph ng trình m t ph ng đi qua đi m M(1;-2;3) và ế ươ ặ ẳ ể
song song v i m t ph ng ớ ặ ẳ
Vì m t ph ng song song v i m t ph ng nên có vector pháp tuy n ặ ẳ ớ ặ ẳ ế =(2;-
3;1). Mặt phẳng đi qua điểm M(1;-2;3), vậy có phương trình:
hay
2. Các ví dụ minh họa
2. Các ví dụ minh họa
Ví dụ 3:
Bài giải
Vi t ph ng trình m t ph ng đi qua hai đi m A(3;1;-1), B(2;-1;4) và vuông ế ươ ặ ẳ ể
góc v i m t ph ng có ph ng trình: ớ ặ ẳ ươ
G i là vector pháp tuy n c a m t ph ng . Hai vector không cùng ph ng có giá ọ ế ủ ặ ẳ ươ
song song ho c n m trên là: ặ ằ
Do đó m t ph ng có vector pháp tuy n: ặ ẳ ế
V y ph ng trình c a là: ậ ươ ủ
Hay