CHƯƠNG IV:
PHỤ THUỘC HÀM
I. Giới thiệu
¡Functional Dependency
¡Phụ thuộc hàm là khái niệm được xây
dựng để mô tả các ràng buộc logic
trong CSDL
-là công cụ để biểu diễn các ràng buộc logic
giữa các thuộc tính của quan hệ
8/9/21 8:06 AM 2
8/9/21 8:06 AM 3
*Định nghĩa PTH
¡Cho quan hệ R(U), trong đó U = {A1, A2,…An} là tập thuộc tính.
Cho X,Y là tập thuộc tính con thuộc U
¡Nói rằng Xxác định hàm Yhay Yphụ thuộc hàm vào X, ký
hiệu X®Y, nếu với mọi quan hệ (bộ) rxác định trên R(U) và với
hai bộ t1và t2bất kỳ mà t1[X] = t2[X] thì t1[Y] = t2[Y]
¡Cách đọc khác:Xxác định duy nhất Y(hay Xkéo theo Y)
-Xgọi là vế trái của PTH, Ylà vế phải acủa PTH
¡Ký hiệu: F:= { f : Lj →Rj |Lj, Rj
⊆
Ω } là tập các
phụ thuộc hàm trên các thuộc tính Ω
¡Ví dụ:
HOADON (soHD,NgayLap, TongGiaTri)
CHITIET_HOADON (SoHD,MaHang,SoLuong, DonGia, ThanhTien)
-SoHD ®NgayLap
-SoHD ®TongGiaTri
-SoHD, MaHang ®SoLuong
-SoHD, MaHang ®DonGia
-SoHD, MaHang ®ThanhTien
8/9/21 8:06 AM 4
8/9/21 8:06 AM 9
¡Biểu diễn phụ thuộc hàm:
-Liệt kê các thuộc tính, dùng đường nối mũi tên từ các thuộc tính vế
trái đến các thuộc tính vế phải của tất cả các phụ thuộc hàm
¡Ví dụ:
MƯỢN(Sốthẻ, Mãsốsách, Tênngườimượn, Tênsách, Ngàymượn )
-Với các phụ thuộc hàm:
FD1:Sốthẻ ®Tênngườimượn
FD2:Mãsốsách ®Tênsách
FD3:Sốthẻ, Mãsốsách ®Ngàymượn
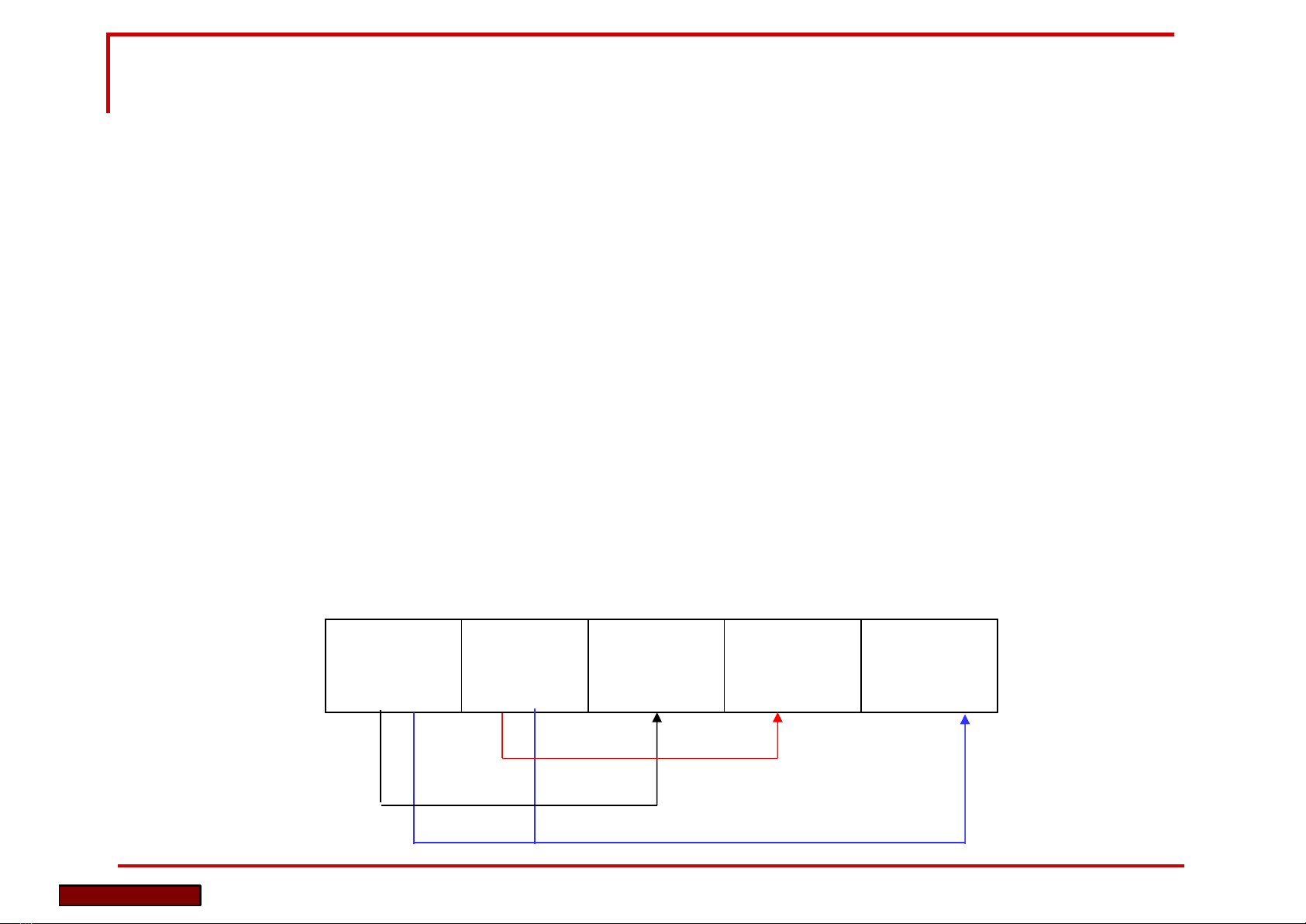
¡Có sơ đồ phụ thuộc hàm như sau:
Sốthẻ Mã số
sách
Tên người
mượn Tên sách Ngàymượn
FD3
FD1
FD2