Bài giảng Nguyên lý thị giác – Ngành Truyền thông Đa phương tiện
38
Bộ môn Truyền thông Đa phương tiện – Đại học Công nghệ thông tin và Truyền thông
Tranh những người mót lúa, 1857. Tranh sơn dầu của Mi-lê
Chƣơng 3: Biểu hiện không gian trên mặt phẳng – các phép chiếu
Nghiên cứu về không gian là quá trình lao động sáng tạo không ngừng của con người.
Đối với việc tạo dựng không gian, các nhà khoa học đã phát minh ra nhiều công cụ để ghi
chép không gian một cách nhanh chóng và chính xác như ống kính máy ảnh, máy quay
phim…
Trong hội họa cũng vậy, từ lâu người ta đã tìm ra nhiều phương pháp để biểu đạt
không gian: mầu sắc, sáng tối, đậm nhạt, hoặc bằng đường nét kết hợp mầu sắc. Khác với
các ngành khoa học kỹ thuật khác, không gian trong hội họa là một thứ không gian ảo,
được tái hiện lại trên mặt phẳng.
Để thực hiện được điều này người ta dựa vào nguyên tắc của các phép chiếu hình học, tức là
phép chiếu in hình của vật thể lên mặt phẳng bằng các đường chiếu hình học nhằm tìm kiếm cấu
tạo tương ứng với hình dạng cấu trúc của vật thể ở không gian.
Trên thực tế có ba phép chiếu thông dụng, đó là:
- Phép chiếu song song
- Phép chiếu vuông góc
- Phép chiếu xuyên tâm.
Khái niệm phép chiếu :
- Giả sử ta có mặt phẳng Л
- Một điểm S
- Một điểm A bất kỳ
- Dựng đường AS cắt Л tại điểm A = Ta đã thực hiện một phép chiếu.
Bài giảng Nguyên lý thị giác – Ngành Truyền thông Đa phương tiện
39
Bộ môn Truyền thông Đa phương tiện – Đại học Công nghệ thông tin và Truyền thông
3.1. Phép chiếu song song:
Là phép chiếu mà các tia chiếu thì song song với nhau và song song với phương chiếu.
Biểu diễn lại phép chiếu song song
- Cho một mặt phẳng Л: gọi là mặt phẳng hình chiếu
- Một đường thẳng S không song song với Л: gọi là hướng chiếu
- Giả thiết, có một điểm A bất kì trong không gian. Qua A vạch đường thẳng AA song
song với S: gọi là tia chiếu qua A.
Đường thẳng AA cắt mặt phẳng hình chiếu Л ở điểm A : goi là hình chiếu song song của
A lên mặt phẳng hình chiếu Л.
Nếu có một hình (H), thì tập hợp các hình chiếu song song của các điểm thuộc (H) sẽ cho
hình (H ) gọi là hình chiếu song song của (H)
Trường hợp nếu hướng chiếu S thẳng góc với mặt phẳng Л thì phép chiếu song song được
gọi là phép chiếu vuông góc.
Trường hợp nếu ta cho các đường thẳng song song là các đường sẽ cắt nhau ở điểm vô tận
thì phép chiếu song song là trường hợp đặc biệt của phép chiếu xuyên tâm khi tâm chiếu ở
vô tận.
Những bóng ngả của đồ vật in lên tường hay lên mặt đất khi trời nắng cho ta hình dung kết
quả của phép chiếu song song
Áp dụng phép chiếu này, ta có thể biểu hiện được hình khối của sự vật một cách ước lệ,
tức là gây được sự nổi và chiều sâu nhưng không gây được ấn tượng thật về không gian
như mắt ta vẫn thường thấy.
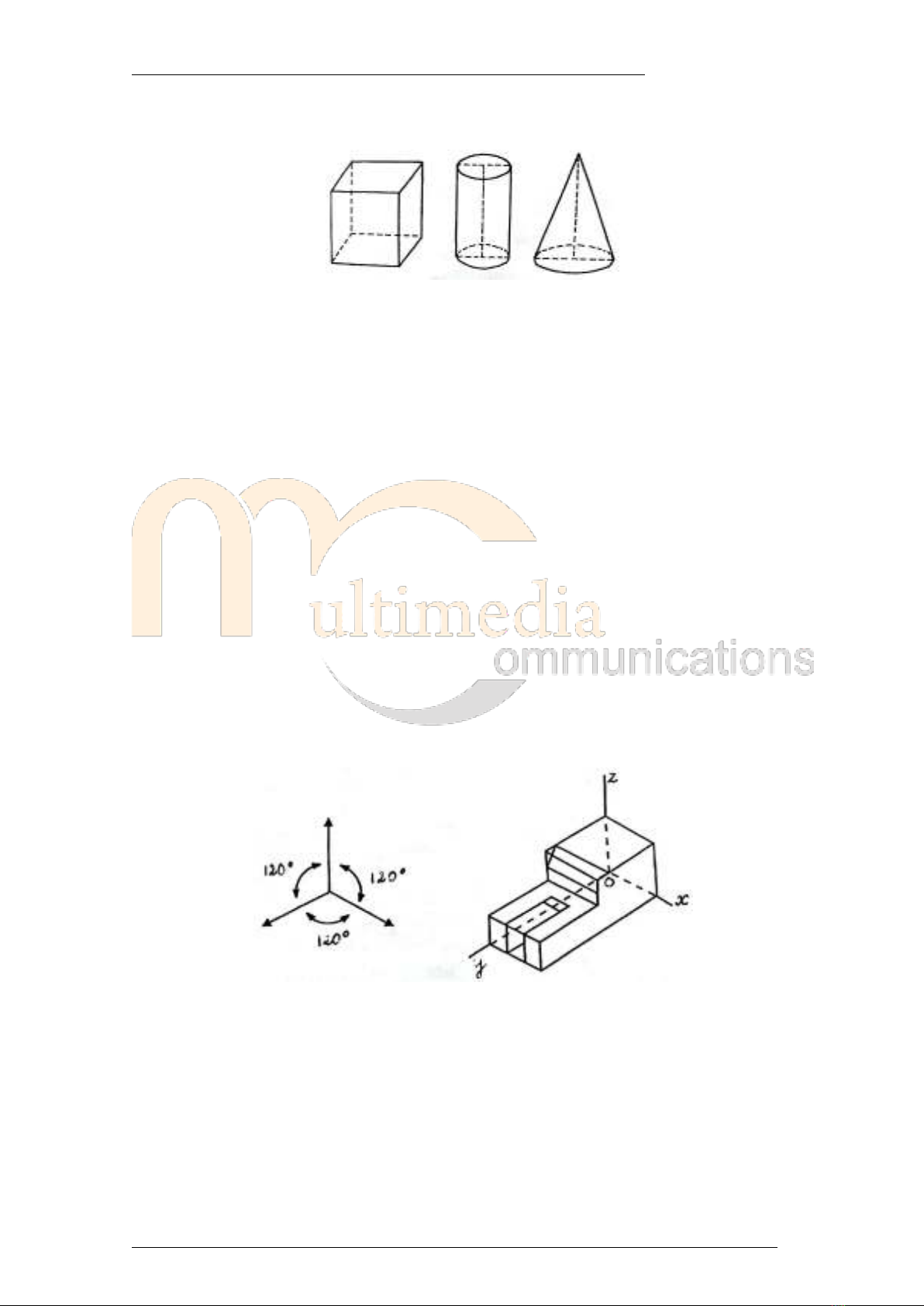
Theo phép chiếu song song thì những hình đi vào chiều sâu đều biến dạng theo một quy ước:
Hình chữ nhật trở thành hình bình hành, hình tròn trở thành hình elip…như ta vẫn thường thấy
trong hình học không gian.
Bài giảng Nguyên lý thị giác – Ngành Truyền thông Đa phương tiện
40
Bộ môn Truyền thông Đa phương tiện – Đại học Công nghệ thông tin và Truyền thông
Trong những bản vẽ kỹ thuật và xây dựng người ta thường trình bày theo một thể loại để
người đọc bản vẽ dễ dàng hình dung ra được vật thể gọi là: Hình chiếu trục đo.
Để thực hiện được người ta gắn vật thể vào một hệ trục Ox, Oy, Oz trong đó có một trục
thẳng đứng và hai trục kia làm thành góc với nó theo những góc độ quy định, rồi kẻ từ các
điểm mốc của vật thể những đường song song với ba trục đó để có các cạnh và các mặt
theo ba chiều, cuối cùng được phối cảnh của vật thể.
Có 3 loại hình chiếu trục đo thường dùng, mà tên gọi căn cứ vào các góc độ của hệ trục.
3.1.1. Hình chiếu trục đo thẳng góc đẳng trắc
Đẳng: Thứ bậc, Ngang bằng nhau
Trắc: Thương xót – Trắc ẩn. Chật hẹp – Trắc trở. Đo sâu cạn – Trắc địa
= Đẳng trắc: Đo trong trường hợp các góc bằng nhau
Ba trục Ox. Oy, Oz làm với nhau những góc bằng nhau và đều bằng 120°, (Một góc 360°/3
= 120°) loại này dễ vẽ, ít gây nhầm lẫn và đẹp mắt, nhưng với những vật thể vuông vắn thì
hình biểu diễn lại xấu và có vẻ dị dạng.
3.1.2. Hình chiếu trục đo thẳng góc nhị trắc
Nhị: Hai
Trắc: Thương xót – Trắc ẩn. Chật hẹp – Trắc trở. Đo sâu cạn – Trắc địa
=> Nhị trắc: Đo hai góc
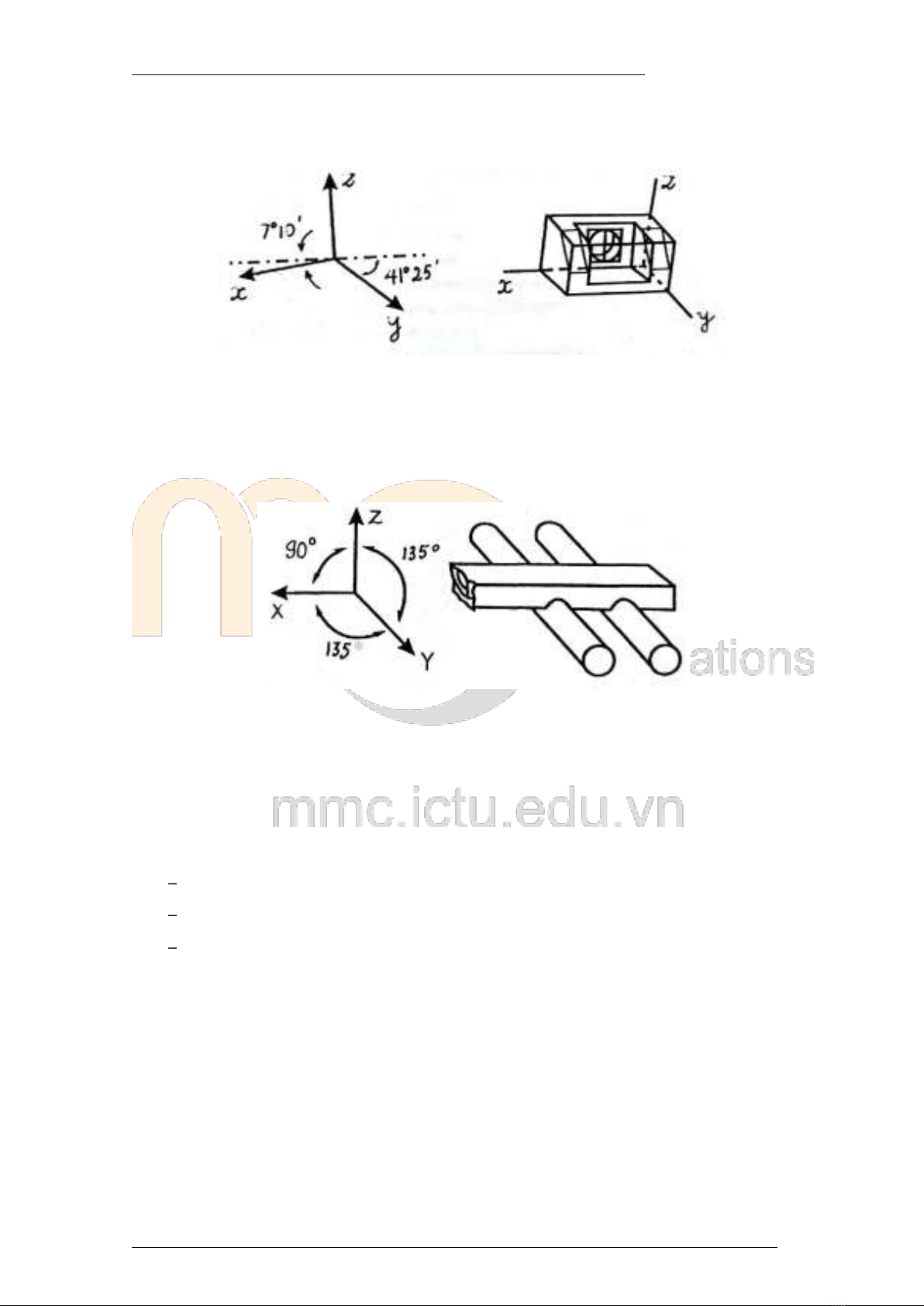
Hệ trục gồm một trục thẳng đứng và hai trục kia nghiêng với đường nằm ngang những góc
7°10 và 41°25 . Với những góc độ như vậy, hình chiếu sẽ cho cảm giác thuận mắt, tránh
Bài giảng Nguyên lý thị giác – Ngành Truyền thông Đa phương tiện
41
Bộ môn Truyền thông Đa phương tiện – Đại học Công nghệ thông tin và Truyền thông
tình trạng chập nét, thường thích hợp cho những hình vuông vắn và những vật thể có nhiều
chi tiết
3.1.3. Hình chiếu trục đo xiên góc nhị trắc
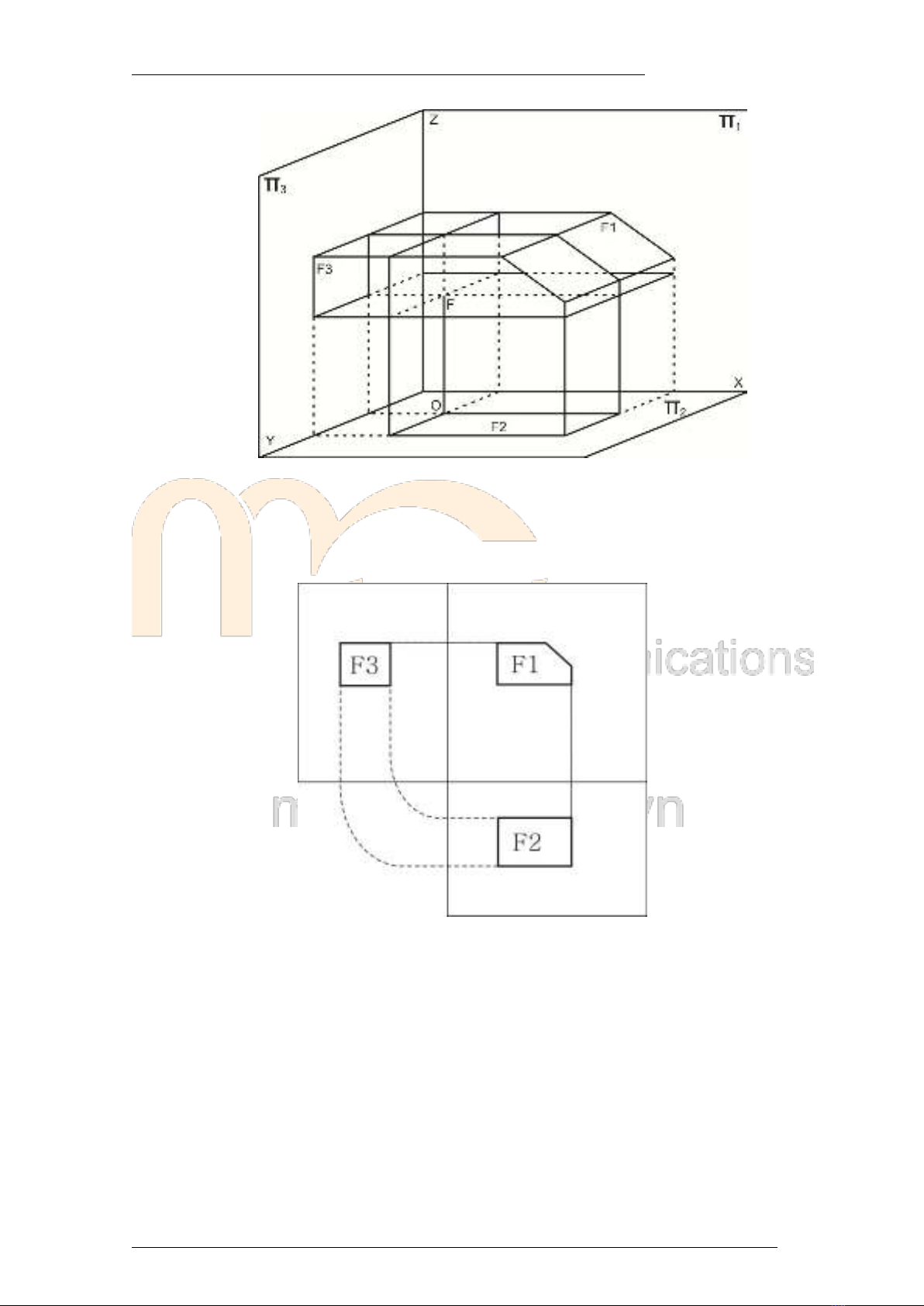
Hệ trục gồm một trục thẳng đứng, một trục nằm ngang và trục thứ ba nghiêng một góc 45°
với đường nằm ngang. Loại này cũng dễ vẽ và thích hợp với những vật thể có nhiều hình
tròn hướng về phía trước.
3.2. Phép chiếu vuông góc
Khái niệm: Là phép chiếu mà các tia chiếu thì song song với nhau và song song với
phương chiếu S, mà S vuông góc với mặt phẳng hình chiếu
Phƣơng pháp: Trong phép chiếu vuông góc, người ta quy ước hệ thống mặt chiếu là ba
mặt phẳng vuông góc với nhau:
Mặt chiếu Л1 thẳng đứng, gọi là mặt chiếu đứng.
Mặt chiếu Л2 nằm ngang, gọi là mạt chiếu bằng
Mặt chiếu Л3 vuông góc với 2 mặt phẳng kia tức là vuông góc với giao tuyến của
chúng, gọi là mặt chiếu cạnh.
Bài giảng Nguyên lý thị giác – Ngành Truyền thông Đa phương tiện
42
Bộ môn Truyền thông Đa phương tiện – Đại học Công nghệ thông tin và Truyền thông
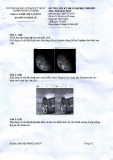
Hình 38a
Nếu từ những điểm của hình F kẻ những đường thẳng góc xuống các mặt phẳng hình chiếu
đó, ta được những hình F1, F2, F3 của F theo 3 mặt: mặt bằng, mặt đứng, mặt cạnh.
Hình 38b
Trên ví dụ 38b, 3 mặt chiếu theo các trục Ox, Oy, Oz hợp thành 1 hệ thống trục, cho ta
hình dung được 3 chiều củ vật thể: trục Ox chỉ chiều rộng, trục Oy chỉ chiều sâu, trục Oz
chỉ chiều cao.
Đem dàn những hình này trên một mặt phẳng, ta được một bản vẽ trình bày cấu trúc của F
theo đúng kích thước của nó. Nhìn vào bản vẽ ta có thể nhận xét vật thể một cách tường
tận về kích thước, hình dáng theo nhiều phía. Nếu bản vẽ biểu diễn thêm mặt cắt thì ta còn
