
SỨC BỀN VẬT LIỆU 1
CHƯƠNG 4
TRẠNG THÁI ỨNG SUẤT VÀ CÁC THUYẾT BỀN
1. TÓM TẮT LÝ THUYẾT
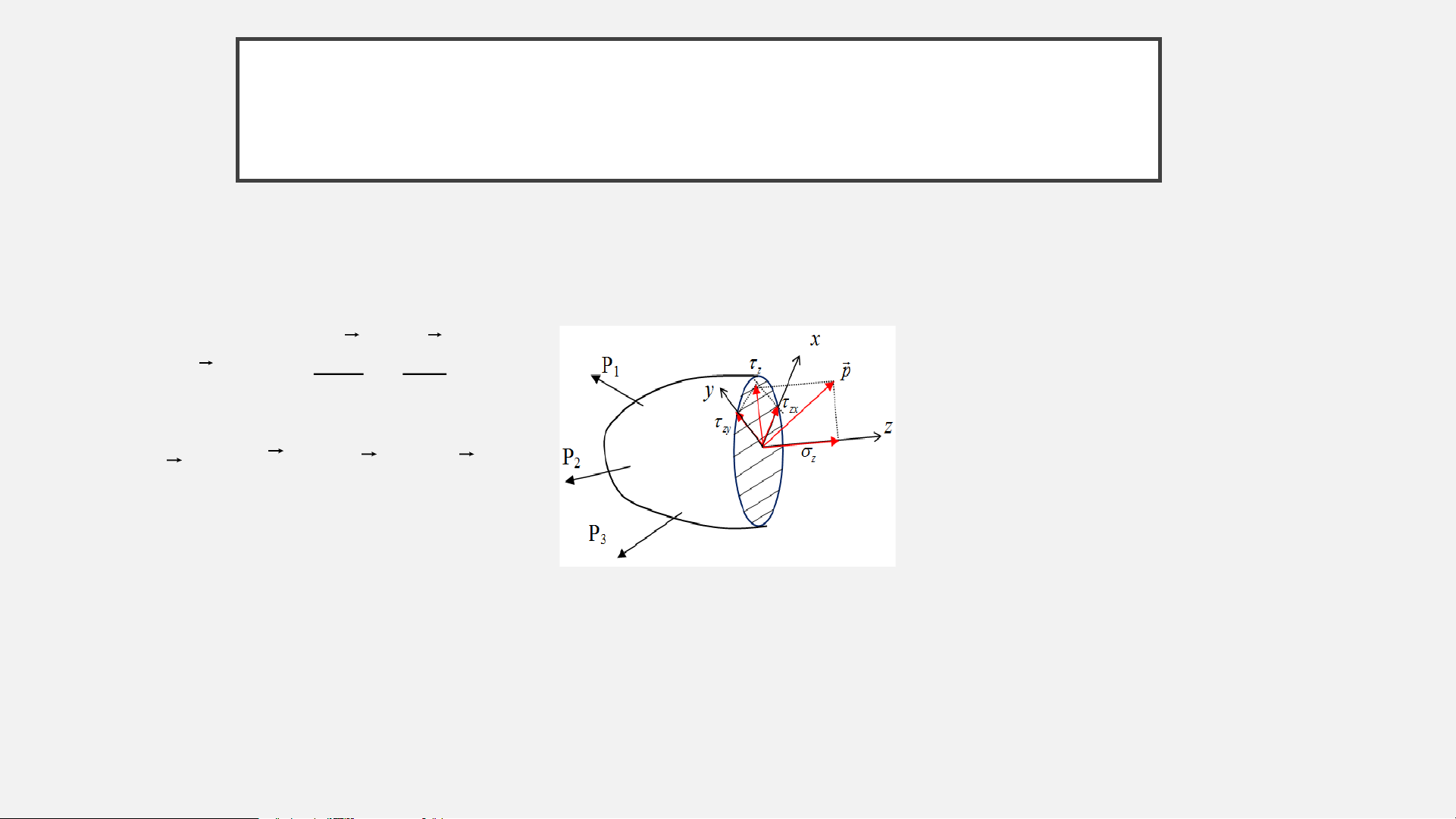
1. Khái niệm về trạng thái ứng suất
Ứng suất toàn phần tại 1 điểm K trên tiết diện có pháp tuyến n là:
0
lim
F
P dP
pF dF
→
==
. . .
z zx zy
p k i j
= + +
1. TÓM TẮT LÝ THUYẾT
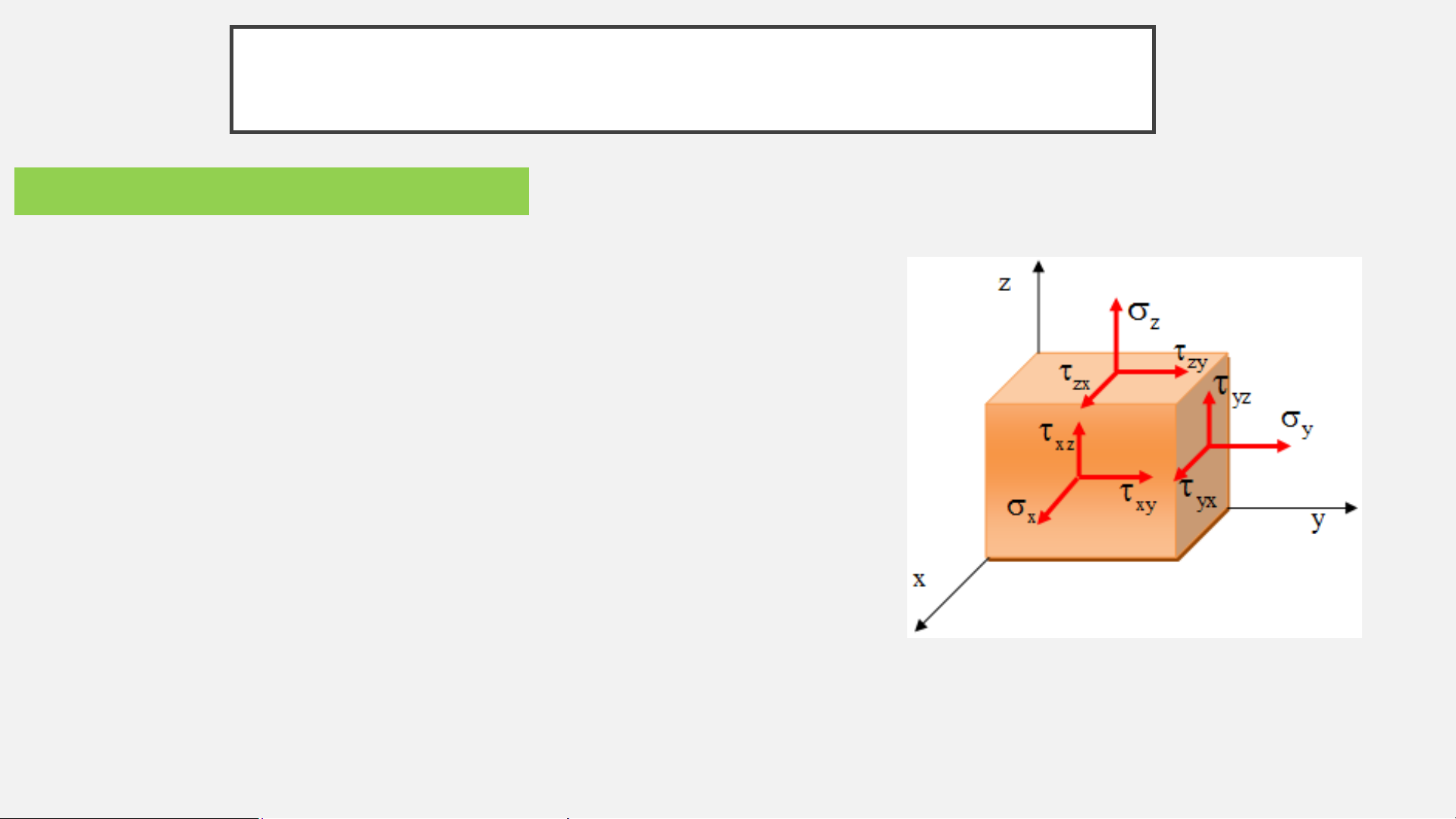
1. Khái niệm về trạng thái ứng suất
-Tại điểm K trong vật thể tách ra một phân tố hình hộp có kích
thước vô cùng bé bao quanh K
-Trạng thái ứng suất(TTUS)
tại một điểm K của vật thể đàn hồi
chịu lực là tập hợp tất cả các ứng suất tác dụng trên các mặt vô
cùng bé đi qua điểm đó
Đặc trưng bởi Ten xơ ứng suất có 6 thành phần độc lập
x yx zx
xy y zy
xz yz z
σ τ τ
τ σ τ
τ τ σ
=
T
σx, σy, σz
τxy=τyx,τyz=τzy,τzx=τxz
Ứng suất pháp:
Ứng suất tiếp
Định luật đối ứng của ứng suất tiếp
1. TÓM TẮT LÝ THUYẾT
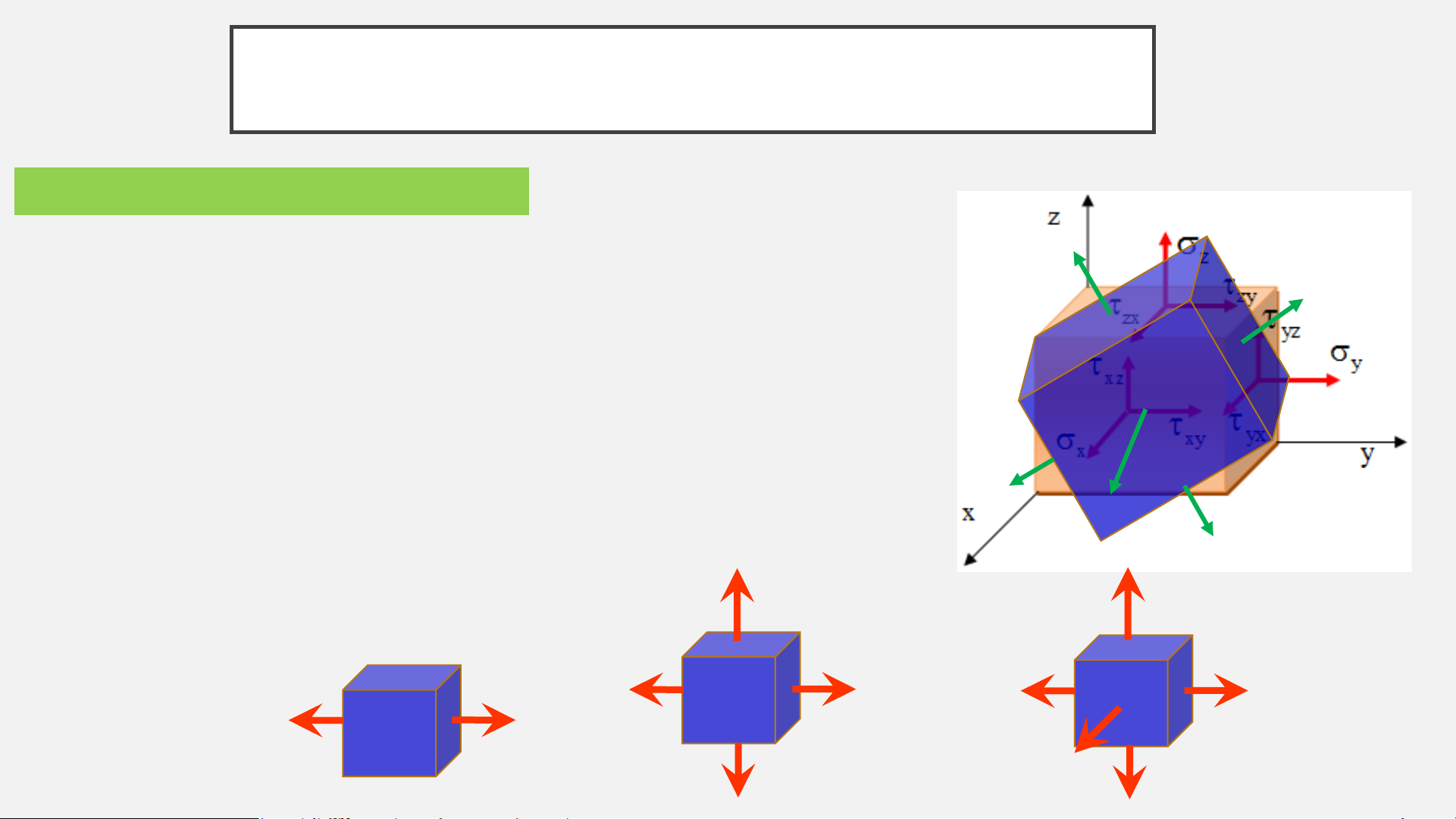
1. Khái niệm về trạng thái ứng suất
-
Mặt chính
: tại 1 điểm ta luôn tìm được 1 phân tố mà trên các mặt
chỉ có ứng suất pháp. Mặt đó gọi là mặt chính
𝜎1> 𝜎2> 𝜎3
Kí hiệu:
- Phương chính là phương của ứng suất pháp
- Lúc đó ứng suất pháp được gọi là ứng suất chính
Phân loại:
•
TTUS khối: 3 ứng suất chính #0
•
TTUS phẳng: 2 ứng suất chính #0
•
TTUS đơn: chỉ có 1 ứng suất chính # 0
1. TÓM TẮT LÝ THUYẾT
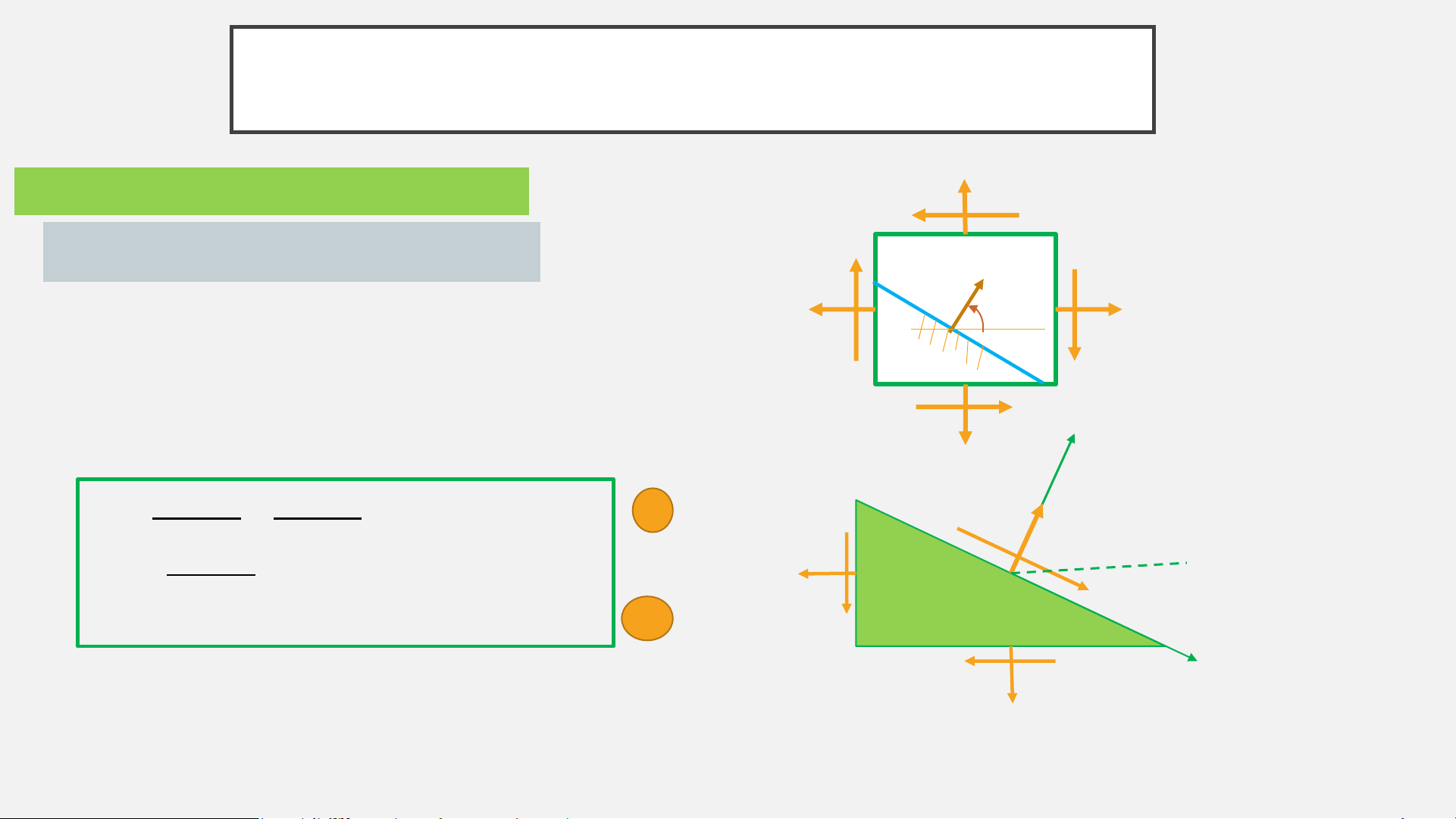
2. Trạng thái ứng suất phẳng
a) Ứng suất trên mặt cắt nghiêng bất kỳ
Xác định ứng suất trên 1 mặt cắt nghiêng bất kỳ và có pháp
tuyến
u
tạo với trục
x
một góc
θ
Tách ra một phân tố , giả sử mặt vuông góc trục z là mặt
chính (σz=0)
σy
σx
σx
σy
τ
yx
τ
xy
τ
xy
τ
yx
θ
u
𝜎𝑢=𝜎𝑥+ 𝜎𝑦
2+𝜎𝑥− 𝜎𝑦
2𝑐os2𝜃 − 𝜏xy sin 2 𝜃
𝜏uv =𝜎𝑥− 𝜎𝑦
2sin 2 𝜃 + 𝜏xy𝑐os2𝜃
σy
τ
yx
σx
τ
xy
σu
τ
uv
u
v
1
2
v


























