Trường Đại học Công nghiệp thành phố Hồ Chí Minh
Khoa Công nghệ Cơ khí
CHƯƠNG 11:
ỨNG DỤNG MATLAB GIẢI CÁC BÀI
TOÁN TỐI ƯU HÓA
Thời lượng: 3 tiết
2
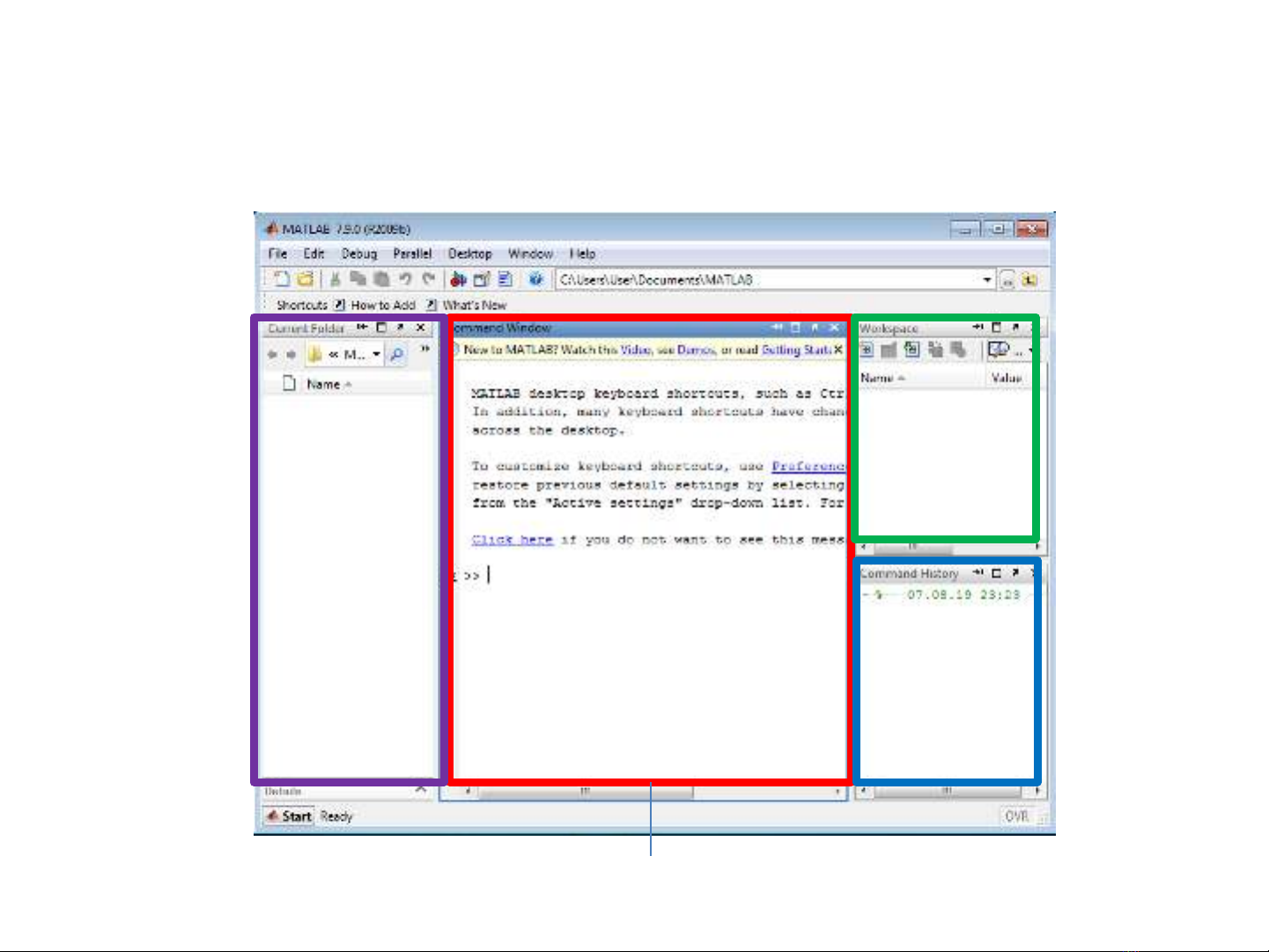
Thống nhất phiên bản MATLAB
Trường câu lệnh
Các biến
tính toán
xong
Trường lịch
sử các câu
lệnh đã
dùng
Chọn thư
mục làm
việc
3
Làm quen với MATLAB
Dấu >>
Ký tự nhắc mặc định trong MATLAB, đầu câu lệnh
>>
Dấu ;
Dấu chấm phẩy ở cuối dòng sẽ tránh việc in kết quả ra trường
câu lệnh (khi ta không cần in kết quả ra cho cửa sổ ngắn gọn)
>> a=2;
Dấu …
Dấu ba chấm ở cuối dòng cho phép tiếp tục code ở dòng tiếp
theo
>> a=…
2
help
tên_câu_lệnh
Hiển thị các thông tin chi tiết về câu lệnh mà người dùng cần
sử dụng
>>help linprog
Chữ cái viết thường và viết hoa được phân biệt khác nhau trong MATLAB
>> a=2
>>A=2
>>A+a
MATLAB coi tất cả các biến đều ở dạng mảng (arrays)
Tên biến
Trong MATLAB tên biến được bắt đầu từ chữ cái và có chiều
dài tối đa 31 ký tự bao gồm chữ cái (in hoa và viết thường là
khác nhau), số và dấu gạch dưới
>>A_a_bc_9=12
Các phép
toán thông
dụng
+
-
*
/
^
>>2+3*6^2/4-7
Tránh trùng
với các tên
biến tích hợp
của hệ thống,
như các hằng
số, tên hàm
pi
sin
cos
v.v..
>>pi
4
Ma trận trong MATLAB
Đối tượng Cách thực hiện Ví dụ
Véc
tơ hàng
Ngoặc
vuông, Dấu cách
A=[1
2 3 4]
Véc
tơ cột
Cách
1: Ngoặc vuông và xuống dòng
B
=[5
2
]
Cách
2: Ngoặc vuông và dấu chấm phẩy
B=[5;2;3]
Cách
3: Đảo véc tơ hàng thành cột bằng dấu
‘
B=[5 2 3]'
Ma
trận [mxn]
Cách
1: áp dụng véc tơ hàng và cột: dấu cách
và
xuống dòng
A=[1
2 3
4 5 6
7 8 9]
Cách
2: Dấu cách và dấu chấm phẩy
A=[1
2 3;4 5 6; 7
8 9]
Ma
trận 1 đơn vị ở
đường
chéo
-
eye(m,n) – ma trận mxn
-
eye(n) – ma trận vuông kích thước n
eye(4)
eye(3,4)
Ma
trận toàn 1
ones(
m,n) hoặc ones(n)
ones(3)
Ma
trận toàn 0
zeros(
m,b) hoặc zeros(n)
zeros(4)
Tạo
ra 1 dãy cấp số
cộng
M:icr:N
M:N
– khi icr=1 theo mặc định
100:
-7:50
50:100
5
Ma trận trong MATLAB (tiếp)
Đối tượng Cách thực hiện Ví dụ
Phần
tử trong ma trận
Dấu
ngoặc tròn:
-
A(i,j) chọn phần tử hàng i, cột j của ma
trận A
-
A(m1:m2,n1:n2) Chọn các phần tử từ
hàng m1 đến hàng m2, cột n1 đến cột n2
A(2,3)
A(2:3,1:3)