CƠ HỌC VẬT RẮN VÀ SÓNG CƠ
SOLID MECHANICS AND MECHANICAL WAVE
TS. NGUYỄN HỮU HÀO
TP. HỒ CHÍ MINH 12-2021
1
PHẦN II – ĐỘNG HỌC
CHƯƠNG 8: HAI CHUYỂN ĐỘNG CƠ BẢN CỦA VẬT RẮN
Slide 2
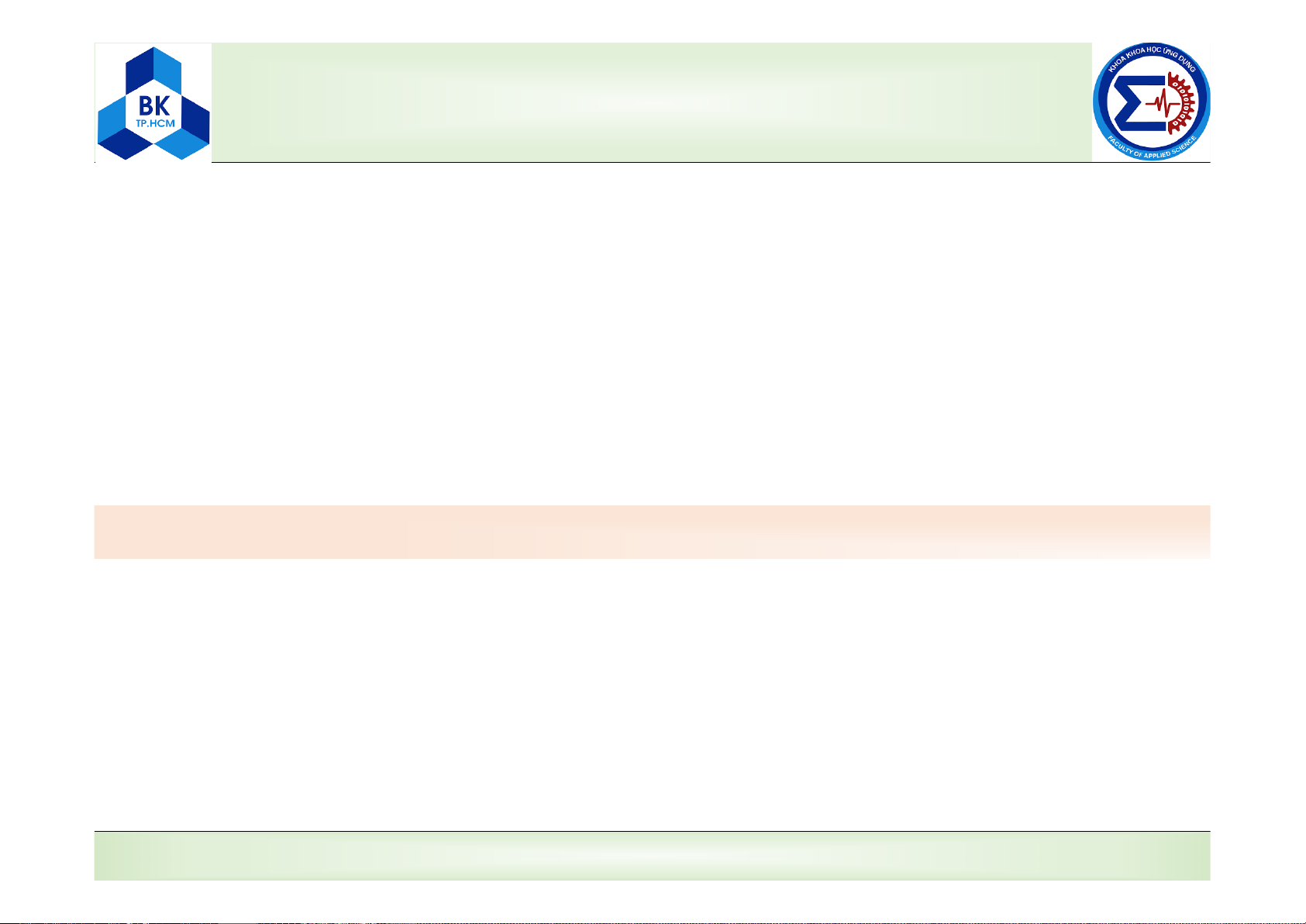
8.1. Chuyển động tịnh tiến của vật rắn
TS. Nguyễn Hữu Hào – 0982243334 Bộ môn Cơ Kỹ Thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa TP. Hồ Chí Minh
Định nghĩa: Là chuyển động mà mỗi đường thuộc vật luôn luôn song song với vị
trí ban đầu của nó.
a) Chuyển động tịnh tiến thẳng b) Chuyển động tịnh tiến cong
PHẦN II – ĐỘNG HỌC
CHƯƠNG 8: HAI CHUYỂN ĐỘNG CƠ BẢN CỦA VẬT RẮN
Slide 3
8.1. Chuyển động tịnh tiến của vật rắn
TS. Nguyễn Hữu Hào – 0982243334 Bộ môn Cơ Kỹ Thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa TP. Hồ Chí Minh
Tính chất của chuyển động tịnh tiến:
• Khi vật rắn chuyển động tịnh tiến thì mọi điểm thuộc vật rắn có cùng quỹ đạo, vận
tốc và gia tốc.
• Quỹ đạo, vận tốc và gia tốc của một điểm bất kỳ thuộc vật rắn cũng chính là quỹ
đạo, vận tốc và gia tốc của vật rắn đó.
/
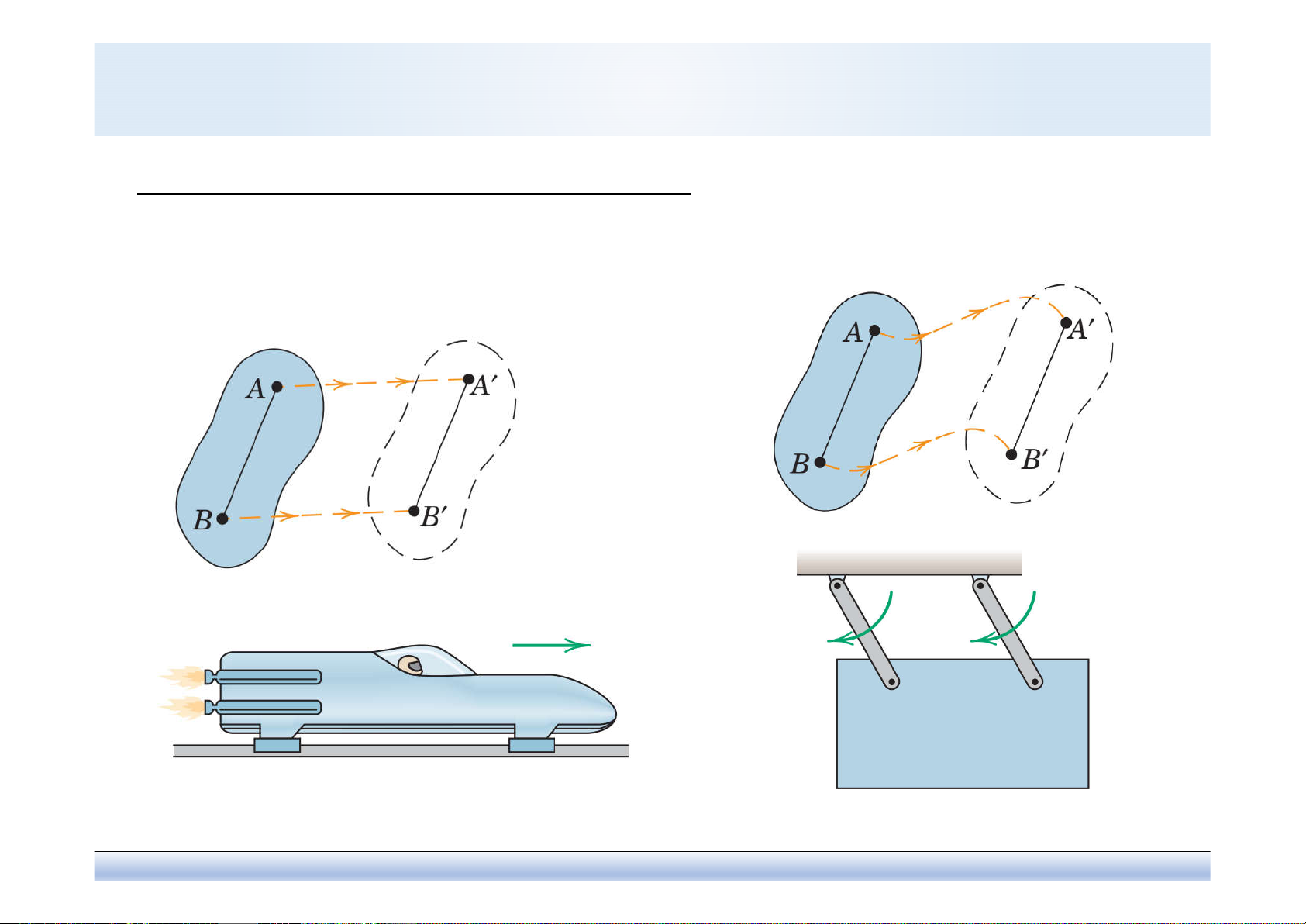
A B A B
r r r
/
A B
r const
Có
Mà
/
A B
r
và
/
A B
r
nên
Do vậy:
A B
r r
và
A B
r r
Hay:
A B
v v
và
A B
a a
A
v
B
v
Chứng minh:
PHẦN II – ĐỘNG HỌC
CHƯƠNG 8: HAI CHUYỂN ĐỘNG CƠ BẢN CỦA VẬT RẮN
Slide 4
8.2. Chuyển động quay của vật rắn
TS. Nguyễn Hữu Hào – 0982243334 Bộ môn Cơ Kỹ Thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa TP. Hồ Chí Minh
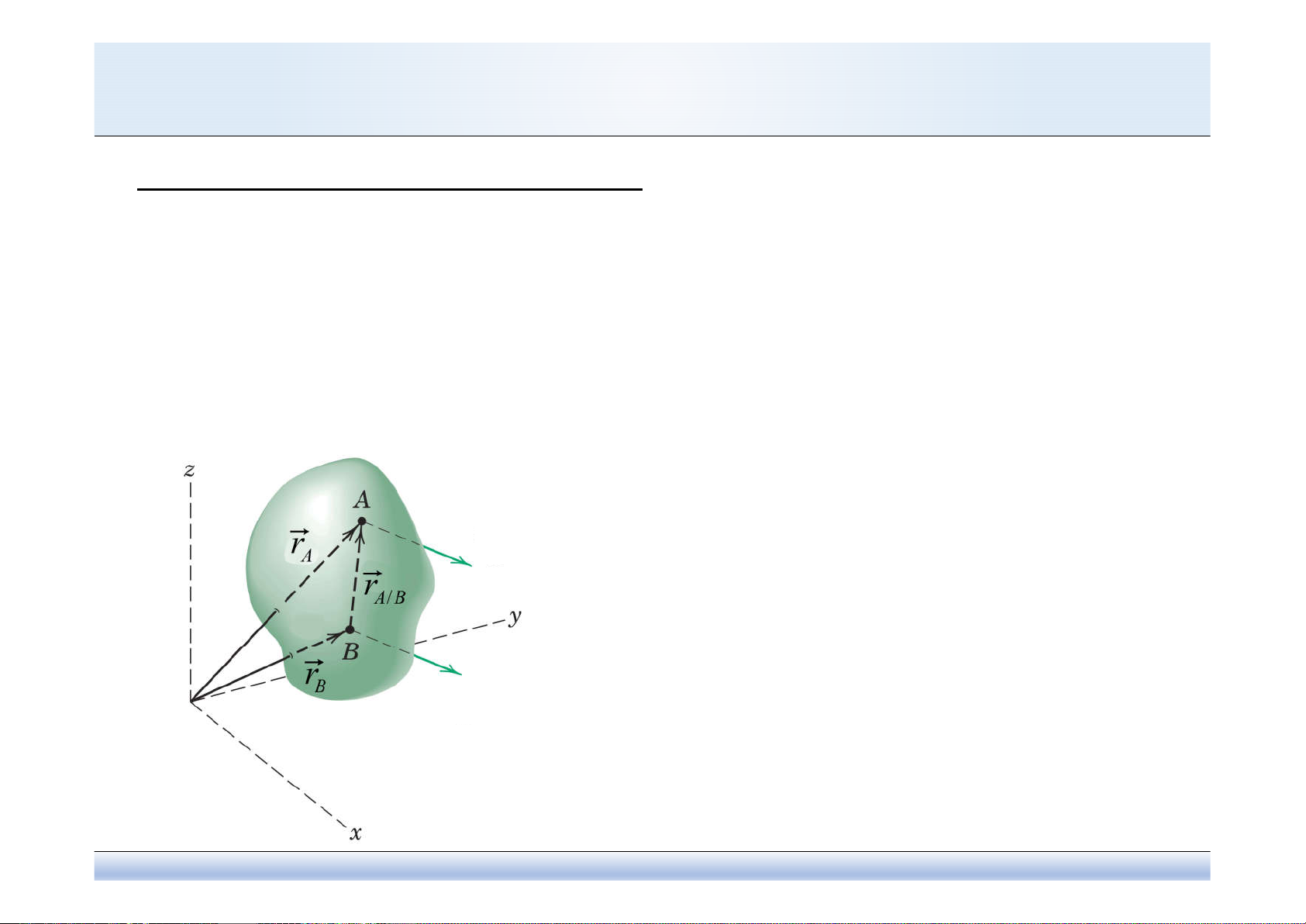
Định nghĩa: Một vật rắn được xem là chuyển động quay khi nó có sự thay đổi
góc quay so với phương tham chiếu ban đầu.
Tính chất: Tất cả các đường thẳng cùng nằm
trong mặt phẳng chuyển động và cùng thuộc
một vật rắn thì có độ dịch chuyển góc quay, vận
tốc góc và gia tốc góc giống nhau.
2 1
Có:
Vì:
const
nên
2 1
2 1
và
Gyroscope dynamic balance
PHẦN II – ĐỘNG HỌC
CHƯƠNG 8: HAI CHUYỂN ĐỘNG CƠ BẢN CỦA VẬT RẮN
Slide 5
TS. Nguyễn Hữu Hào – 0982243334 Bộ môn Cơ Kỹ Thuật – Khoa Khoa học Ứng dụng – Đại học Bách khoa TP. Hồ Chí Minh
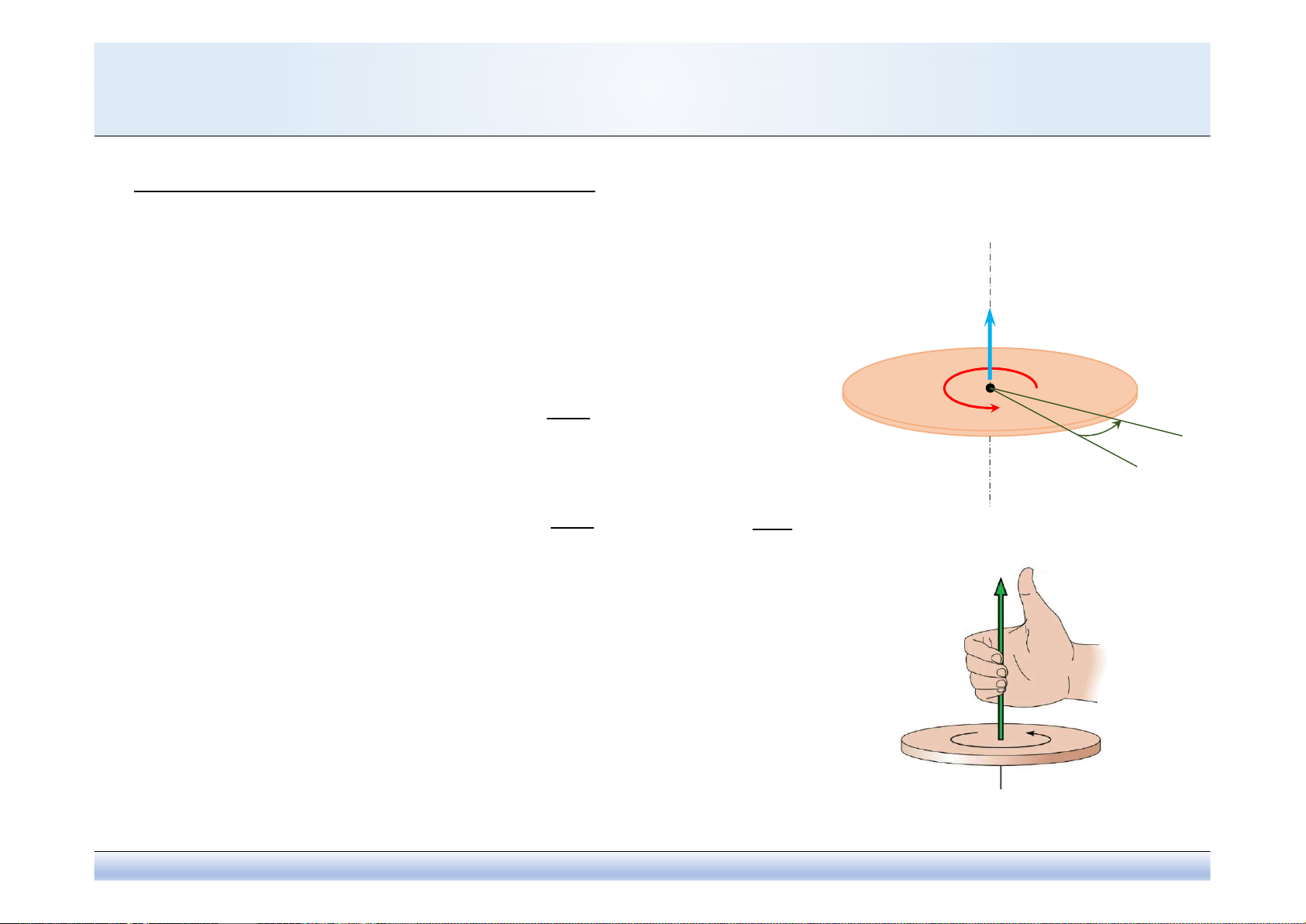
Vận tốc góc của vật:
d
• Giả sử trong thời gian Δt =t1–t0vật rắn
quay được một góc Δθ =θ1–θ0.
• Vận tốc góc trung bình:
av
t
• Vận tốc góc tức thời: 0
lim
t
t
hay
d
dt
• Chiều dương của véc tơ vận tốc góc: Nhìn từ mút
véc-tơ vận tốc góc thấy vật quay ngược chiều kim
đồng hồ.
• Đơn vị vận tốc góc trọng hệ SI: 1/s hoặc rad/s hoặc s-1.
8.2. Chuyển động quay của vật rắn