1
Chương 4
DẦM
Chuyeån vò theo phöông vuoâng goùc truïc
thanh (ñoä voõng):
2 3
1 2 3 4
2 3
1234
1
e e
v x a a x a x a x
x x x a P x a
N N N N q N q
y
v1q
1
1q
2
e
v2q
3
2q
4
L,EJ
x
2 3 2 3
1 3
2 3 2 3
2 2
2 4
2 2
1 3 2 3 2
1 2
vôùi:
x x x x
N N
L L L L
x x x x
N x N x
L L L L
PHẦN TỬ DẦM CHỊU UỐN
2
A' y
B'
B
A
v
x
y
v
x
u=-y
v
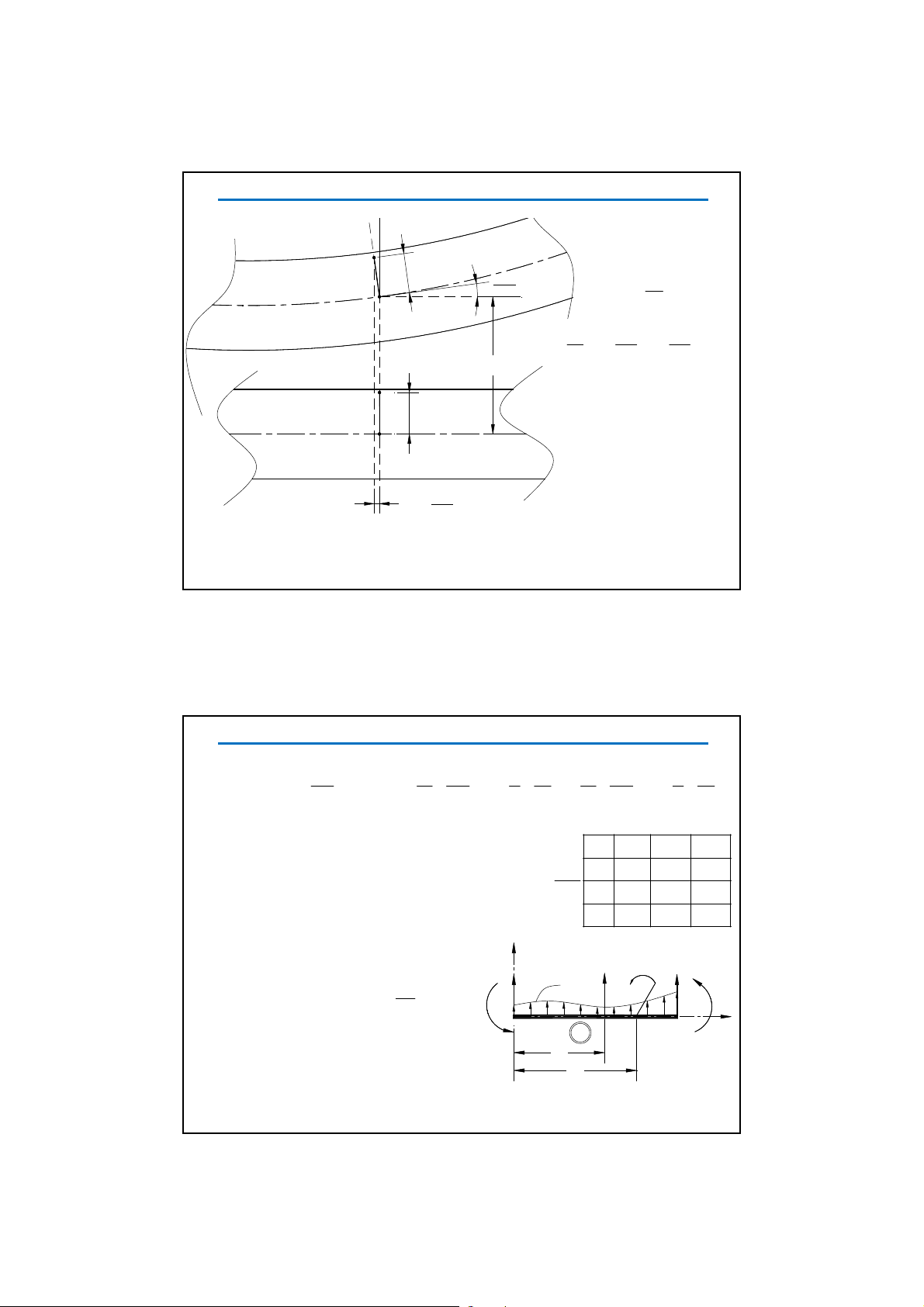
Hình 5: Moâ hình daàm chòu uoán theo Bernuli-Euler
Deã thaáy töø SBVL
(Hình 5)
u y
2 2
2 2
Vaäy: x
e
x
e
du d v d
y y N q
dx dx dx
B q
PHẦN TỬ DẦM CHỊU UỐN
2
2 2 3 2 2 3 2
1 4
6 12 4 6 6 12 2 6
Cuï theå:
d x x x x
B y N y
dx L L L L L L L L
, ,Vôùi daàm chòu uoán: x x
D E
2 2
3
4 1 1 1 1 4
4 4 0
2
12 6 12 6
4 6 2
12 6
4ñx
e
L
T T z
e
V F
L L
L L L
EJ
K B D B dV E B B dFdx
L
L
L
– Ma traän ñoâ cöùng phaàn töû:
– Vectô taûi phaàn töû:
1
0
4 1
1
Q
i
M
i
n
LT
T
Q i
e
i
T
n
M i
i
P N q x dx N x Q
dN
x M
dx
y
P
1
P
2
P
3
P
4
x
x
x
p(x) Q1
e
Q
1
M
1
M1
PHẦN TỬ DẦM CHỊU UỐN
3
Tröôøng hôïp ñaëc bieät:
0
p x const p
2 3
2 3
22 3
0
2
0
2 3
0
2 3
2
2 3
0
2
1 3 2 2
212
3 2 2
12
o
L
e
o
p L
x x
L L
p L
x x
xL L
P p dx
p L
x x
L L
p L
x x
L L
PHẦN TỬ DẦM CHỊU UỐN
Tröôøng hôïp coù löïc taäp trung Qñaët caùch nuùt ñaàu phaàn töû 1 khoaûng a (xQ= a)
2 3
2 3
2 3 1
22
2 3
3
2 3
4
2 3
2
1 3 2
2
3 2
T
e
a a
L L
P
a a
aP
L L
P N a Q Q P
a a
PL L
a a
L L
y
P
1
P
2
P
3
P
4
x
x =a
Q
e
Q
L
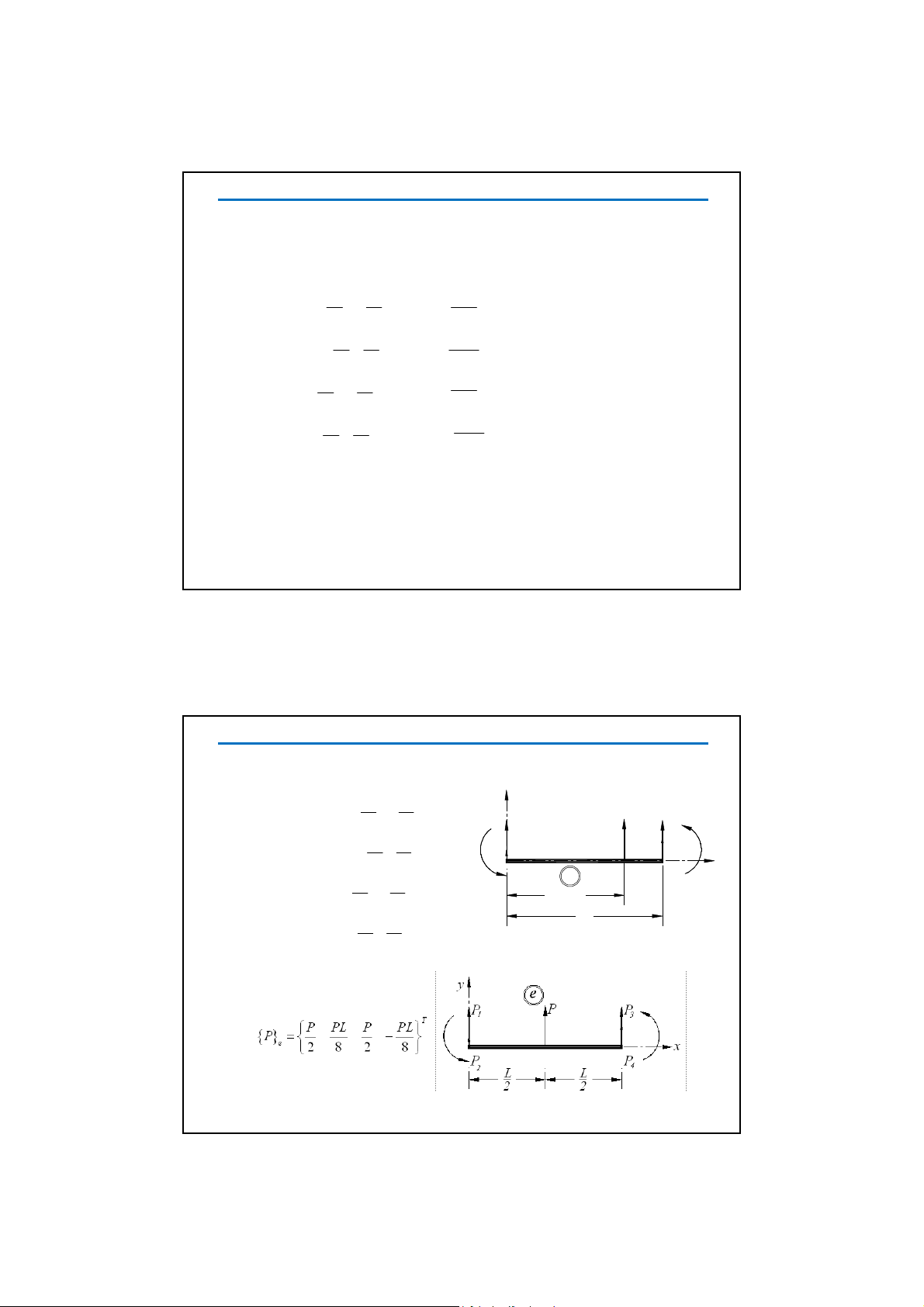
Tröôøng hôïp löïc taäp trung Phöôùng leân vaø ñaët ôû giöõa daàm:
PHẦN TỬ DẦM CHỊU UỐN
4
Xaùc ñònh momen uoán noäi löïc:
2 2
2 2
Baäc I
e e
d v d
M EJ EJ N q EJ N q
dx dx 
1
2
taïi
Goïi: laø vectô momen uoán taïi 2 ñaàu p
haàn töû
taïi
e
M n
MM n
2 1 4 1
2 4
0
thì:
e e e
e
N x
M EJ q S q
N x L
2 2
32 2
6 4 6 2
6 2 6 4
trong ñoù: : ma traän tính momen
e
L L L L
EJ
SLL L L L
Nhaän xeùt:laø momen do chuyeån vò nuùt gaây ra. Ñeå ñaày ñuû hôn
caàn coäng theâm momen uoán noäi löïc do taûi troïng taùc duïng treân phaïm vi phaàn töû (M0)
khi xem taát caû caùc nuùt ñöôïc gaén cöùng.
e
M EJ N q
PHẦN TỬ DẦM CHỊU UỐN