1
Chương 7
TẤM CHỊU UỐN
7.1. GIỚI THIỆU
Tấm: biến dạng uốn. Phức tạp hơn k/c khác.
Hai lý thuyết tấm được sử dụng phổ biến:
lý thuyết tấm kinh điển của Kir
choff (gọi tắt là
tấm Kirchoff).
lý thuyết tấm bậc nhất của Mindlin
(gọi tắt là
tấm Mindlin).
2
7.2. LÝ THUYẾT TẤM KIRCHOFF
Giả thiết cơ bản của lý thuyết uốn tấm Kirchoff: đ
oạn
thẳng vuông góc với mặt trung bình (mặt phẳng chia đ
ôi
chiều cao tấm) vẫn thẳng và vuông góc
với mặt trung
bình sau khi biến dạng.
7.2. LÝ THUYẾT TẤM KIRCHOFF
Hệ quả của giả thiết này là ta đã bỏ qua
các thành phần
biến dạng cắt ngang (
0 xzyz
). Do đ
ó, các thành phần
chuyển vị trong mặt phẳng: u, v và w được biểu diễn nh
ư
sau:
),(),,(
),,(
),,(
0yxwzyxw
y
w
zzyxv
x
w
zzyxu
(7.1)
trong đó, mặt phẳng (0, x, y) là mặt giữa của tấm,
vuông góc với bề mặt tấm ; Các thành phần u, v và w tươ
ng
ứng là chuyển vị theo phương x, phương y và phương z; w
0
là chuyển vị tại mặt trung bình (giả thiết biến dạng màng
:
u0 = v0 = 0).
3
7.2. LÝ THUYẾT TẤM KIRCHOFF
Vì bỏ qua biến dạng cắt, nên các thành phần biến dạng
trong mặt phẳng được viết ở dạng sau:
xyyxxyyx
Tz
(7.
2)
Trong đó:
yx
w
y
w
x
w
xyyx
T2
2
2
2
2
2
(7.
3)
được gọi là các thành phần độ cong.
7.2. LÝ THUYẾT TẤM KIRCHOFF
Thay các biểu thức (7.2) và (7.3
) vào quan hệ ứng suất
biến dạng
D
ta được biểu thức sau:
Dz
(7.
4)
Trong đó:
T
xyyx
2
1
00
01
01
12v
E
D
4
7.2. LÝ THUYẾT TẤM KIRCHOFF
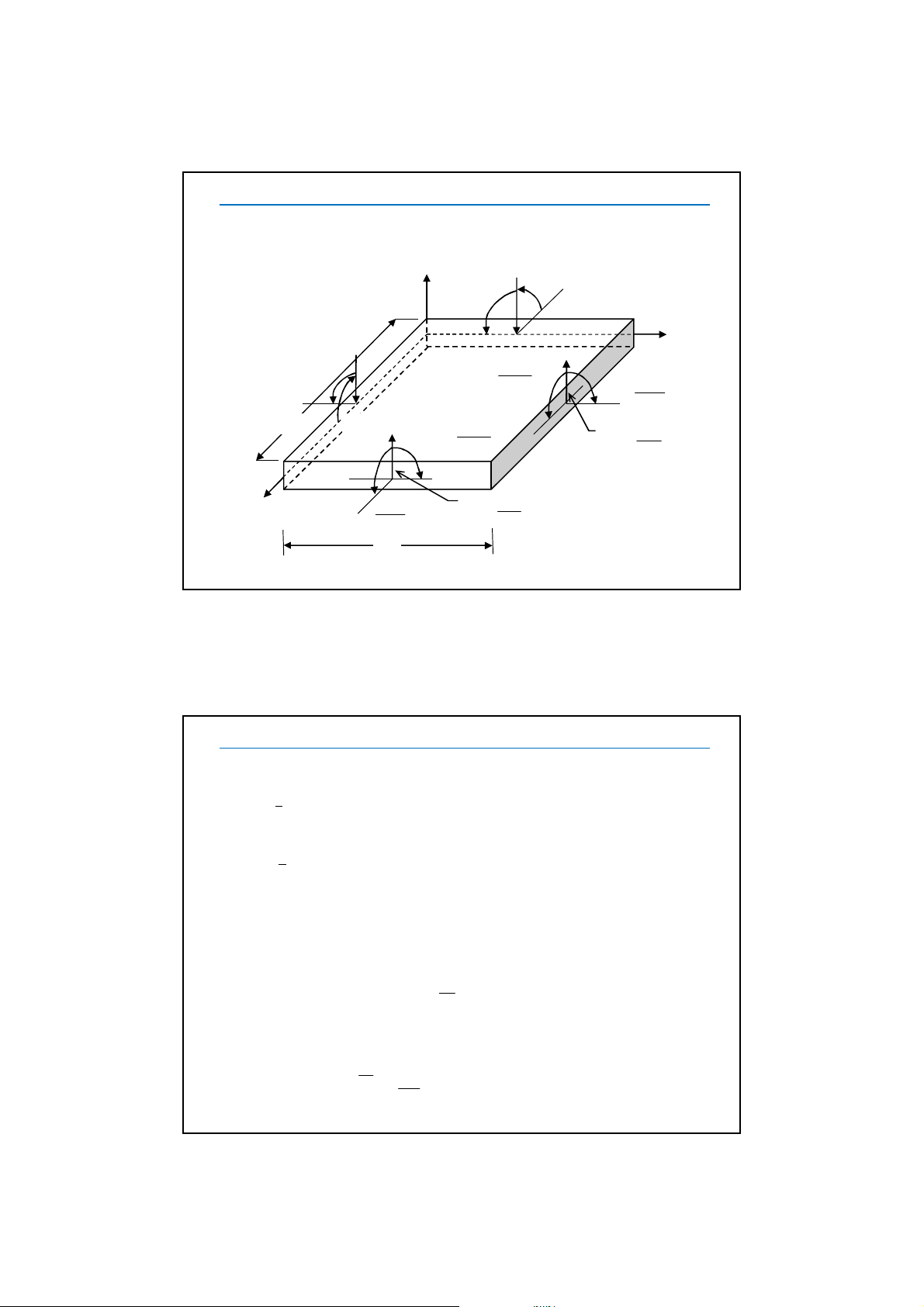
Các thành phần nội lực trên các mặt cắt ngang được mô tả
trong Hình vẽ sau.
x
y
z
Mxy Mx
Qx
Qy
Mxy
My
dy
y
M
My
y
dx
x
M
Mxy
xy
dx
x
M
Mx
x
dy
y
M
Mxy
xy
dx
x
Q
Qx
x
dy
y
Q
Qy
y
dy
dx
Hình 1. Nội lực trên phần tử tấm chịu uốn
7.2. LÝ THUYẾT TẤM KIRCHOFF
Các thành phần mômen được xác định bởi:
dzzM
h
h
2
2
(7.
5)
Trong đó:
T
xyyx MMMM
và h
là chiều dày tấm.
Thay biểu thức (7.4) vào (7.5), ta thu đư
ợc quan hệ giữa
mômen và các thành phần độ cong như sau:
M D
(7.
6)
Trong đó:
D
h
D
12
3
(7.
7)
5
7.2. LÝ THUYẾT TẤM KIRCHOFF
Các phương trình cân bằng (cân bằng mômen đ
ối với các
trục x, y và cân bằng lực đối với trục z, được suy ra từ đ
iều
kiện cân bằng tĩnh học của phần tử tấm (Hình 1).
Sau khi
đã bỏ qua các thành phần bậc cao, ta thu được các phươ
ng
trình cân bằng sau:
0
0
0
p
y
Q
x
Q
Q
y
M
x
M
Q
y
M
x
M
y
x
y
yxy
x
xy
x
(7.
8)
Trong đó, Qx và Qy là các lực cắt và p
là tải trọng phân bố
gây uốn tấm (phương tác dụng vuông góc với mặt phẳng
tấm).
7.2. LÝ THUYẾT TẤM KIRCHOFF
Khử các
thành phần lực cắt trong các phương trình của hệ
(7.8) ta được:
02 2
22
2
2
p
y
M
yx
M
x
Myxy
x
(7.
9)
Tổ hợp các biểu thức (7.3), (7.6) và (7.
9), qua một số phép
biến đổi đơn giản cuối cùng ta nhận được phươ
ng trình vi
phân cân bằng đối với tấm chịu uốn như sau:
r
D
p
y
w
yx
w
x
w
4
4
22
4
4
4
2
(7.
10)
Trong đó:
)1(12 2
3
Eh
Dr
là độ cứng chống uốn của tấm.