1
Chương 6
BÀI TOÁN PHẲNG CỦA LÝ THUYẾT ĐÀN HỒI
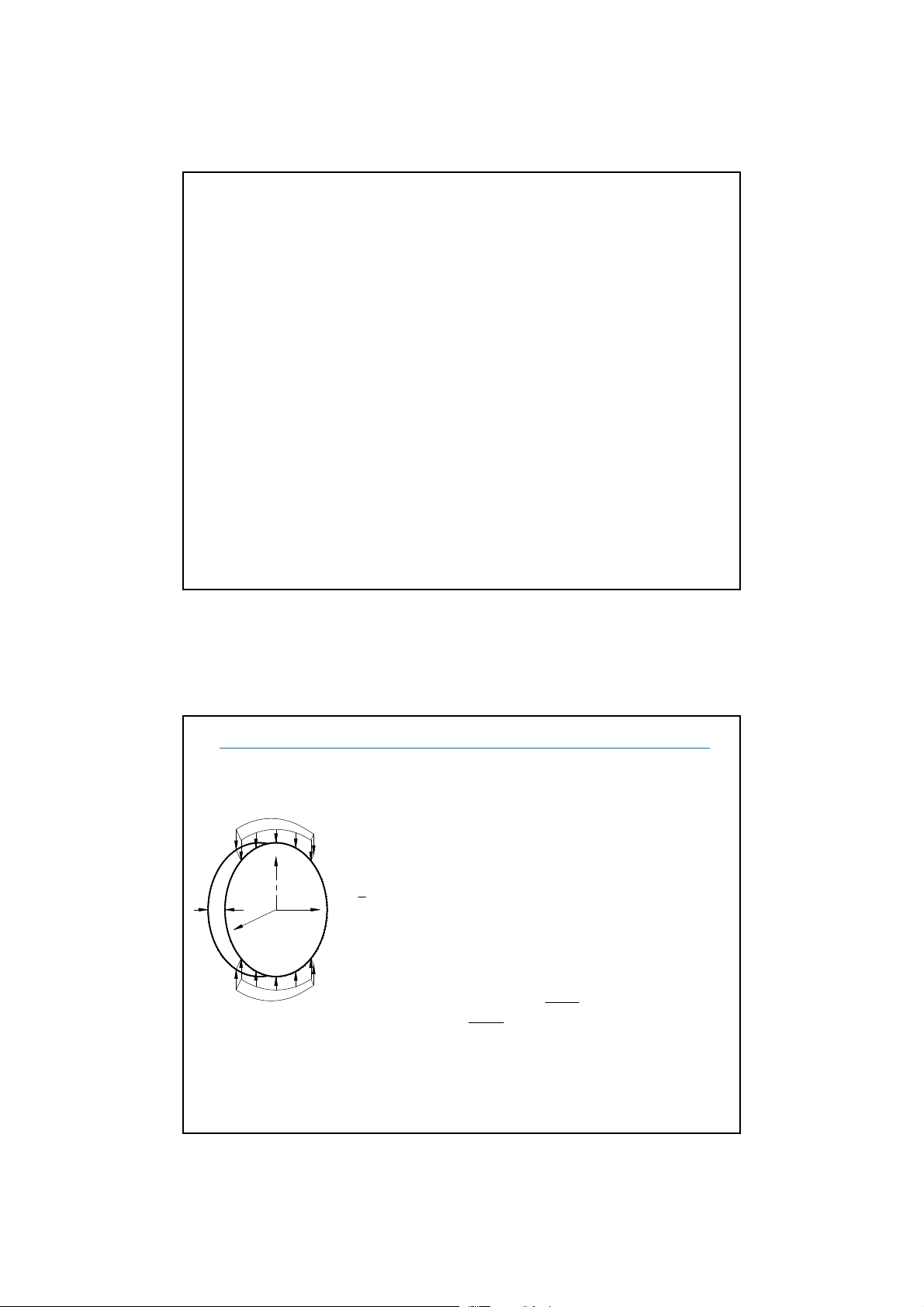
Caùc thaønh phaàn bieán daïng, chuyeån vò, öùng suaát laø haøm cuûa 2 bieán x, y.
z
y
x
t
T
x y xy
T
x y xy
T
u u v
Ñònh luaät Hooke (daïng ngöôïc):
D
2
1 2
2
1 0
1 0
1
0 0 2
C
D C C
1 2
2,
1
E
C C
Tröôøng hôïp vaät lieäu ñaúng höôùng:
6.1. BÀI TOÁN ỨNG SUẤT PHẲNG
2
z
t
Traïng thaùi bieán daïng cuûa moïi ñieåm
laø phaúng:
0
T
z x y xy
Neáu boû qua söï khaùc bieät ñoái vôùi thaønh phaàn öùng suaát vaø bieán daïng theo phöông
z thì caùc phöông trình cuûa 2 baøi toaùn naøy laø gioáng nhau. Söï khaùc bieät chæ ôû ma traän [D]
trong ñònh luaät Hooke. Cuï theå, vôùi vaät lieäu ñaúng höôùng:
1 2
1,
1 1 2 1
E
C C
6.2. BÀI TOÁN BIẾN DẠNG PHẲNG
6.3.1. Các hàm dạng
x
y
e
u =q
i1
v =q
i2
i
u =q
j3
v =q
j4
u =q
k5
v =q
k6
j
k
u(x,y)
v(x,y)
Vectô chuyeån vò nuùt phaàn töû:
6 1
T
i i j j k k
e
q u v u v u v
Vectô caùc thoâng soá:
123456
6 1
T
a a a a a a a
Tröôøng chuyeån vò cuûa phaàn töû:
1 2 3
4 5 6
,
,
e
e
u x y
a a x a y
u
a a x a y
v x y
1
2
3
4
5
6
,1 0 0 0
0 0 0 1
,
e
e
a
a
u x y
a
x y
u
a
x y
v x y
a
a

6.3. PHẦN TỬ TAM GIÁC
3
Hay goïn hôn:
,
e
u F x y a
trong ñoù:
, 0
,0 ,
P x y
F x y
P x y
vôùi:
, 1
P x y x y
Thöïc hieän ñoàng nhaát:
6 1
6 1
1 0 0 0
0 0 0 1
,
1 0 0 0
,0 0 0 1
,1 0 0 0
0 0 0 1
i i
i i
i i
j j
j j
e
j j
k k k k
k k
e
i
j
k
n
n
n
ux y
vx y
F x y
x y
u
q F x y a a
x yv
F x y x y
u
x y
v
q A a
6.3.1. Các hàm dạng
6.3. PHẦN TỬ TAM GIÁC
1 1
6 6
6 6
2 1 6 1
2 6
,
,
Vì: neân:
Hay:
e e
e e
a A q u F x y A
u N x y q
Cuï theå:
2 6
, 0 , 0 , 0
,
0 , 0 , 0 ,
i j k
i j k
N x y N x y N x y
N x y
N x y N x y N x y
vôùi caùc haøm daïng:
1
,2
1
,2
1
,2
i i jk kj
j j ki ik
k j ij ji
N x y a y x x y
A
N x y a y x x y
A
N x y a y x x y
A

&
i j k k j
ij i j
j k i i k
ij i j
k i j j i
a x y x y
x x x
a x y x y
y y y
a x y x y
i
j
k
1
1 1
det 1
2 2
1
i i
j j j k k j k i i k i j j i
k k
x y
A x y x y x y x y x y x y x y
x y
6.3.1. Các hàm dạng
6.3. PHẦN TỬ TAM GIÁC
4
Nhaän xeùt:
0
,1
neáu
neáu
i i i
i j
N x y
i j
Toång caùc haøm daïng baèng 1 hay
, ,
, 1
i
i j k
N x y
Ma traän tinh bieán daïng:
3 6 3 2 2 6
,
B N x y
3 6
0 0 0
0 0 0
jk ik ij
jk ik ij
jk jk ik ik ij ij
y y y
B x x x
x y x y x y
Deã thaáy:
e e
B q
vaø caû {
} seõ coù giaù trò khoâng ñoåi trong phaàn töû.
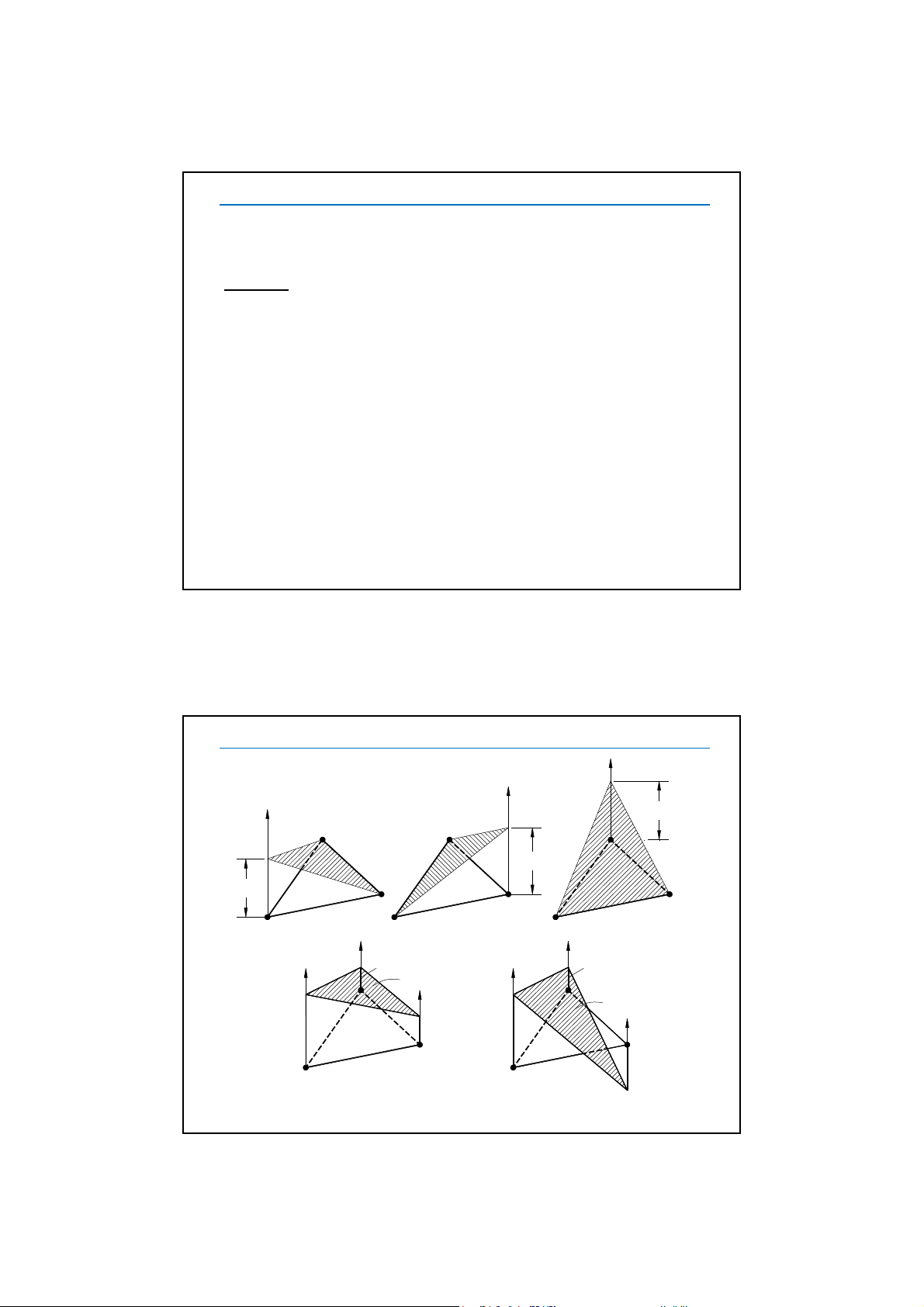
6.3.1. Các hàm dạng
6.3. PHẦN TỬ TAM GIÁC
i
j
k
1
Ni
i
j
k
Nj
1
i
j
k
Nk
1
i
j
k
u =q
i1
q =uk
5
q =uj
3
i
j
k
v =q
i2
q =vk
6
q =vj
4
u(x,y)
v(x,y)
6.3.1. Các hàm dạng
6.3. PHẦN TỬ TAM GIÁC
5
6.3.2. Ma trận độ cứng phần tử
6 3 3 3 3 6
6 6 e
T T T
e
V A
K B D B dV B D B t dA tA B D B
6.3. PHẦN TỬ TAM GIÁC
6.3.2. Ma trận độ cứng phần tử
6.3. PHẦN TỬ TAM GIÁC