Bài giảng Trí tuệ nhân tạo: Chương 4

4.1. Tri thức là gì?

• Dữ liệu và Tri thức: là những dạng khác nhau

của thông tin nên khó phân biệt rạch ròi

Tri thức

Dữ liệu

Chương 4 Chương 4 Tri thức và suy diễn

tản mạn

- ký hiệu tượng trưng - - cấu trúc phức hợp

- số - có cấu trúc - cấu trúc đơn giản

Lê Thanh Hương Khoa CNTT ĐHBK HN Khoa CNTT - ĐHBK HN

- VD: Tây y: t0 390 - - mạch 75

- VD: Đông y: - hâm hấp sốt - mạch nhanh/chậm

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Phân loại tri thức

b. Tri thức thủ tục: how?

a. Tri thức mô tả: what? a Tri thức mô tả: what?

– về tình huống (GT + KL): sự kiện – về lĩnh vực: luật nếu … thì

– Modus Ponens – Modus Ponens – Modus Tollens Tri thức cũ về tình huống --------→ Tri thức mới về t/huống

Hiểu biết về lĩnh vực

Modus Ponens Modus Tollens

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

A, A →B A →B, ¬B B ¬A • Ví dụ: Trán rộng →Thông minh Bình: trán rộng ⇒ Bình thông minh

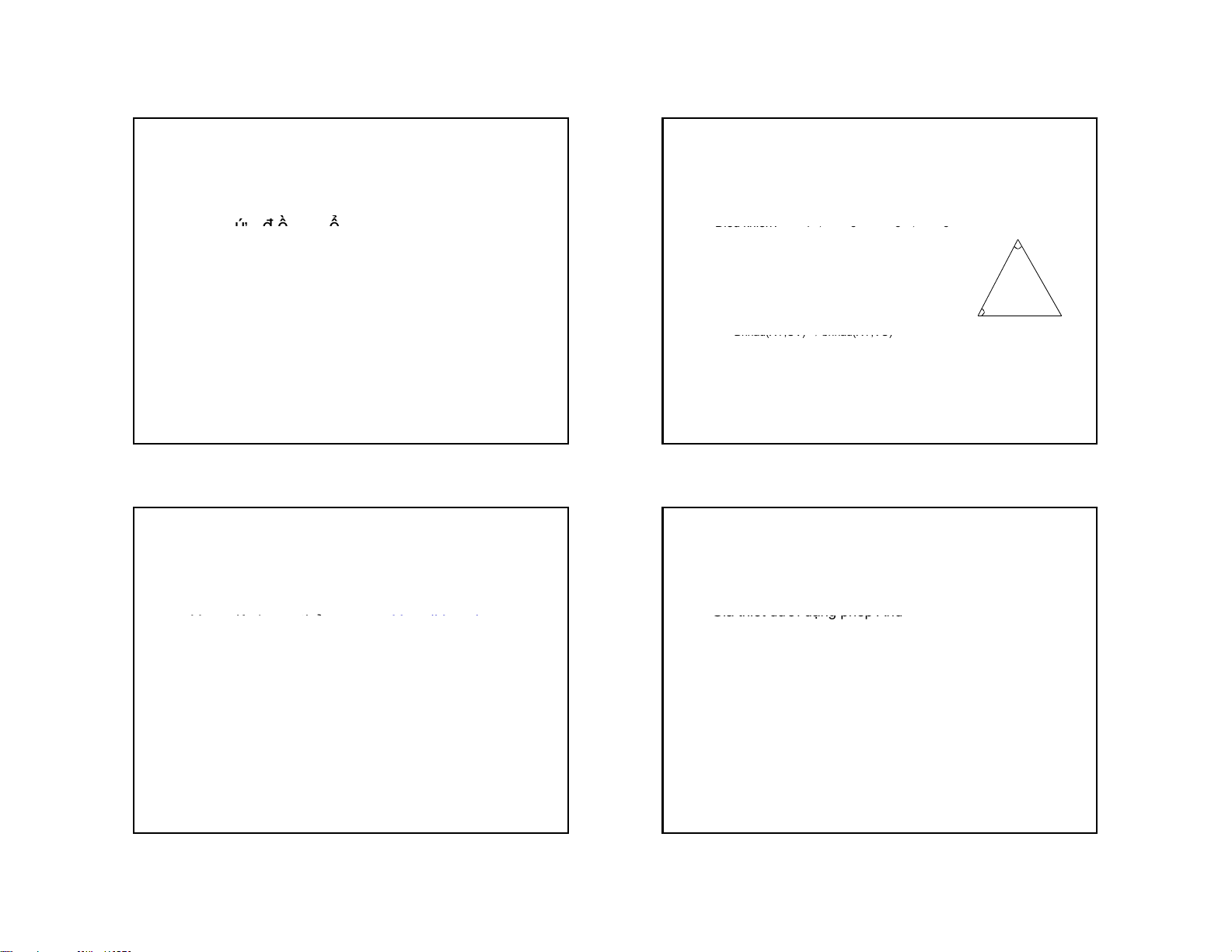
Ví dụ 1: Chứng minh bài toán hình học

Phân loại tri thức

GT, KL, hình vẽ + Định lý, tính chất

Áp dụng định lý đường trung bình vào tam giác ABC ta có

Nghĩ → SD tiến, lùi; Viết → SD tiến Nghĩ → SD tiến, lùi; Viết → SD tiến

• Mô tả? • Thủ tục? Điều khiển? • Điều khiển?

c. Tri thức điều khiển: heuristic c Tri thức điều khiển: heuristic

– Chọn hướng suy diễn: tiến, lùi, hỗn hợp – Chọn luật áp dụng: đảm bảo đủ, không

thừa, có cấu trúc, ngắn gọn

Cho X = 600, Y = 600. CM XY = XZ, XY = YZ Mô tả: • Sự kiện: Bnhau(XY,UV) Bang(X,Y) Banggoc(X,a) • Luật:

– Vẽ hình phụ

– Bnhau(XY,UV) ⇒ bnhau(UV,XY) – Bnhau(XY,UV) ⇒ bnhau(XY,VU) Bnhau(XY,UV) ⇒ bnhau(XY,VU) – Bang(Y,Z) ⇒ bnhau(XY,XZ) – Bnhau(XY,UV) ∧ bnhau(UV,ST) ⇒ bnhau(XY,ST) – ???

• Ban đầu: banggoc(X,60), banggoc(Y,60) • Đích: bnhau(XY,XZ), bnhau(XY,YZ)

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Tom và Harry

Ví dụ 2

Tri thức mô tả:

Harry

)

∧

Hare(Harry) H (H ) Tortoise(Tom)

• Harry là 1 con thỏ thỏ là 1 • Tom là 1 con rùa • Thỏ chạy nhanh hơn rùa

Giả thiết dưới dạng phép And • Giả thiết dưới dạng phép And Hare Tortoise Tom ( (

Harry

)

Tortoise

Tom (

)

Outruns

(

Harry

Tom

)

∧

→

yHare

x )(

Tortoise

y )(

Outruns

yx ,(

)

x ∀

∧

→

• Luật Hare (

Outruns O t

( (

Harry H

Tom T

) )

• Harry chạy nhanh hơn Tom?

• Kết luận

Tri thức thủ tục?

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Tri thức điều khiển?

Bản chất tri thức chuyên gia

Biểu diễn tri thức

Làm sao để chuyển tri thức từ chuyên gia con người vào máy (cid:198) kỹ sư xử lý tri thức

ử lý t i thứ

á (cid:198) kỹ

ời à

tin học

ch/gia đầu ngành lập trình viên

ε1 ∼ 0 giỏi

ksư xử lý tri thức

lĩnh vực chuyên môn giỏi ε2 ∼ 0 khá

khá

Có nhiều cách biểu diễn tri thức. Có nhiều cách biểu diễn tri thức. GT, KL → sự kiện → mệnh đề, vị từ → đỉnh R → luật → mệnh đề, vị từ, sản xuất → cung ngữ nghĩa

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

1. BDTT = logic 2. BDTT = luật sản xuất 3 3. BDTT = mạng ngữ nghĩa BDTT = mạng ngữ nghĩa 4. BDTT = frame 5. BDTT = bộ 3 Object – Attribute - Value

BDTT = logic

Ví dụ

BDTT = logic mệnh đề • BDTT = logic mệnh đề – Tri thức mô tả:

ẹp • Nếu trời đẹp thì đi chơi. p q • Nếu đi chơi và có tiền và có thời gian thì đi Hồ Tây.

– Tri thức thủ tục:

– Tri thức điều khiển: tiến, lùi

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

• Các mệnh đề p, q, r, … • Các luật suy diễn (đưa về dạng chuẩn Horn) q s t u • Nếu đi Hồ Tây và có tiền và có thời gian thì đi Nhật Tân. u s t v p1 ∧ p2 ∧ … ∧ pn ⇒ q ụ • Nếu đi Nhật Tân thì mời Lâm. • Nếu đi Nhật Tân thì mời Lâm v w • modus ponens: {A, A →B} → {A,B} • modus tollens: {A →B, ¬B} → {¬A, ¬B} • Nếu mời Lâm thì mời bạn Lâm. w x

BDTT = luật sản xuất

BDTT = mạng ngữ nghĩa

Mạng ngữ nghĩa là một đồ thị định hướng • Mạng ngữ nghĩa là một đồ thị định hướng G=(N,A), trong đó – N - tập các đối tượng, các sự kiện hay các khái

• VD: Giải bài toán lượng giác: cho biết a,b,ma.

Tìm hc

– one → một – one → người ta – one → cái

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Các luật sản xuất có dạng: • Nếu điều kiện 1 . . . . . và điều kiện m • thì kết luận 1 và … và kết luận n niệm cụ thể (đỉnh) – A - tập các mối liên hệ giữa các cặp đối tượng, sự • Trong logic mệnh đề hay vị từ, đk1…đkm, kl1…kln là những biểu thức logic, còn cặp nếu…thì thì ⇔ dấu → {(x,y) | x,y ∈ N} • Trong nguyên tắc dịch kiện hay khái niệm (cung) – A = {(x,y) | x,y ∈ N} = ∪ {(x,y) | x Ri y} ∪ {(x,y) | x Ri y} A Ri là 1 quan hệ nào đó trên tập N

BDTT = frame

• Là 1 dẫn xuất của BDTT = mạng ngữ nghĩa, là cơ sở

BDTT = bộ 3 Object – Attribute - Value

• VD: • VD:

⇔ mạng ngữ nghĩa

của phương pháp xử lý thông tin kiểu hướng đối tượng • Phương pháp BDTT = logic và mạng ngữ nghĩa mang • Phương pháp BDTT = logic và mạng ngữ nghĩa mang đặc trưng mô tả

– (bồ câu, là, chim) – (bồ câu, biết, ăn) – (bồ câu, biết, bay)

• Phương pháp BDTT = luật sản xuất : thủ tục • Phương pháp BDTT = frame kết hợp mô tả và thủ tục

• Hạn chế: chỉ thể hiện được những quan hệ “=“, khó khăn khi biểu diễn ≥, ≤, …

VD: …

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

mạng ngữ nghĩa ngữ nghĩa frame (tri thức hướng đối tượng) hướng đối tượng) đỉnh đối tượng (object) thực thể cung phân cấp (hierachy) quan hệ

Các phương pháp chứng minh

Kỹ thuật CM

Suy diễn

Chứng minh sử dụng phương pháp tìm kiếm • Chứng minh sử dụng phương pháp tìm kiếm

• Hợp giải (kỹ thuật chứng minh)

BT = GT + KL GT → KL

• Suy diễn

CM CM

GT + ¬KL → ><

R R GT + R → KL

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

– Sinh các câu mới từ các câu cũ – Chứng minh = áp dụng các luật suy diễn. Có thể h á t á tử t l ật diễ sử dụng luật suy diễn như các toán tử trong ử d phương pháp tìm kiếm chuẩn – Thường đòi hỏi chuyển các câu sang dạng chuẩn Horn

Suy diễn

Suy diễn đối với logic mệnh đề

• Dạng chuẩn Horn

Bài toán: Cho 1 CSTT R {r1, …, rn}, Bài toán: Cho 1 CSTT R={r1 r } ri là luật, ri có dạng p1∧…∧pm→q

CSTT = tập các câu ở dạng chuẩn Horn Câ H – Câu Horn =

Ngữ nghĩa:

{ 1,

• Cho biết GT={f1,…,fu} , u} • Cần CM KL={q1,…,qv} đúng • Ta nói

* a R

• các ký hiệu mệnh đề • biểu thức kết hợp các ký hiệu ⇒ ký hiệu – Ví dụ C ∧ (B ⇒ A) ∧ (C ∧ D ⇒ B) – Nếu p1 đúng và … và pm đúng – thì q đúng • Modus Ponens (cho dạng chuẩn Horn): α1, … ,αn, α1 ∧ … ∧ αn ⇒ β β β

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

• Có thể dùng cho suy diễn tiến và suy diễn lùi • Các thuật toán này có độ phức tạp tuyến tính.

Suy diễn đối với logic mệnh đề

Suy diễn

Phương pháp suy diễn: Modus Ponens:

Định nghĩa: Giả sử xét tập trung gian các sự kiện: Nếu r: p1∧…∧pm→q và p1,…,pm ∈ Tgian

thì Tgian Tgian ∪ {q} ra

r i

⇔

⊇

r i TG aa 1

r ij ... aa

* a R

A, A→B B Modus Tollens: A→B, ¬B ¬A

Nxét: quá trình SD là đơn điệu GT ⊆ TG1 ⊆ TG2 ⊆ … ⊆ TGj

• Suy diễn tiến: Xuất phát từ các mệnh đề/vị từ đã cho ban đầu, sử dụng các luật cho đến khi đưa ra kết luận mong muốn

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

• Suy diễn lùi: Xuất phát từ các kết luận mong muốn, xem những luật có khả năng suy ra chúng thêm các xem những luật có khả năng suy ra chúng, thêm các tiền đề vào d/s các KL cần CM và cứ như vậy tiếp tục đến khi d/s KL cần CM rỗng.

Suy diễn tiến

Ví dụ

Ý tưởng: • áp dụng các luật có vế trái nằm trong CSTT • bổ sung vế phải của các luật áp dụng vào CSTT

đến khi tìm thấy kết luận

6. a,B →hc 7. A,B →C 8. B,C →A 9. A,C →B 9 A C →B

VD1. Cho GT = {a,b,ma}. Tìm KL ={hc} VD1 Cho GT = {a b m } Tìm KL ={h } 1. a,b,ma →c 2. a,b,c → A 3. b,A → hc 4 a b c → B 4. a,b,c → B 5. a,b,c →C

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Thuật toán

Bài tập tại lớp

So sánh stack và queue

Vào: • Tập các mệnh đề/vị từ đã cho (ở dạng chuẩn • Tập các mệnh đề/vị từ đã cho (ở dạng chuẩn

Horn)

• Tập các luật RULE dạng p→q • Tập các mệnh đề/vị từ kết luận KL Ra: • Thông báo Thành công nếu KL có thể suy • Thông báo “Thành công” nếu KL có thể suy

ra từ GT

PP: /*Tgian là tập các mệnh đề/vị từ đúng cho

BT1. Cho GT={a }, KL={u} BT1 Cho GT={a } KL={u} 1. 2. 3. 4. a→ b b → c c → d a → u

đến thời điểm đang xét*/

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

BT2. GT={a}, KL={u} BT2 GT={a} KL={u} 1. a → b 2. d → c 3. c → u 4. a → m 5. b → n 5. b → n 6. m → p 7. p → q 8. q → u

Thuật toán

Suy diễn lùi

{1 Tgian = GT;

Thoa = Loc(Tgian,R); while Thoa <>0 and KL∉Tgian do r ← get(Thoa); /* r: left → q */ {2 R = R \ {r}; Vet = Vet ∪ {r}; Tgian = Tgian ∪ {q}; Thoa = Loc(Tgian,R)

6. a,B→ hc B h 6 7. b,A → hc 8. c,S → hc 9. a,b,c → S 1’. ha,c → B

VD: 1. A,C → B B 1 A C 2. a,b,ma →c 3. a,b,c → A 4. a,b,c → B 5. a,b,c → C GT={a,b,ma}; KL={hc}

}2 if KL ⊆ Tgian then exit(“Thành công”) else exit(“Không thành công”)

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Suy diễn lùi

ự ệ

ập

Ý tưởng: suy diễn lùi từ kết luận KL • • •

Đầu: • Goal = tập các sự kiện cần CM=KL • Goal = {f| f cần CM cho đến thời điểm

•

hiện tại}

Tránh lặp vô tận: – –

kiểm tra xem KL đã được biết chưa, nếu không chứng minh bằng quay lui sử dụng các luật dẫn đến q chứng minh bằng quay lui sử dụng các luật dẫn đến q

• Vet ={(f,j)| để CM f thì dùng luật j: leftj→f} • Cờ Back = true khi quay lui

false không quay lui

•

Tránh lặp lại công việc: kiểm tra xem KL mới – –

lưu trữ các đích đã được chứng minh trước khi chứng minh kiểm tra xem đích cần chứng minh đã có trong goal stack chưa?

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

đã ở trong tập đã được chứng minh chưa đã làm nhưng thất bại chưa

f ← lấy từ GOAL

s

đ

goal = 0?

OK

Suy diễn lùi

f ∈ GT s

Tìm rj: leftj → f

1. Quá trình SD lùi tương tự quá trình

g ự q

đ

not OK

Tìm được

Vet = Vet ∪{(f,j)} Goal = Goal ∪ leftj\GT

đ

s

Q tìm cây/đồ thị lời giải trong đồ thị V/H 2. Để tăng hiệu quả của thủ tục SDL, có

s

f ∈KL?

đối với f thử dùng rj

(g,k) ← Vet: Tìm (g,k) ∈ VET rk: leftk → g; f ∈ leftk

thể đưa vào 2 tập: – Tập Đúng chứa các sự kiện đã được khẳng định là đúng (đã xác định) khẳ (đã á đị h)

đị h là đú

– Tập Sai chứa các sự kiện đã được khẳng

Tìm luật (g,l), l>k

định là sai (không thể xác định)

s

đ

Tìm được

f = g

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

Goal = Goal\leftk Goal = Goal ∪ leftl\GT Vet = Vet ∪{(g,l)} 31

So sánh SD tiến và SD lùi

Bài tập tại lớp

BT1. Cho GT {a,b,ma}, BT1. Cho GT={a,b,ma},

• SD tiến hướng dữ liệu, tự động, không định hướng. Ví dụ, nhận dạng đối tượng, xác định hướng. Ví dụ, nhận dạng đối tượng, xác định hành trình

• Có thể làm rất nhiều việc không liên quan

đến KL

• SD lùi hướng KL, thích hợp cho các bài toán giải quyết vấn đề Ví dụ tìm chìa khoá lập giải quyết vấn đề. Ví dụ, tìm chìa khoá, lập kế hoạch thi TOEFL

• Độ phức tạo của SD lùi thường nhỏ hơn rất

KL={hc} 1. a,b,ma → c 2. a,b,C → s 3. a,s → ha 4. b,s → hb 5 c s 5. c,s → hc h 6. a,B → hc 7. a,b,c → B

nhiều so với kích thước của CSTT.

Lê Thanh Hương – Khoa CNTT - ĐHBKHN

BT2. GT={a}, KL={u} BT2 GT={a} KL={u} 1. a → b 2. d → c 3. c → u 4. a → m 5. b → n 6. m → p 7. p → q 8. q → u

Suy diễn đối với logic vị từ

GT AI=IB, BJ=JC, CK=KD, DL=LA

KL IJKL là hình bình hành

VD1: Xét bài toán chứng minh hình học VD1: Xét bài toán chứng minh hình học

Suy diễn đối với logic vị từ trd(U,XY) (cid:198) trd(U,YX) 1. trd(U,XY), trd(V,XZ) (cid:198) ss(UV,YZ) trd(U XY) trd(V XZ) (cid:198) ss(UV YZ) 2. 2 3. ss(XY,UV), ss(UV,ST)(cid:198) ss(XY,ST) 4. ss(XY,VU), ss(XV,YU) (cid:198) hbh(XYUV) 5. ss(XY,UV) (cid:198) ss(XY,VU) 6. ss(XY,UV) (cid:198) ss(UV,XY)

D D

GT: trd(I,AB), trd(J,BC), trd(K,CD), trd(L,DA) KL: hbh(IJKL)

1. 2. 3. 4. 5. 6. 7. 8 8. 9. •

Fred là con chó giống Collie. Sam là chủ của nó. Hôm nay là thứ bảy. Thứ bảy trời lạnh. Fred là con chó được huấn luyện. Chó spaniel và (chó collie được huấn luyện) là chó tốt. Nếu một con chó tốt và có ông chủ thì nó sẽ đi cùng ông chủ. Nếu thứ bảy và ấm thì Sam ở công viên Nếu thứ bảy và ấm thì Sam ở công viên. Nếu thứ bảy và không ấm thì Sam ở viện bảo tàng. Hỏi fred ở đâu? ∃X loc(fred,X)

1. 2. 3. 4. 5. 6. 7. 8. 9.

collie(Fred). owner(Sam, Fred). day(sat). cold(sat). trained(Fred). spaniel(X) ∨ (collie(X) ∧ trained(X)) (cid:198) gooddog(X). gooddog(X) ∧ owner(Y,X) ∧ loc(Y,Z)(cid:198) loc(X,Z). day(sat) ∧ ¬cold(sat) (cid:198) loc(Sam, park). day(sat) ∧ cold(sat) (cid:198) loc(Sam,museum).

Lê Thanh Hương – Khoa CNTT - ĐHBKHN