TRƯỜNG ĐẠI HỌC BÁCH KHOA Tp.HCM
CHƯƠNG 3
CHƯƠNG
3
DẪN NHIỆT QUA THANH
–
CÁNH
DẪN
NHIỆT
QUA
THANH
–
CÁNH
1. Dẫn nhiệt qua thanh có tiếtdiện không đổi
2
Dẫn
nhiệt
qua
có
tiết
diện
không
đổi
2
.
Dẫn
nhiệt
qua
có
tiết
diện
không
đổi
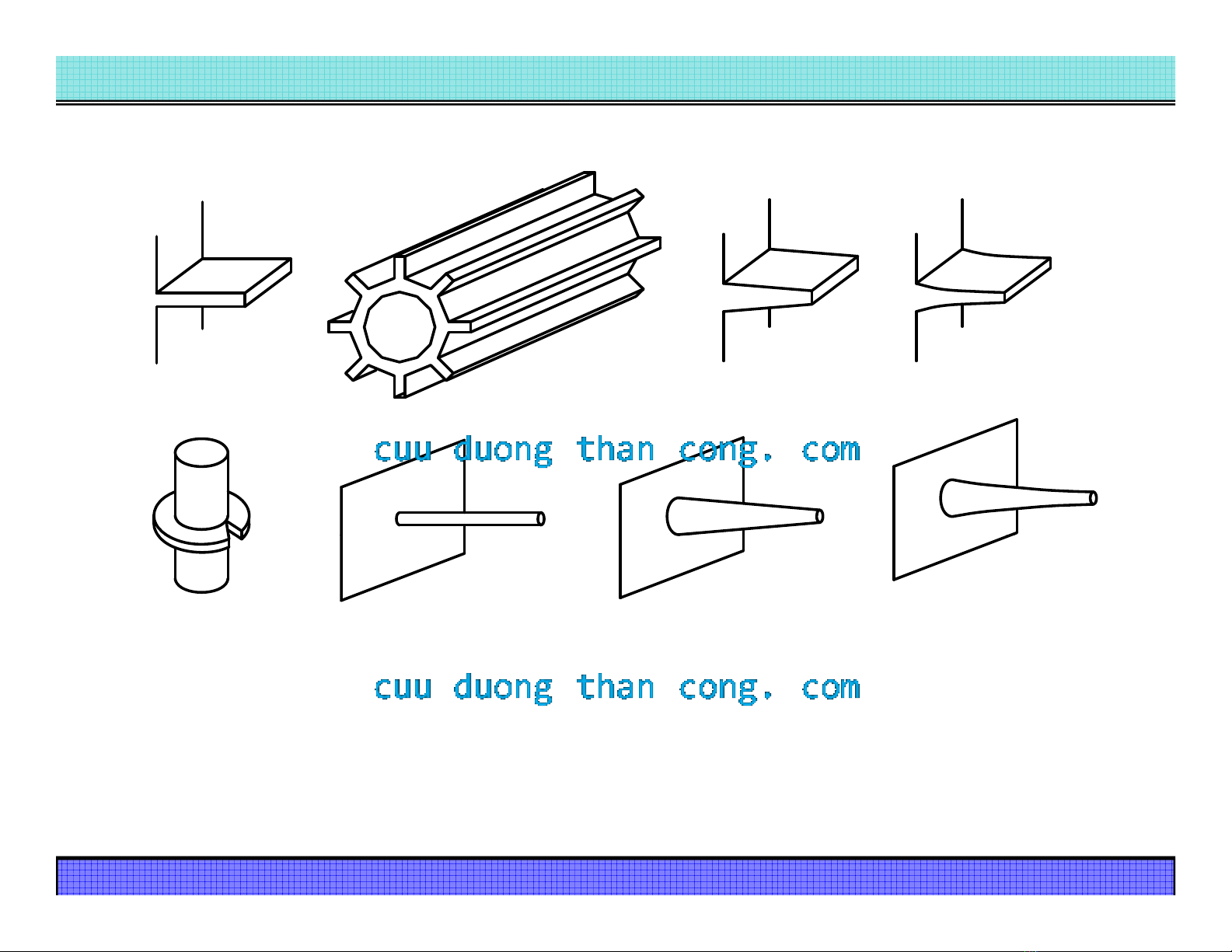
3. Dẫn nhiệt qua cánh có tiếtdiện thay đổi
4. Dẫn nhiệt qua cánh tròn
5
Ph
há
íh
hiệ
ấ
1
Cán bộ giảng dạy: Ths. Phan Thành Nhân
5
.
Ph
ương
phá
pt
í
n
h
hiệ
usu
ấ
t
CuuDuongThanCong.com https://fb.com/tailieudientucntt
TRƯỜNG ĐẠI HỌC BÁCH KHOA Tp.HCM
Khái quát về dẫn nhiệt qua bề mặt cánh:
Doøng nhieät ñoái löu truyeàn töø beà maët coù nhieät ñoä ts ñeán nhieät ñoä
moâi tröôøng t
theo ñònh luaät Newton:
ttFQ s
2
Cán bộ giảng dạy: Ths. Phan Thành Nhân
CuuDuongThanCong.com https://fb.com/tailieudientucntt
TRƯỜNG ĐẠI HỌC BÁCH KHOA Tp.HCM
Một sốbieân dạng caùnh
3
Cán bộ giảng dạy: Ths. Phan Thành Nhân
CuuDuongThanCong.com https://fb.com/tailieudientucntt
TRƯỜNG ĐẠI HỌC BÁCH KHOA Tp.HCM
1. Quaù trình daãn nhieät qua thanh coù tieát dieän ngang khoâng ñoåi:
– Thanh coù tieát dieän khoâng ñoåi, vôùi dieän tích maët caét ngang f,
chu vi u.
– Heä soá toûa nhieät khoâng ñoåi treân toaøn boä beà maët thanh.
– Heä soá daãn nhieät
–
Gia
û
ñònh
ra
è
ng
nhieät
ñoä
thay
ño
å
i
theo
phöông
doc
truc
thanh
Gia
ñònh
rang
nhieät
ñoä
thay
ñoi
theo
phöông
do
ï
c
tru
ï
c
thanh
,
– Ñoä cheânh nhieät ñoä cuûa thanh vôùi nhieät ñoä moâi tröôøng :
f
tt
4
Cán bộ giảng dạy: Ths. Phan Thành Nhân
CuuDuongThanCong.com https://fb.com/tailieudientucntt
TRƯỜNG ĐẠI HỌC BÁCH KHOA Tp.HCM
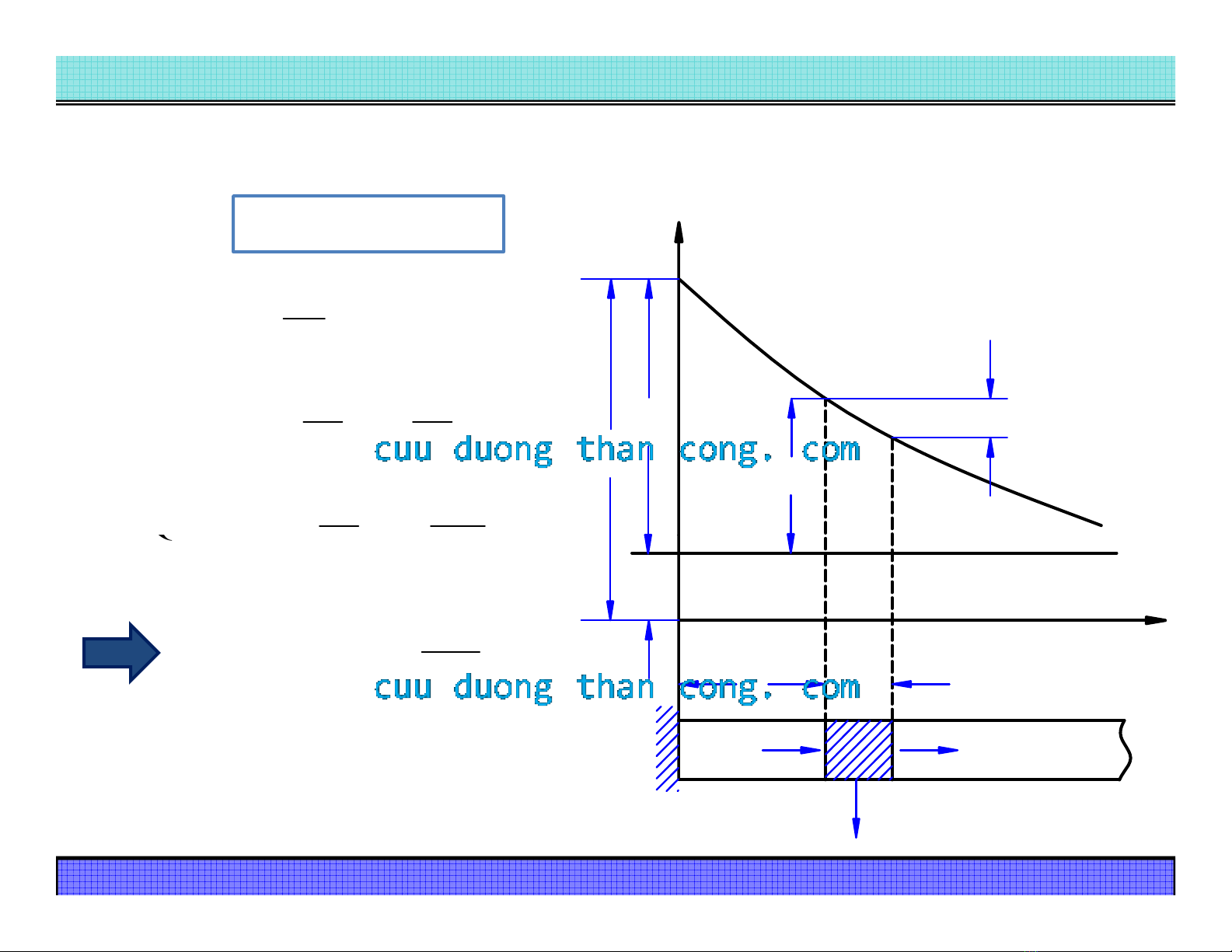
Xeùt quaù trình truyeàn nhieät treân moät ñôn vò daøi dx:
dQQQ dxxx
t
d
d
f
dx
d
Qx
f
d
d
d
Q
d
t
1
dx
d
f
d
f
Q
f
d
x
dxdx
Q
2
2
dx
x
dxx
t
f
x
dxdx
Q
2
dx
x
dx
d
f
Q
Q
2
dx
Q
x
Q
x+dx
x
dx
dx
f
Q
Q
2
dxxx
Theo ñònh luaät Newton
5
Cán bộ giảng dạy: Ths. Phan Thành Nhân
dQ
udxdQ 
CuuDuongThanCong.com https://fb.com/tailieudientucntt