BỘ CÔNG THƯƠNG
TRƯỜNG ĐẠI HỌC CÔNG NGHIỆP HÀ NỘI
---------------------------------------
MÔN HỌC
TỐI ƯU TRONG GIA CÔNG CẮT GỌT
Hà Nội -2025
Bài 1. (bài 4.4, trang 106)
a) Trình bày các bước thuật giải PSO trong xây dựng bài toán tối ưu hóa?
b) Dùng phương pháp PSO giải để xác định chế độ cắt tối ưu.
*Ví Dụ 4.4: Ứng dụng thuật toán PSO để tối ưu hóa quá trình gia công phay
cạo tốc bằng dao phay ngón lưỡi nhỏ với hàm mục tiêu độ nhám bề mặt nhỏ
nhất với điều kiện biên và miền giới hạn của bài toán.
Hàm mục tiêu tối ưu hóa chế độ cắt là:
Y=Ra=0,1441.v−0,3023 . f 0,3824 . ar
0,0572 → nhỏ nhất
- Tham số lực quán tính:
Bài toán xác định bộ thông số chế độ cắt tối ưu v,f,a, để độ nhám bề mặt nhỏ
nhất. Tuy vậy, giá trị chế độ cắt không phải là giá trị bất kỳ mà không có yêu
cầu ràng buộc nào phải phụ thuộc vào từng điều kiện hệ thống công nghệ trong
quá trình gia công. Với hệ thống công nghệ gia công lại có giá trị giới hạn cho
các điều kiện biên và miền giới hạn khác nhau.
v . Fc≤ Pdc .η.60 .1000=G1
Lực cắt theo phương Y ảnh hưởng lớn nhất tới quá trình cắt gọt:
v . Fc=2163. v0,4721 . f 0,2678 . ar
0,5260 ≤ Pdc .η .60 .1000=G1
Miền giới hạn của phạm vi điều chỉnh tốc độ cắt;
G2=vmin ≤ v ≤ vmax=G3
Miền giới hạn của phạm vi điều chỉnh lượng chạy dao;
G4=fmin ≤ f =1000. v
π . D . N . f z≤ f max=G5
Miền giới hạn của phạm vi điều chỉnh chiều sâu cắt;
G6=armin ≤ ar≤ armax =G7
Giới hạn về rung động trrong quá trình gia công để đảm bảo độ ổn định của rung
động;
Axy=
√
Ax
2+Ay
2≤
[
A0
]
=G8
Với hàm
Độ võng của dụng cụ cắt đảm bảo nhỏ hơn độ võng cho phép[Y].Theo sức bền
vật liệu đối với trực congxo ta có thể xác định được độ võng tài phần đầu của
dụng cụ cắt [2d]:
ymax=c . F
E[L1
3
D1
4−L2
3−L1
3
D2
4]
m
≤[δ]=G10
đối với dụng cụ cắt thí nghiệm D1=D2=20gmm; L1 - chiều dài phần lưỡi cắt
(theo hãng dụng cụ cắt Sandvik chế tạo L1=15gmm); L2 - chiều lưỡi cắt (theo
hãng dụng cụ cắt (thực nghiệm gã trị L2=25gmm); E - môđun đàn hồi của vật
liệu dụng cụ cắt (MPa); C,m - hệ số phụ thuộc vào đặc tính hình học dao phay
ngón sử dụng thực nghiệm (đối với dao phay ngón kiểu có 4 lưỡi cắt, 3 lưỡi cắt
và 2 lưỡi cắt thì tương ứng hệ số C là 9,05; 8,30 và 7,93; hệ số m tương ứng là
0,950, 0,965 và 0,974) [24]. Vậy khi đó ta có dụng cụ cắt sử dụng thực nghiệm
có 4 lưỡi cắt vị quá trình thực nghiệm gia công tinh. Khi đó có hệ số C=9,05; hệ
số m=0,95 thay vào phương trình có:
Ymax=9,05. F
E[152
204+253−153
204]
0,95
=0,993. F
E≤[δ]
Với F là lực cắt khi phay:
Fxy=
√
Fx
2+Fy
2
Trong đó hàm tổng hợp lực cắt với thành phần X,Y (Fxy) có phương trình như
sau:
Fxy=2735,2. v−0,5345 . f 0,2608 . ar
0,5527
Giải các bài toán tối ưu trong công nghệ gia công cơ khí là lớp các bài toán thực
nghiệm ứng với từng điều kiện công nghệ cụ thể. Vì giải quyết vấn đề nên các
hàm mục tiêu và giới hạn biên phải tiếp cận đến các hàm thực nghiệm. Cách tiếp
cận như vậy mới đáp ứng được yêu cầu công nghệ ngày càng chính xác và khắt
khe hiện tại và trong thời gian tới. Trên thực tế, với sự phát triển nhanh của khoa
học công nghệ, vấn đề các hệ thống mới ra đời đòi hỏi chi phí máy móc, trang
thiết bị dụng cụ ngày càng lớn. Vấn đề tối ưu trong công nghệ để đem lại chất
lượng và hiệu quả kinh tế là vấn đề quan trọng và cần thiết.
Giải:
Thuật toán tối ưu hóa bầy đàn (PSO) tính toán chế độ cắt tối ưu để đạt được độ
nhám bề mặt nhỏ nhất.
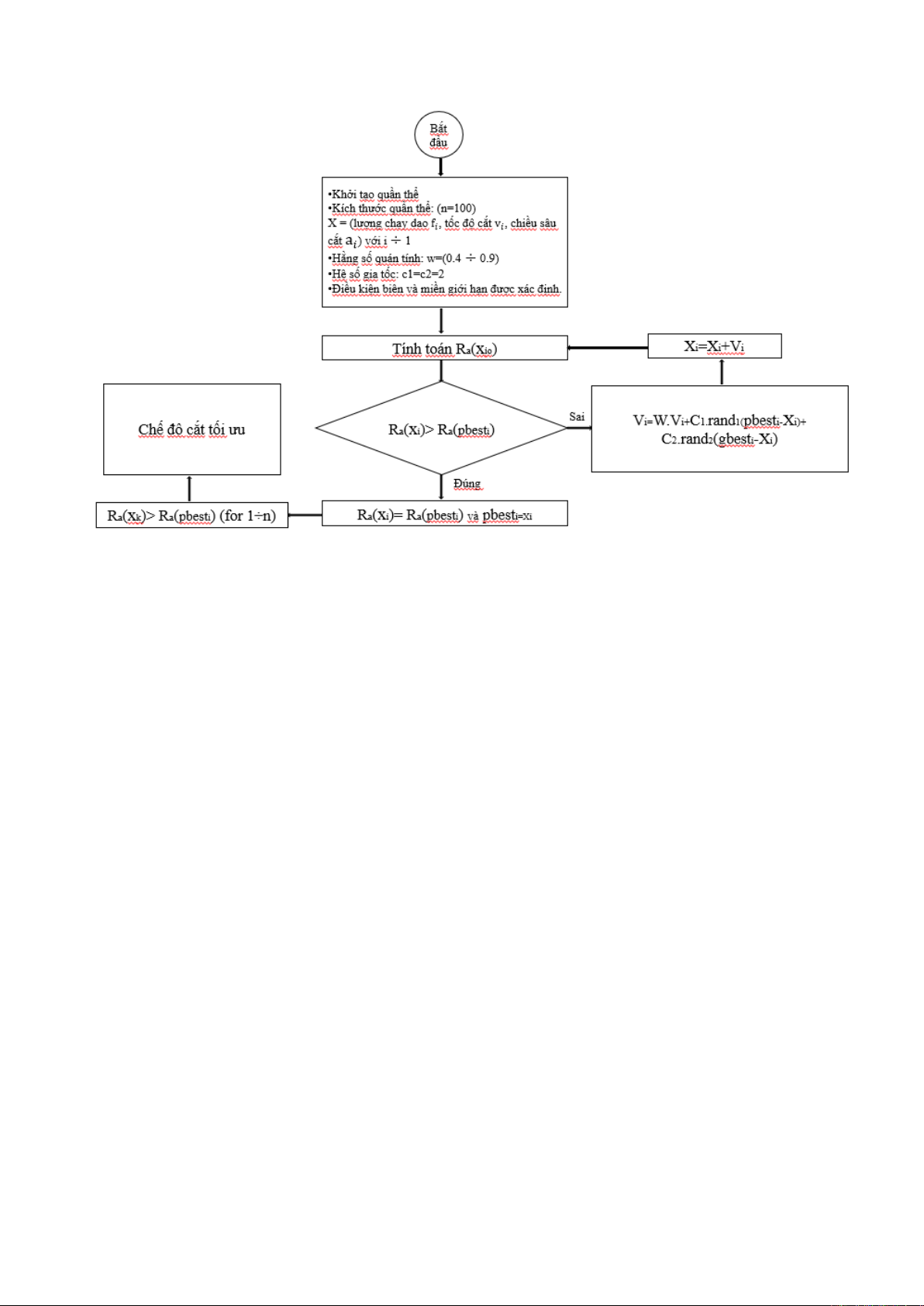
Bước 1: Khởi tạo quần thể với việc khởi tạo vector vị trí xi và vector vận tốc vi
(i=1,...,n) (cho mỗi cá thể Pi trong quần thể P(n)). Vector vị trí xi(Vi,fi,ari) với
mỗi giá trị Vi,fi,ari trong quần thể Pi. Khai báo điều kiện biên và miền giới hạn
của bài toán.
Bước 2: Khởi tạo các thông tin ban đầu về vị trí tốt nhất của các cá thể và cả
quần thể.
pbesti=xi
(khởi tạo vị trí tốt nhất của cá thể thứ i bằng vị trí hiện tại);
gbesti=min ⁡(Ra(xi))
i = 1,...n (khởi tạo vị trí tốt nhất trong tất cả các bằng vị trí
không nào hòa bằng được giá trị yêu cầu trong tất cả cá thể).
Bước 3: Bước lặp vị trí kiến lập xac định thửc (sau môt số lần lặp cho thửc hòa
sau môt số lần lặp mà không thu đuc két qua tôt hon) for i=1:n (với môt cá thể).
vi
k+1=w . vi
k+c1. rand1.
(
pbesti−xi
k
)
+c2.rand2.
(
gbesti−xi
k
)
(cập nhật lại chuyển động của thế
hệ tiếp theo chuyền động tốt nhất hiện tại của chính cá thế và theo chuyền đông
của cá thể tốt nhất trong quần thể).
xi
k+1=xi
k+vi
k+1
(cập nhật lại vị trí hiện tại theo hướng chuyển động mới nhất).
If
Ra
(
xi
)
<Ra
(
pbesti
)
then
pbesti=xi
(Cập nhật lại vị trí tốt nhất của một cá thể bằng
việc so sánh với vị trí hiện tại). Nếu If
Ra
(
xi
)
<Ra
(
gbesti
)
then
gbesti=xi
(cập nhật lại
vị trí tốt nhất của quần thể bằng việc so sánh với cá thể tốt nhất hiện tại). Với
một giá trị
xi
, so sánh với điều kiện biến thiên thỏa mãn thì mới thực hiện bước
tiếp theo.
2163. v0,4721 . f 0,2678 . ar
0,5260 ≤ Pdc . η .60.1000=G1
G2=vmin ≤ v ≤ vmax=G3
G4=fmin ≤ f =1000. v
π . D . N . f z≤ f max=G5
G6=armin ≤ ar≤ armax =G7
A ≤
[
A0
]
=G8trong đó A=Axy=1,653. v−0,0766 . f 0,0911 . ar
0,3542
0,993. F
E≤[δ]
Trong đó :
F=Fxy=2735,2. v−0,5345 . f 0,2608 . ar
0,5527
-Kiểm tra điều kiện kết thúc bước lặp, nếu thỏa mãn chuyển sang bước 4, còn
không tiếp tục bước 3.
Bước 4: Kết thúc,trả về giá trị tốt nhất
gbesti
- Kết quả đánh giá kết quả bài toán