
Dao ®éng & Sãng c¬
(Ch−¬ng 8-9)
Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn
ViÖn VËt lý kü thuËt
Tr−êng §H B¸ch khoa Hμnéi

• Lùc kÐo vÒ vÞ trÝ c©n b»ng
• Qu¸n tÝnh
• VÞ trÝ c©n b»ng
Tù ®äc: Dao ®éng, Sãng
☛§iÒu kiÖn
hÖ dao ®éng:
9Tæng hîp hai dao ®éng Cïng tÇn sè ωcïng
ph−¬ng x
Cïng tÇn sè, Ph−¬ng vu«ng gãc
)(sin)cos(
aa
xy
2
a
y
a
x
12
2
12
21
2
2
2
2
1
2
ϕ−ϕ=ϕ−ϕ−+
9Tæng hîp hai dao ®éng vu«ng gãc (Xem BT
1.1) Cïng tÇn sè ω:
x=a1cos(ωt+ϕ1)
y=a2cos(ωt+ϕ2)
)(sin)cos(
aa
xy
2
a
y
a
x
12
2
12
21
2
2
2
2
1
2
ϕ−ϕ=ϕ−ϕ−+
Sù h×nh thμnh sãng c¬ trong m«i tr−êng
chÊt
✻C¸c ®Æc tr−ng cña sãng
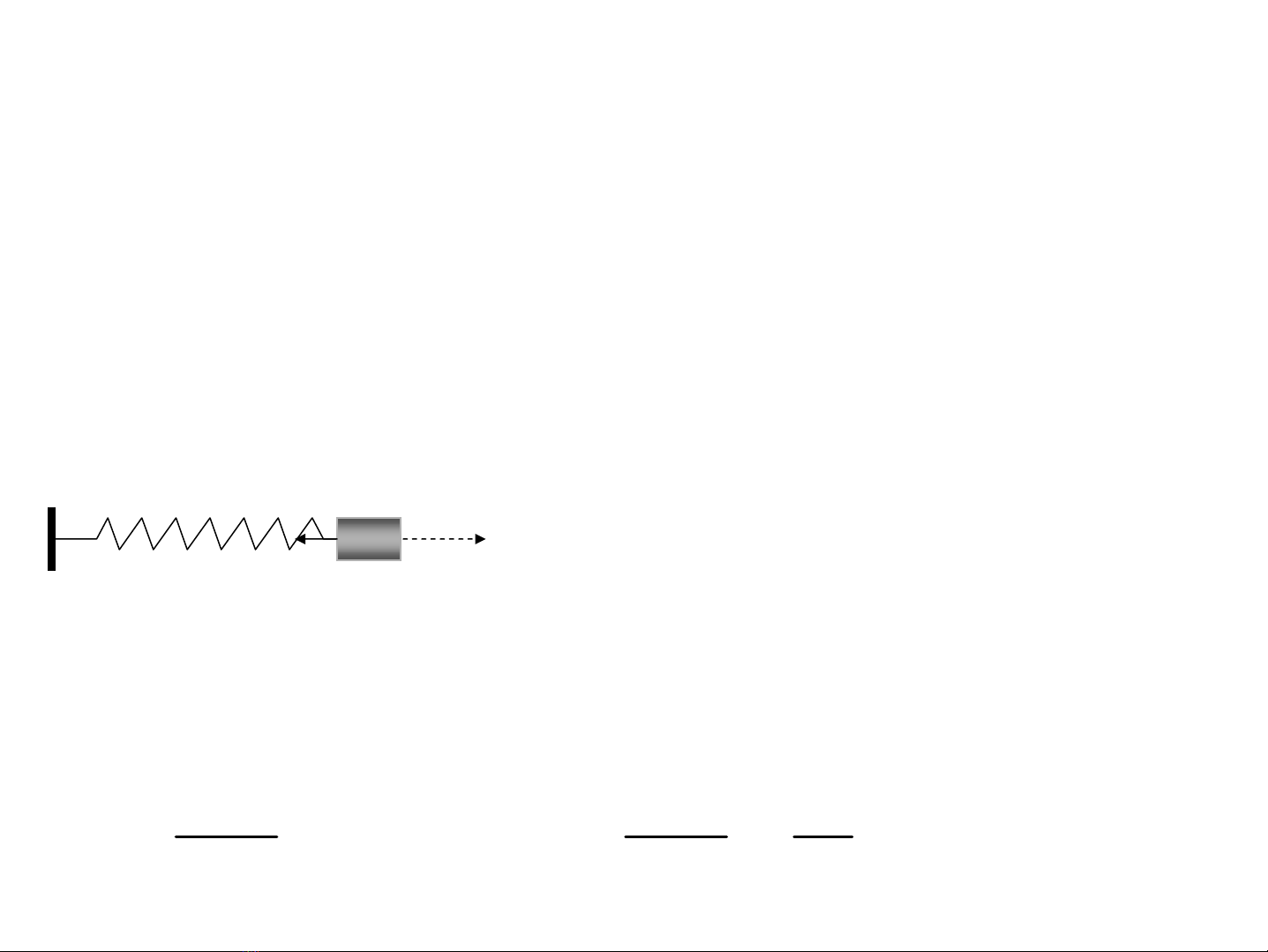
• Lùc kÐo vÒ vÞ trÝ c©n b»ng
• Qu¸n tÝnh
1. Dao ®éng c¬ ®iÒu hoμ
x
Dao ®éng: chuyÓn ®éng ®−îc lÆp l¹i nhiÒu lÇn
theo thêi gian
kxF −=
✌Kh«ng cã ma s¸t ->
dao ®éng c¬ ®iÒu hoμ
1.2. Ph−¬ng tr×nh dao ®éng c¬ ®iÒu hoμ
kx
dt
xd
m2
2
−= 0x
m
k
dt
xd
2
2
=+
• VÞ trÝ c©n b»ng
☛§iÒu kiÖn
hÖ dao ®éng:

2
0
m
kω= 0x
dt
xd 2
0
2
2
=ω+ 0
0>
ω
)tcos(Ax 0ϕ
+
ω
=
✍Dao ®éng ®iÒu hoμlμdao ®éng cã ®é dêi lμ
hμmsèSIN hoÆc COS theo thêi gian
1.3. Kh¶o s¸t dao ®éng ®iÒu hoμ
• Biªn ®é dao ®éng: A=|x|max
m
k
0=ω
• TÇn sè gãc riªng
• Pha cña dao ®éng:(ω0t+ϕ),t=0->ϕpha ban ®Çu.
• VËn tèc con l¾c: )tsin(A
dt
dx
v00 ϕ+ωω−==











![Bài tập Vật lý sóng: Tổng hợp bài tập 6 [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250805/oursky04/135x160/401768817575.jpg)














