V K THU T V K THU T
Ẽ Ỹ Ẽ Ỹ
Ậ Ậ
NG III NG III
: V HÌNH H C : V HÌNH H C
ƯƠCH ƯƠ CH
Ọ Ọ
Ẽ Ẽ
S d ng b ng v S d ng b ng v
ử ụ ử ụ
ả ả
ẽ ẽ
ướ
ằ
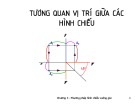
Tr Tr
t th t êke d c th
c T, ta v đ ọ
c các đ ẽ ượ ườ c T đ v các đ ể ẽ
ướ
ng song song n m ngang. ng song song th ng ườ
ẳ
ượ ượ đ ng.ứ
V HÌNH H C
Ọ
Ẽ
V đ V đ
ng phân giác ng phân giác
ẽ ườ ẽ ườ
A
V HÌNH H C
Ọ
Ẽ
I. CHIA Đ U ĐO N TH NG I. CHIA Đ U ĐO N TH NG
Ạ Ạ
Ẳ Ẳ
Ề Ề
Chia thành 02, 04, 08… đo n b ng nhau:
ạ
ằ
A B
V HÌNH H C
Ọ
Ẽ
I. CHIA Đ U ĐO N TH NG I. CHIA Đ U ĐO N TH NG
Ạ Ạ
Ẳ Ẳ
Ề Ề
ằ
ấ
Thành nhi u đo n b ng nhau b t kỳ ạ Ví d chia 03 ph n
ề ầ
ụ
a
a
a
A B
V HÌNH H C
Ọ
Ẽ
II. CHIA Đ U Đ II. CHIA Đ U Đ
NG TRÒN NG TRÒN
Ề Ề
ƯỜ ƯỜ
Thành 02, 04, 08… ph nầ
O
V HÌNH H C
Ọ
Ẽ
II. CHIA Đ U Đ II. CHIA Đ U Đ
NG TRÒN NG TRÒN
Ề Ề
ƯỜ ƯỜ
Chia thành 03, 06…ph n, đ
ng tròn bán kính
ầ
ườ
R.
O
V HÌNH H C
Ọ
Ẽ
III. Đ D C III. Đ D C
Ộ Ố Ộ Ố
Ký hi u đ d c: ho c Ký hi u đ d c: ho c ặ ộ ố ặ ộ ố
ệ ệ
1:6
1
6
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
Các nguyên t c c b n c n nh : ớ ng tròn
Đ ng th ng a ti p xúc đ
ắ ơ ả ế
ầ ườ
ườ
ẳ
a
O
a ^
R (OT) = T
T
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
ắ ơ ả ợ
ầ ữ
ườ
Các nguyên t c c b n c n nh : ớ ng tròn bán Đ ng t p h p tâm c a nh ng đ ườ ng th ng a. ẳ
ậ kính R, ti p xúc v i đ ế
ủ ớ ườ
t
O
a
R
O
R
O T
ng th ng
ẳ
ườ
R
T
t là đ t // a t và a cách nhau R
T
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
Các nguyên t c c b n c n nh :
ơ ả
ớ
ắ
ầ
ng tròn (O1,R1) và ( O2,R2)
ti p xúc
ườ
ế
Hai đ ngoài
O1
1
R
T ˛ O1O2 O1O2 = R1 + R2
T
2
R
O2
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
ắ
ơ ả
ớ
ầ
ng tròn
ườ
(O2, R2) ti p ế
ậ xúc ngoài v i đ
ủ ng tròn
ườ ữ (O1, R1) cho tr
Các nguyên t c c b n c n nh : Đ ng t p h p tâm c a nh ng đ ợ ớ ườ
c.ướ
O2 R
2
T
R 1
O1
R
1
R
1
T
2
T
R
O2
ườ
R
(O1, R1+R2)
2
O2
Đ ng tròn Tâm: O1 Bán kính = R1 + R2
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
ắ ơ ả
ầ
ng tròn (O1,R1) và ( O2,R2)
Hai đ
ti p xúc trong
Các nguyên t c c b n c n nh : ớ ế
ườ
T
R
R
2
1
O2
O1
T ˛ O1O2 O1O2 = R1 – R2
R1 – R2
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
ầ
ườ
(O2, R2) ti p ế
ậ xúc trong v i đ
ơ ả ủ ng tròn
ữ ườ (O1, R1) cho tr
Các nguyên t c c b n c n nh : ớ ắ Đ ng t p h p tâm c a nh ng đ ng tròn ợ ớ ườ
c.ướ
T
T O2
R
2
O2
R
– R2 R1
1 – R
2
ườ
O1 R1
2
1 – R
R
O2
Đ ng tròn Tâm: O1 Bán kính = R1 - R2
T
(O1, R1-R2)
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
bán kính r ti p xúc v i đ ế
ớ ườ
ng th ng và ẳ
V cung tròn đ
ng tròn.
Ví d 1:ụ ẽ ườ
r
ị
ầ
Oo r
T1
C n xác đ nh: 1 – Bán kính. 2 – Tâm. 3 – Các ti p đi m. ế
ể
O
r
a T2
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
ng tròn cho
ng th ng qua đi m A và ti p xúc đ ể
ế
ườ
c (ph
ẳ ng pháp hình h c)
Ví d 2:ụ V đ ẽ ườ tr ướ
ươ
ọ T
O1
A
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
Ví d 2:ụ
ng tròn cho
ế
ườ
c (ph
ẳ ng pháp th c d ng)
V đ ẽ ườ tr ướ
ng th ng qua đi m A và ti p xúc đ ể ự
ươ
ụ
T
O1
A
V HÌNH H C
Ọ
Ẽ
IV. V N I TI P IV. V N I TI P
Ẽ Ố Ế Ẽ Ố Ế
ng tròn cho tr
c, có
ế
ườ
ướ
Ví d 3:ụ V đ ẽ ườ R1 > R2 (ph
ng th ng ti p xúc v i 02 đ ng pháp th c d ng)
ẳ ươ
ớ ự
ụ
T1
O1 T2
O2