Giới thiệu Khoảng tin cậy cho trung bình Khoảng tin cậy cho tỷ lệ Xác định kích thước mẫu Xác định độ tin cậy
KHOẢNG TIN CẬY
TĂNG LÂM TƯỜNG VINH
Khoa Toán - Tin Học
Đại Học Khoa Học Tự Nhiên Tp.HCM
Tp. Hồ Chí Minh, 09/2021
TĂNG LÂM TƯỜNG VINH XÁC SUẤT THỐNG KÊ
KHOẢNG TIN CẬY 1
Giới thiệu Khoảng tin cậy cho trung bình Khoảng tin cậy cho tỷ lệ Xác định kích thước mẫu Xác định độ tin cậy
Nội dung
1Giới thiệu
2Khoảng tin cậy cho trung bình
3Khoảng tin cậy cho tỷ lệ
4Xác định kích thước mẫu
5Xác định độ tin cậy
TĂNG LÂM TƯỜNG VINH XÁC SUẤT THỐNG KÊ
KHOẢNG TIN CẬY 2
Giới thiệu Khoảng tin cậy cho trung bình Khoảng tin cậy cho tỷ lệ Xác định kích thước mẫu Xác định độ tin cậy
Giới thiệu
•Giả sử ta cần khảo sát 1 đặc tính Xtrên 1 tổng thể xác định.
•Biến ngẫu nhiên Xcó phân phối F(x;θ), tham số θchưa biết.
•Chọn 1 mẫu ngẫu nhiên cỡ n:X= (X1, . . . , Xn).
Định nghĩa
Một ước lượng khoảng (interval estimator) của 1 tham số θlà 1
cặp các thống kê L(X1, . . . , Xn)và U(X1, . . . , Xn)của 1 mẫu
ngẫu nhiên thỏa L(X)≤U(X)và L(X)≤θ≤U(X). Nếu 1
mẫu thực nghiệm x= (x1, . . . , xn)được quan trắc, [l(x), u(x]gọi
là 1 khoảng ước lượng (interval estimate) cho θ.
TĂNG LÂM TƯỜNG VINH XÁC SUẤT THỐNG KÊ
KHOẢNG TIN CẬY 3
Giới thiệu Khoảng tin cậy cho trung bình Khoảng tin cậy cho tỷ lệ Xác định kích thước mẫu Xác định độ tin cậy
Khoảng tin cậy
Định nghĩa
Xét biến ngẫu nhiên X= (X1, . . . , Xn)có hàm mật độ đồng thời
phụ thuộc vào tham số θ∈Rvà L(X)và U(X)là 2 thống kê sao
cho L(X)≤U(X). Khi đó khoảng ngẫu nhiên [L(X), U(X)] gọi
là khoảng tin cậy cho tham số θvới độ tin cậy 100(1 −α)% nếu
PL(X)≤θ≤U(X)= 1 −α
Với mẫu thực nghiệm x= (x1, . . . , xn), ta có khoảng tin cậy cụ
thể cho tham số θlà
l(x)≤θ≤u(x)
TĂNG LÂM TƯỜNG VINH XÁC SUẤT THỐNG KÊ
KHOẢNG TIN CẬY 4
Giới thiệu Khoảng tin cậy cho trung bình Khoảng tin cậy cho tỷ lệ Xác định kích thước mẫu Xác định độ tin cậy
Khoảng tin cậy
Ý nghĩa
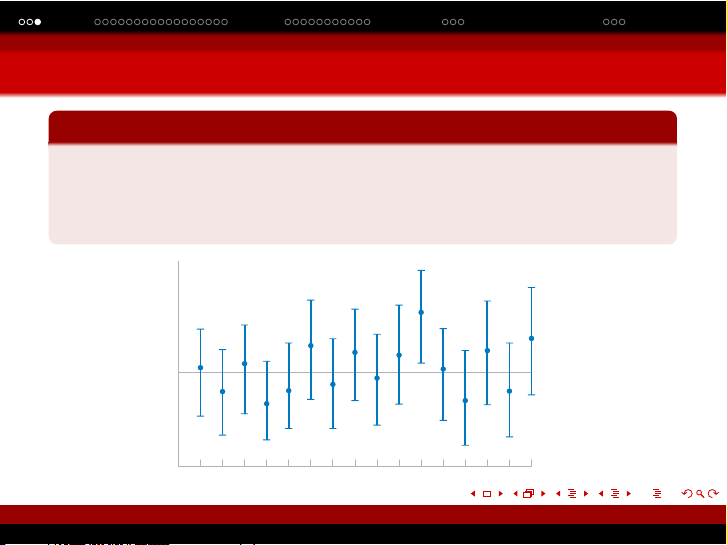
Với 100% lần lấy mẫu cỡ nthì
•có 100(1 −α)% lần giá trị tham số θ∈[l, u]
•có 100α%lần giá trị tham số θ6∈ [l, u]
Interval number
µ
12345678910111213141516
Repeated
uction of a con-
.
TĂNG LÂM TƯỜNG VINH XÁC SUẤT THỐNG KÊ
KHOẢNG TIN CẬY 5