®¹i häc B¸ch khoa Hµ néi Khoa C«ng nghÖ th«ng tin
Xö lý ¶nh NguyÔn ThÞ Hoµng Lan
Ch−¬ng 7
Ph©n vïng ¶nh
1. Kh¸i qu¸t chung
• Mét vµi kh¸i niÖm
- Mét vïng ¶nh R (Region) : lµ tËp hîp cña c¸c ®iÓm ¶nh cã cïng chung c¸c thuéc tÝnh
thuéc vÒ mét ®èi t−îng trong ¶nh.
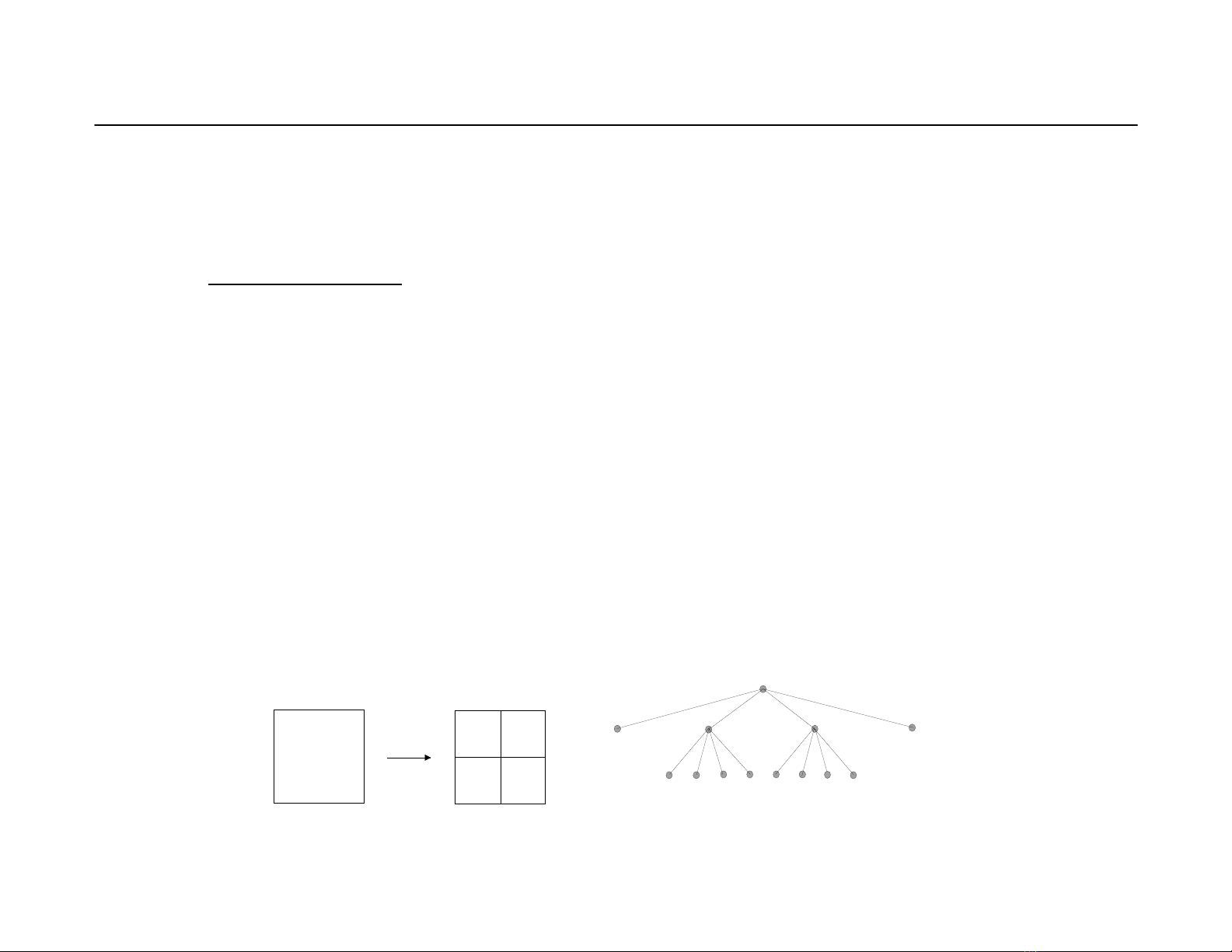
- Ph©n vïng ¶nh (segmentation): lµ qu¸ tr×nh ph©n ho¹ch tËp hîp c¸c ®iÓm ¶nh X thµnh c¸c
tËp con cña c¸c vïng ¶nh Ri tho¶ m·n c¸c ®iÒu kiÖn sau :
∅≠∀ Ri
i,
∅
=
∩
≠∀ Rj
i
jiji R
,, et
i
Ri
X
∪
=
, Ri bao gåm c¸c pixel cã thuéc tÝnh chung.
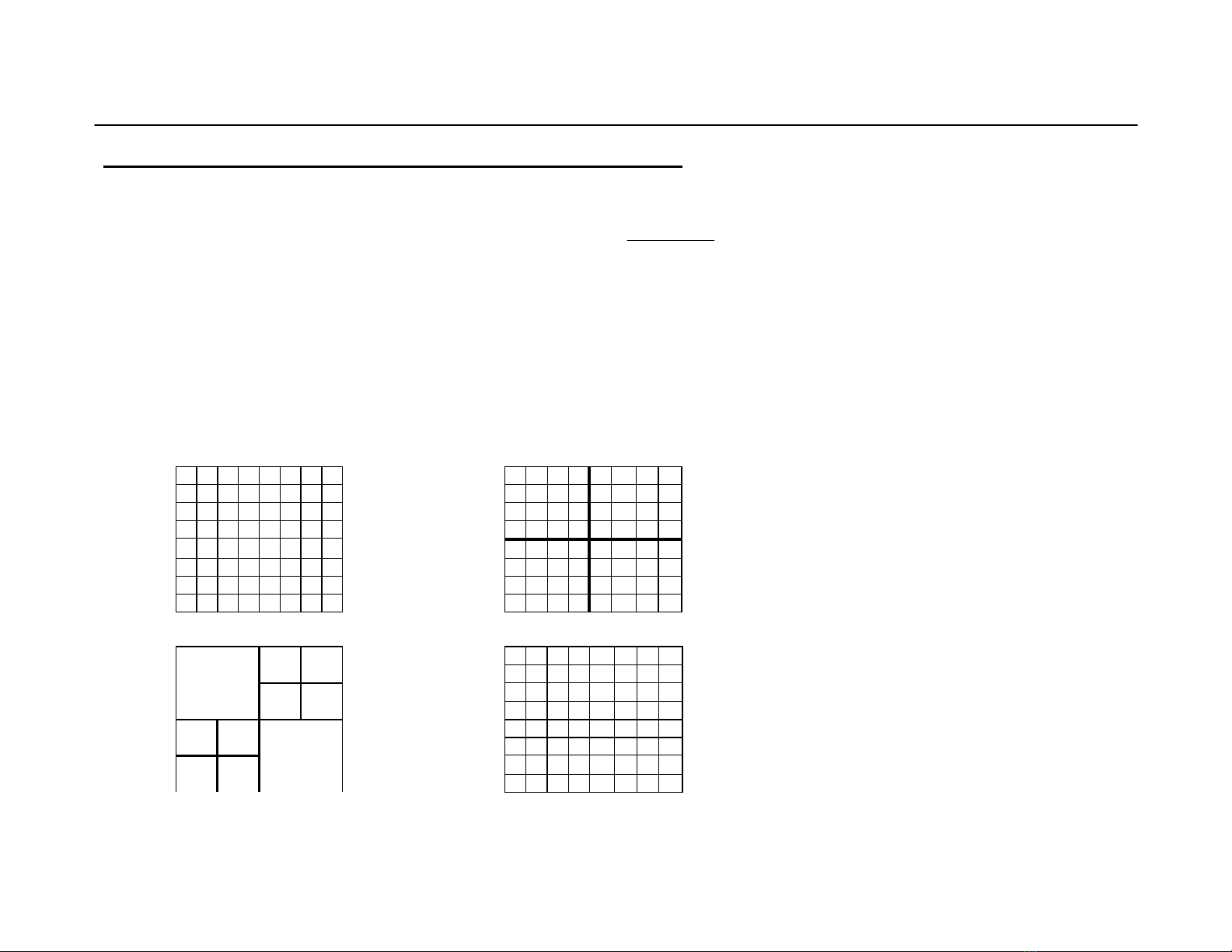
• C¸c h−íng tiÕp cËn cña ph©n vïng ¶nh
- Ph©n vïng dùa trªn ®é ®ång ®Òu, ®é t−¬ng tù vÒ møc x¸m vµ vÒ c¸c thuéc tÝnh cña c¸c
pixel trong mçi vïng.
- Ph©n vïng dùa trªn t¸ch biªn dùa trªn sù biÕn thiªn cña hµm ®é s¸ng hay møc x¸m
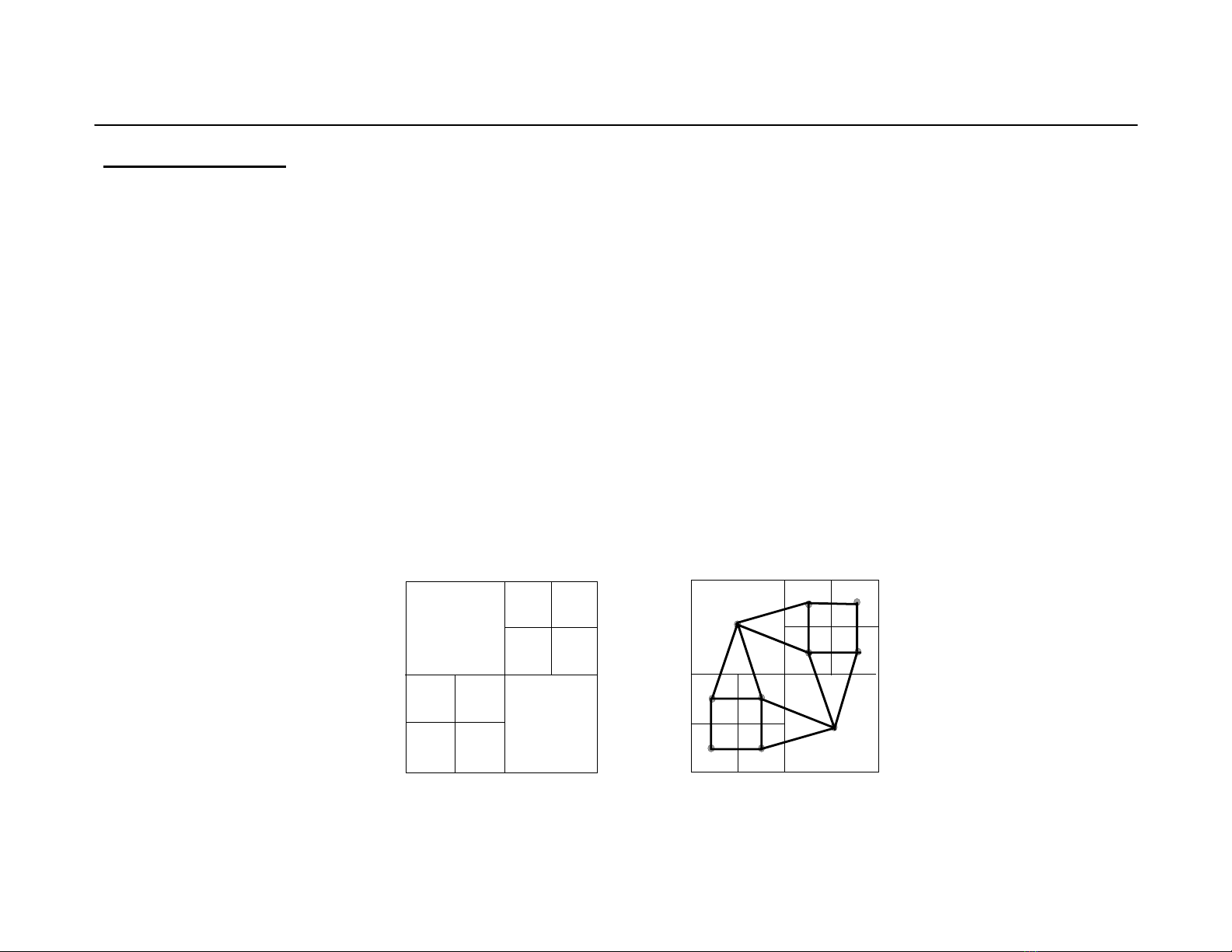
• C¸c c«ng ®o¹n chñ yÕu cña ph©n vïng ¶nh : - TiÒn xö lý
- Qu¸ tr×nh ph©n vïng (thuËt to¸n)
- ®¸nh nh·n ph©n t¸ch c¸c vïng vµ hiÖu chØnh
®¹i häc B¸ch khoa Hµ néi Khoa C«ng nghÖ th«ng tin
Xö lý ¶nh NguyÔn ThÞ Hoµng Lan
• Mét sè ph−¬ng ph¸p ph©n vïng
- Ph©n vïng dùa trªn sù ph©n líp c¸c ®iÓm ¶nh trong kh«ng gian thuéc tÝnh mét chiÒu
hoÆc kh«ng gian thuéc tÝnh nhiÒu chiÒu,
- Ph©n vïng theo ph−¬ng ph¸p cÊu tróc,
- Ph©n vïng dùa trªn biÓu diÔn vµ xö lý ®a ph©n gi¶i,
- Ph©n vïng dùa trªn ph©n tÝch kÕt cÊu (texture).
2. C¸c thuéc tÝnh cña ®iÓm ¶nh vµ cña vïng ¶nh
• Thuéc tÝnh biªn ®é
• ®é ®ång ®Òu vÒ møc x¸m, ®é t−¬ng ph¶n
• Thuéc tÝnh tÇn sè
• Thuéc tÝnh thèng kª, tham sè th«ng kª
• Thuéc tÝnh h×nh häc, tham sè h×nh häc
• Thuéc tÝnh cÊu tróc (texture) ...
3. Ph−¬ng ph¸p ph©n líp
• Sù ph©n líp
- Kh¸i niÖm vÒ líp c¸c c¸ thÓ (c¸c phÇn tö) : tËp hîp c¸c phÇn tö cã chung thuéc tÝnh
- Sù ph©n líp : ph©n lo¹i c¸c phÇn tö vÒ c¸c líp theo c¸c tiªu chuÈn vÒ thuéc tÝnh
- Mét vïng ¶nh Rk ®−îc x¸c ®Þnh bëi c¸c pixel thuéc vÒ mét líp Ck
®¹i häc B¸ch khoa Hµ néi Khoa C«ng nghÖ th«ng tin
Xö lý ¶nh NguyÔn ThÞ Hoµng Lan
• Ph−¬ng ph¸p ph©n líp c¸c ®iÓm ¶nh trong kh«ng gian thuéc tÝnh ®a chiÒu
Tiªu chuÈn ph©n líp : kho¶ng c¸ch gi÷a c¸c vect¬ thuéc tÝnh
• Ph©n líp c¸c ®iÓm ¶nh trong kh«ng gian thuéc tÝnh 1 chiÒu : thuéc tÝnh biªn ®é
- Tiªu chuÈn ph©n líp dùa trªn c¸c ng−ìng gi¸ trÞ møc x¸m gi÷a c¸c vïng
- ThuËt to¸n ISODATA (Iterative Self Organization DATa Analysis)
B−íc ®Çu (t = 0) + ®o¸n nhËn sè líp M
+ Lùa chän c¸c gi¸ trÞ ng−ìng ban ®Çu gi÷a c¸c líp Tj(0)
B−íc lÆp (t = 1, 2 ...) : + Thùc hiÖn ph©n líp theo c¸c ng−ìng Tj(t-1)
+ TÝnh gi¸ trÞ trung b×nh trong mçi líp mk(t)
+ TÝnh c¸c gi¸ trÞ ng−ìng míi Tj(t) theo c¸c gi¸ trÞ mk(t)
+ KiÓm tra ®iÒu kiÖn lÆp
B−íc cuèi: + Ph©n líp c¸c ®iÓm ¶nh theo c¸c gi¸ trÞ ng−ìng ®¹t ®−îc khi thuËt to¸n héi tô,
+ ®¸nh nh·n thuéc tÝnh, ph©n t¸ch c¸c vïng vµ hiÖu chØnh sè líp nÕu cÇn,
+ Ph©n t¸ch c¸c vïng
4. Ph−¬ng ph¸p cÊu tróc
• ThuËt to¸n lan to¶ vïng
• ThuËt to¸n ph©n vïng dùa trªn sù ph©n chia vµ kÕt hîp c¸c miÒn kÒ
Nguyªn t¾c chia ¶nh dùa trªn cÊu tróc c©y tø ph©n
Ri
Ri1 Ri2
Ri3 Ri4
Rx
R11 R12 R13 R14
R121 R122 R123 R124 R131 R132 R133 R134
®¹i häc B¸ch khoa Hµ néi Khoa C«ng nghÖ th«ng tin
Xö lý ¶nh NguyÔn ThÞ Hoµng Lan
ThuËt to¸n ph©n chia miÒn kÒ d−¹ trªn cÊu tróc c©y tø ph©n
• ChØ tiªu ph©n chia
Sè ®o ®é ®ång ®Òu thuéc tÝnh cu¶ miÒn R:
()
∑
∈
−
=
Rs
RmsA
Rcard
R)()(
)(
1
)( 2
σ
vµ Hµm vÞ tõ : Pred(R)
NÕu
σ
(R) >
θ
th× Pred(R) = 0, nghÜa lµ ®é kh«ng ®ång ®Òu
• Nguyªn t¾c thuËt to¸n
- Ph©n chia liªn tiÕp c¸c miÒn kÒ theo cÊu tróc c©y tø ph©n cho ®Õn khi ®¹t ®−îc tÊt c¶ c¸c miÒn ®ång ®Òu
- X©y dùng c©y tø ph©n cña ¶nh
- TÝnh sai sè b×nh ph−¬ng cña ¶nh sau qu¸ tr×nh chia
VÝ dô
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2
1 1 1 1 1 2 2 2 1 1 1 1 1 2 2 2
1 1 1 1 2 2 2 2 1 1 1 1 2 2 2 2
1 1 1 1 1 2 2 2 1 1 1 1 1 2 2 2
1 1 1 1 1 2 2 2 1 1 1 1 1 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
0000 00 3.3
0000 00 3.3
0000.8.200
0000.2.200
0000.9.11.1
0000.9.11.1
0000.1.11,1
0000.1.11.1
®¹i häc B¸ch khoa Hµ néi Khoa C«ng nghÖ th«ng tin
Xö lý ¶nh NguyÔn ThÞ Hoµng Lan
ThuËt to¸n kÕt hîp
• ®å thÞ c¸c miÒn kÒ G(V, E)
V : TËp c¸c nót t−¬ng øng víi c¸c miÒn kÒ. E : TËp c¸c cung, c¸c liªn kÕt
Hai miÒn kÒ Ri vµ Rj ®−îc nèi bëi mét cung trªn ®ã mang gi¸ trÞ vÒ ®é ®o sù kh«ng ®ång ®Òu thuéc tÝnh gi÷a 2 miÒn E(Ri, Rj).
• ChØ tiªu kÕt hîp
Hai miÒn kÒ Ri vµ Rj sÏ ®−îc kÕt hîp thµnh mét miÒn R : RR
Rji ∪
=
nÕu gi¸ trÞ ®é ®o vÒ sù kh«ng ®ång ®Òu thuéc tÝnh
gi÷a 2 miÒn lµ nhá nhÊt. Qu¸ tr×nh kÕt hîp ®−îc dùa trªn sù kiÓm tra ®iÒu kiÖn vÒ sai sè b×nh ph−¬ng nh− sau :
()
∑∑ −
=∈
=
N
kRk
s
k
R
msA
NE
1
)()(
)( 2
• Néi dung thuËt to¸n kÕt hîp
- B−íc ®Çu : X©y dùng ®å thÞ c¸c miÒn kÒ cña ¶nh sau qu¸ tr×nh ph©n chia : G(V, E), vµ chän ng−ìng
- B−íc lÆp : KÕt hîp c¸c miÒn kÒ Ri et Rj t−¬ng øng víi c¸c cung cã gi¸ trÞ nhá nhÊt.
CËp nhËt ®å thÞ c¸c miÒn kÒ G(V, E) vµ tÝnh sai sè E(N) sau mçi lÇn kÕt hîp
KiÓm tra ®iÒu kiÖn lÆp dùa trªn E(N)
- B−íc cuèi : KÕt qu¶ ph©n vïng dùa trªn ®å thÞ c¸c miÒn kÒ sau qu¸ tr×nh lÆp, t¸ch c¸c vïng vµ hiÖu chØnh (nÕu c©n)
m= 1,0
m= 1,0
m= 1,0
m= 1,0
m= 2,0 m= 2,0
m= 1,9
m= 1,8
m= 1,3
m= 2,0 00
0
0
0
22
4,2
2,6 1,8
1,8
0,9
0,9
0,9
2,6
1,43
a) b)