Chương 2:
TÍN HIỆU VÀ HỆ THỐNG RỜI RẠC
TRONG MIỀN THỜI GIAN
Giảng viên: Ths. Đào ThịThu Thủy
Chương 2: TÍN HIỆU & HỆ THỐNG RỜI RẠC
2.1 Tín hiệu rời rạc
2.2 Hệ thống rời rạc
2.3 Hệ thống tuyến tính bất biến LTI
2.4 Phương trình sai phân mô tả hệ thống rời rạc
2.5 Cấu trúc hệ thống rời rạc
2.6 Tương quan giữa các tín hiệu
2.1 TÍN HIỆU RỜI RẠC
2.1.1 Biểu diễn tín hiệu rời rạc
Tín hiệurờirạcđượcbiểudiễnbằng mộtdãycácgiátrị
vớiphầntửthứnđượckýhiệux(n).
Với Ts:chu kỳ lấy mẫu
n : số nguyên
Tín hiệu rời rạc
xs(nTs) ≡x(n)
Lấy mẫu
Tín hiệu liên tục
xa(t) Ts=1
t = nTs
9Tín hiệurờirạccó thểbiểudiễnbằng mộttrongcác
dạng: hàm số,dạng bảng, dãy số&đồ thị.
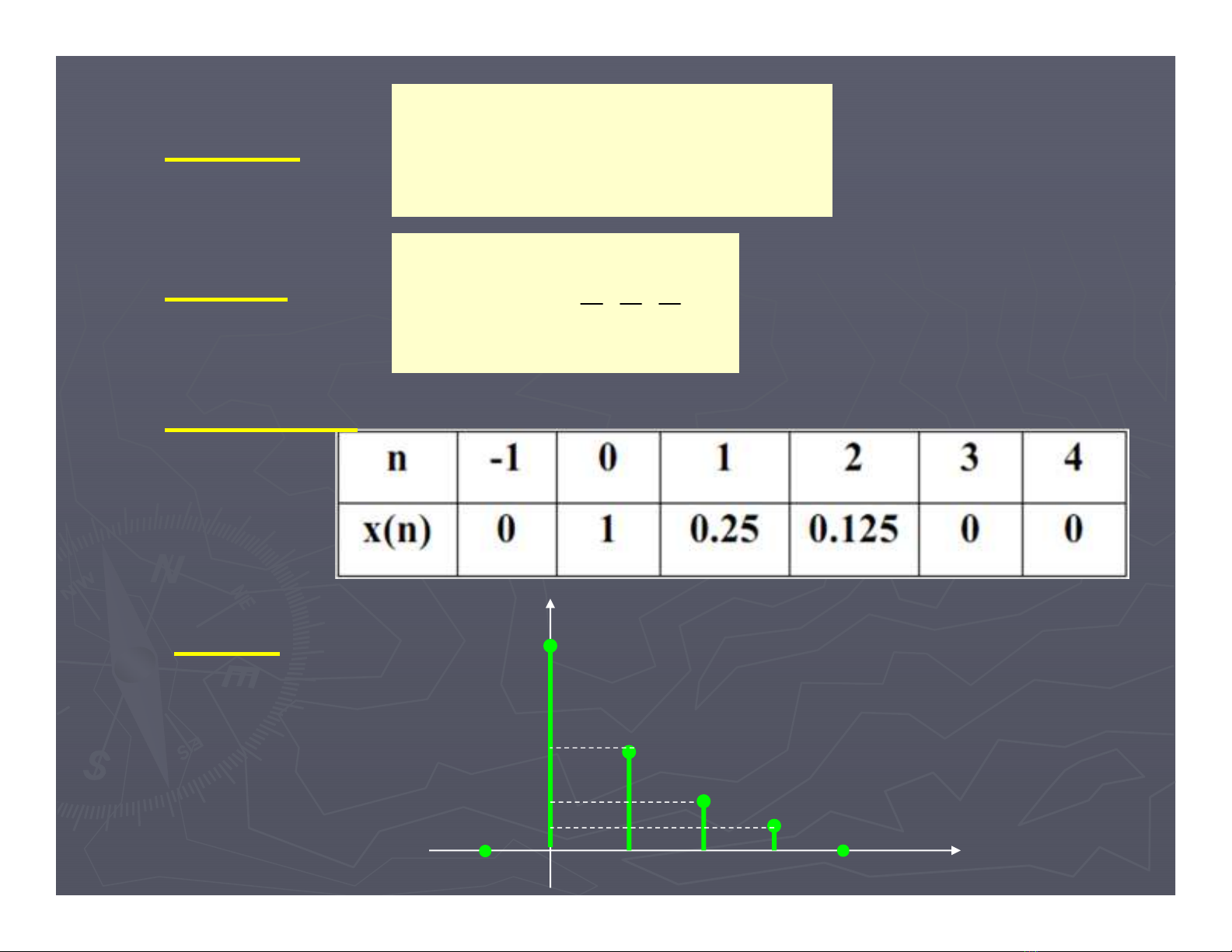
Dãy số:111
() 0,1, , , ,0
248
xn ↑
⎧
⎫
⎪
⎪
=
⎨
⎬
⎪
⎪
⎩⎭
↑ -Gốc thời gian n=0
Đồ thị:
Hàm số:
⎩
⎨
⎧≤≤
=:
n :).(
)n(x
n
0
3050
n còn lại
n
x(n)
0 1 2 3 4
1
0.5
0.25
0.125
Dạng bảng:
111
() 0,1, , , ,0
248
xn ↑
⎧
⎫
⎪
⎪
=
⎨
⎬
⎪
⎪
⎩⎭
2.1.2 MỘT SỐ TÍN HIỆU RỜI RẠC CƠ BẢN
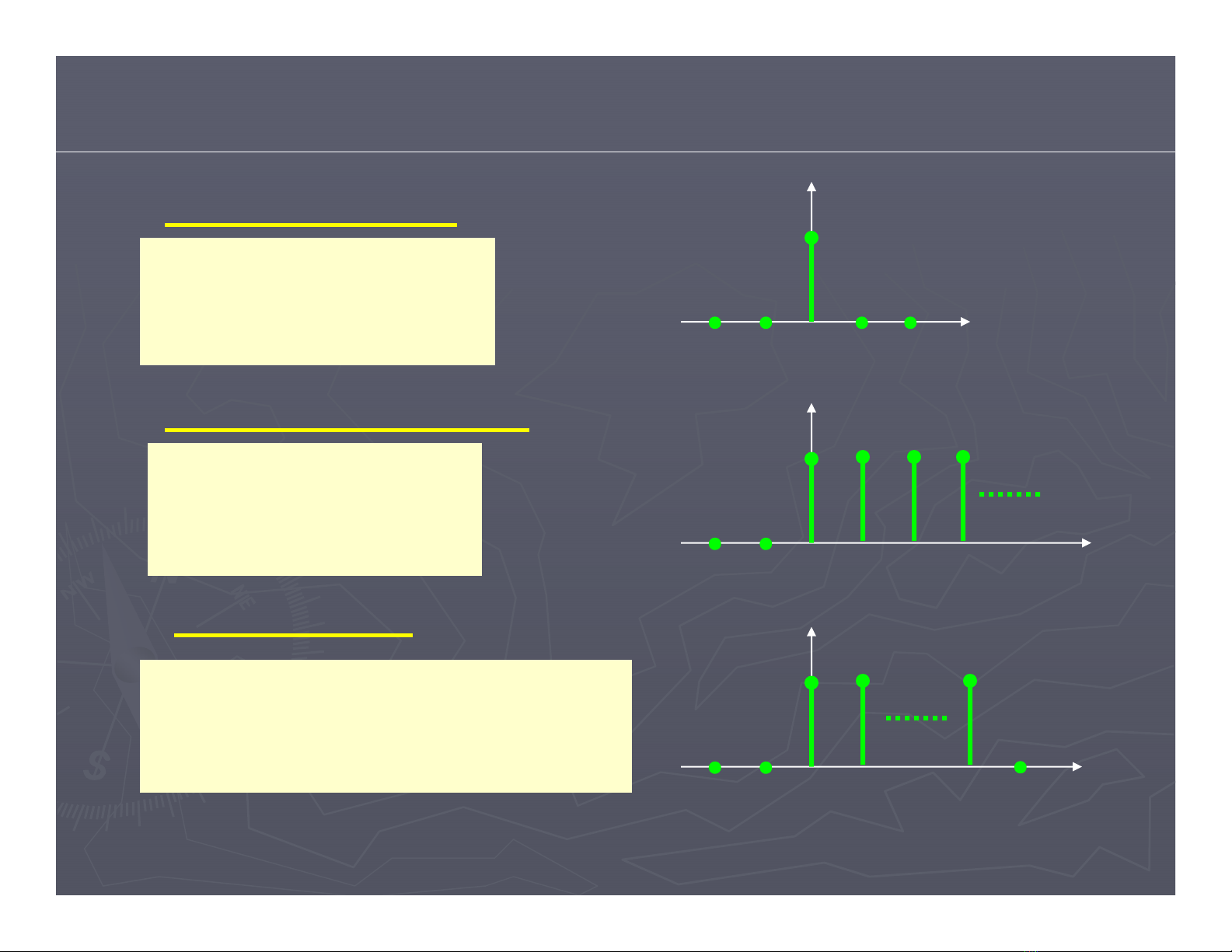
Dãy xung đơn vị:
:0
0 :1
)( ⎩
⎨
⎧=
=n
n
δ
n còn lại-2 -1 0 1 2
1
n
δ(n)
Dãy nhảy bậc đơn vị:
0 :0
0 :1
)( ⎩
⎨
⎧
<
≥
=n
n
nu
-2 -1 0 1 2 3
1
n
u(n)
Dãy chữ nhật:
-2 -1 0 1 N-1 N
1
n
rectN(n)
:
1-N :
)( ⎩
⎨
⎧≥≥
=n
n
nrectN0
01
còn lại