CHƯƠNG II: BIỂU DIỄN TÍN HIỆU
VÀ HỆ THỐNG RỜI RẠC TRONG
MIỀN Z
2.1. BIẾN ĐỔI Z (ZT: Z TRANSFORM)
2.1.1. Định nghĩa biến đổi z
Định nghĩa: Biến đổi z của một dãy x(n) được định nghĩa như sau:
n
n
X z x n z

Ký hiệu bởi toán tử:
ZT x n X z


ZT
x n X z
Trong định nghĩa trên, nếu đổi cận n=0 ta có biến đổi z 1 phía:
0
n
n
X z x n z
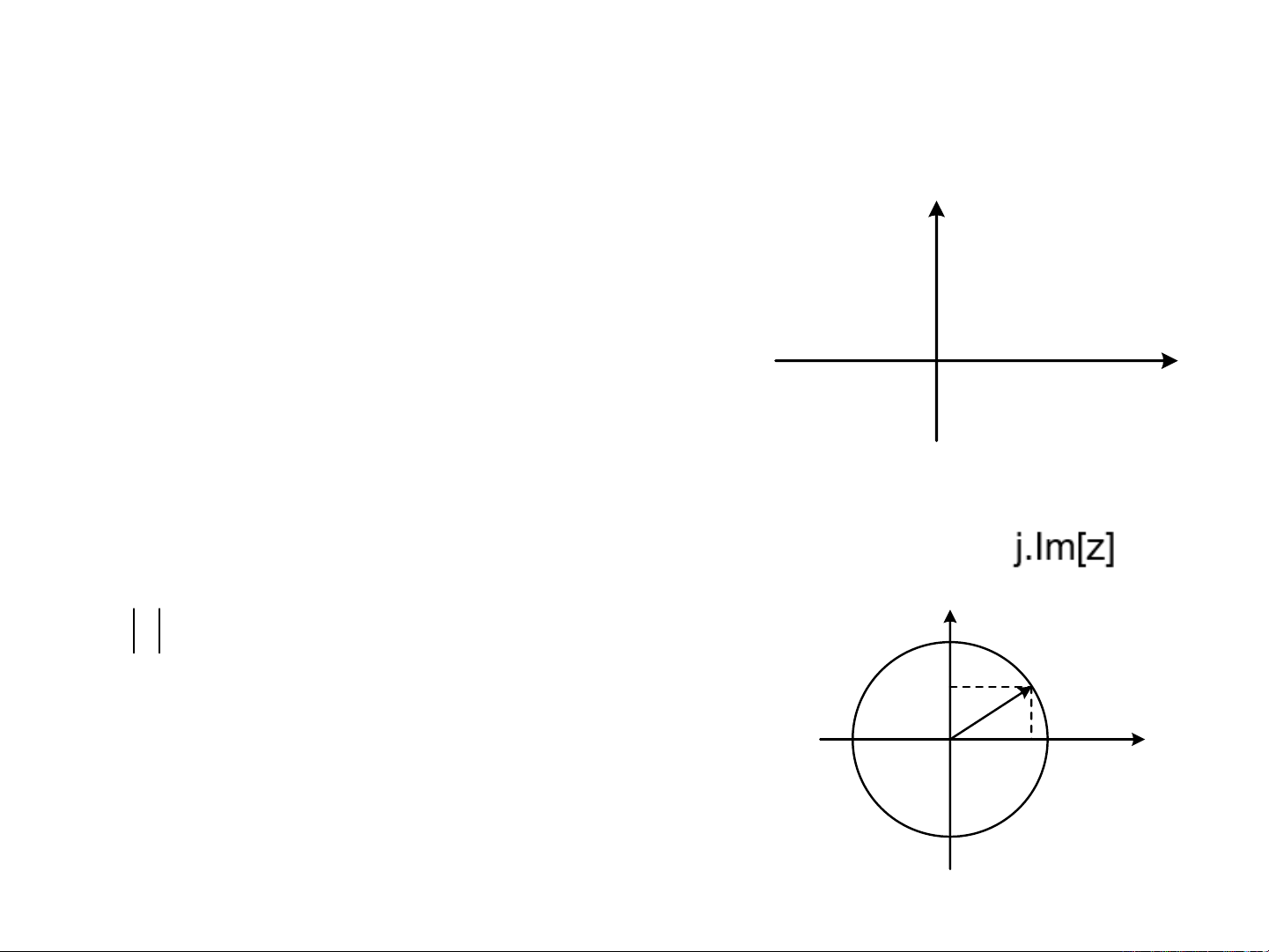
Biểu diễn theo phần thực, phần ảo Re[z], Im[z]
z = Re[z] + j.Im[z]
Im[z]
Re[z]
0
MÆt ph¼ng Z
Biểu diễn theo tọa độ cực:
cos sin cos sin Re Im
j
z re r j r j z z
Im[z]
Re[z]
0
r
Re
Im
ta có vòng tròn đơn vị.
Mặt phẳng Z
jrsin
Ví dụ biến đổi z
1
x n n
41
2
n
x n u n



21x n n

52n
x n u n
31x n n

0
11 1. 1
nn
nn
X z ZT x n x n z n z z






11
22 1 1.
n
n
X z ZT x n n z z z



1
33 1 1.
n
n
X z ZT x n n z z z


1
400
1 1 1
2 2 2

n n n
nn
n n n
X z u n z z z
1
1 1 1 1
11
2 2 2
zz
z
1
55 1
00
1
2 2 2 12


n
n n n n
n n n
X z ZT x n u n z z z z
Tìm biến đổi zcủa:
Giải:
2.1.2. Miền hội tụ của biến đổi z
Định nghĩa:
Tập hợp tất cả các giá trị của zmà tại đó chuỗi
n
n
X z x n z

hội tụ được gọi là miền hội tụ của biến đổi z.
Ký hiệu:RC:miền hội tụ (Region of Convergence)
Ví dụ:Hãy tìm miền hội tụ của biến đổi z trong ví dụ trước:
1
RC X z


,
3


RC X z
Toàn bộ mặt phẳng z
2
RC X z


: Toàn bộ mặt phẳng z trừ gốc tọa độ z = 0
Im[z]
Re[z]
0
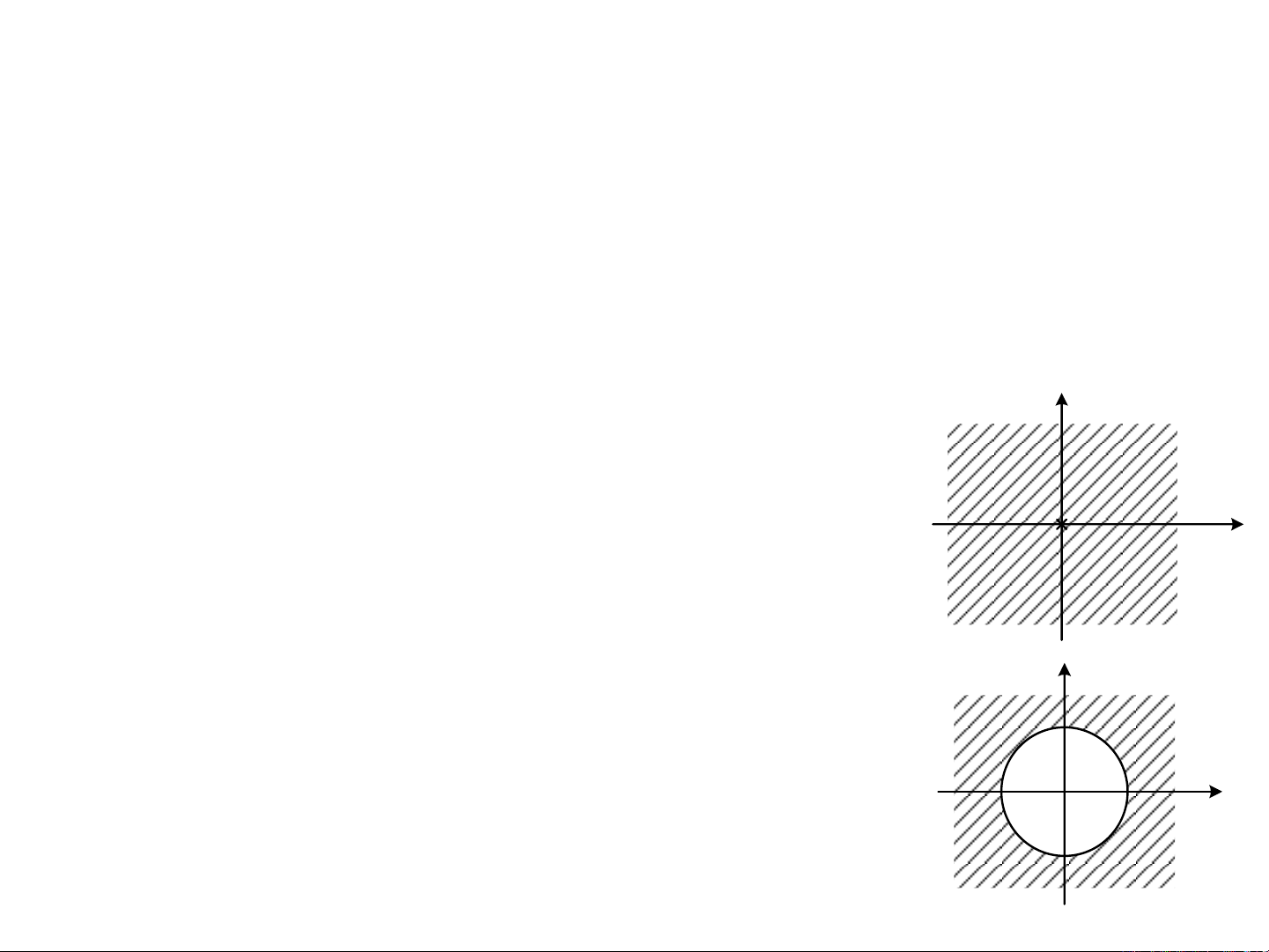
4
RC X z


:Ngoài vòng tròn bán kính ½
Im[z]
Re[z]
01/2
1/2
-1/2
-1/2
5


RC X z
:Ngoài vòng tròn bán kính 2