ET4020 - Xử lý tín hiệu số
Chương 2: Các phép biến đổi Fourier
TS. Đặng Quang Hiếu
http://dsp.edabk.org
Trường Đại học Bách Khoa Hà Nội
Viện Điện tử - Viễn thông
Năm học 2012 - 2013
Outline
Biến đổi Fourier
Chuỗi Fourier rời rạc cho dãy tuần hoàn
Biến đổi Fourier rời rạc
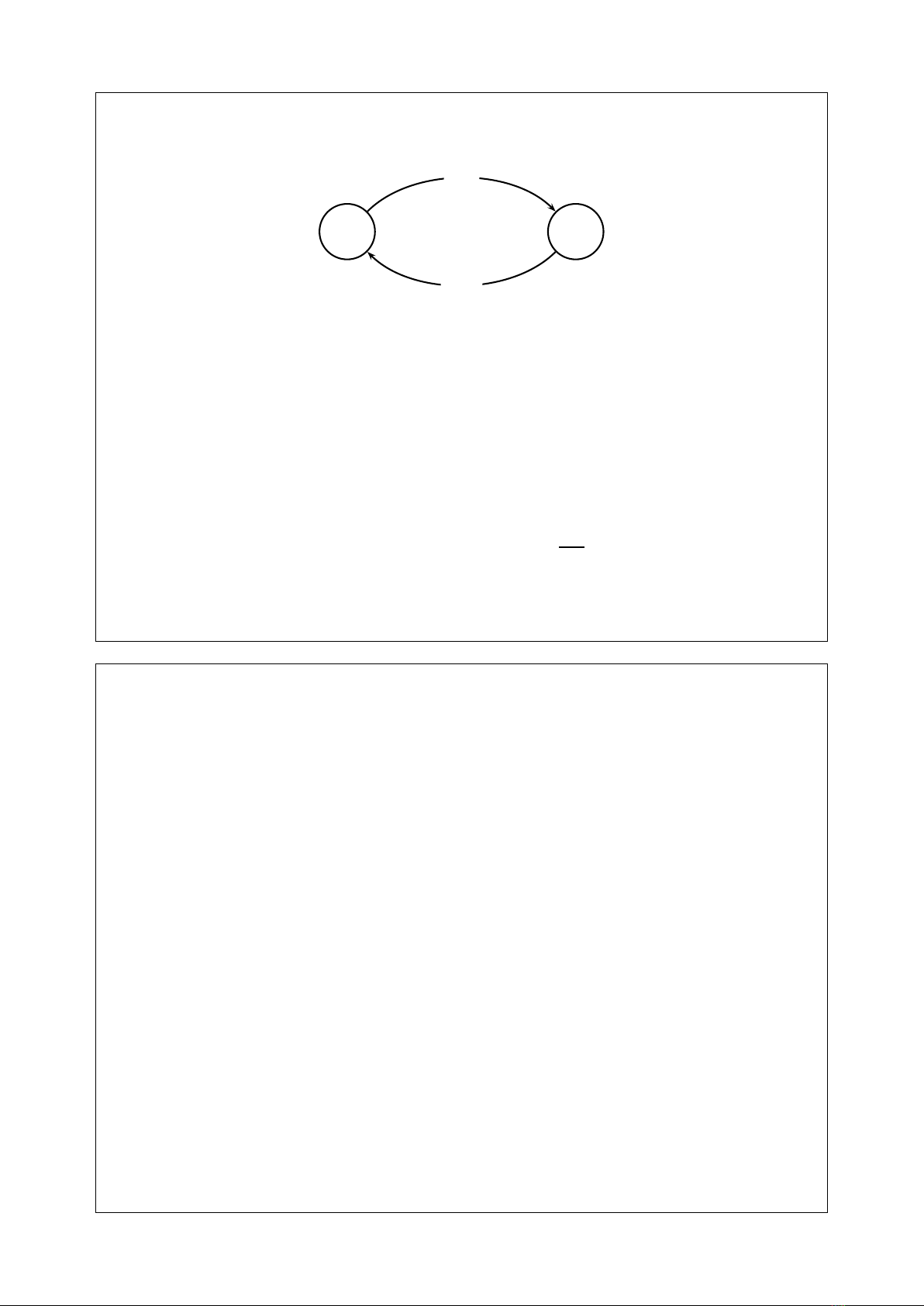
Biến đổi Fourier
nω
FT
IFT
x(n)FT
−−→ X(ejω) = FT{x(n)}=
∞
X
x=−∞
x(n)e−jωn
◮Tuần hoàn với chu kỳ 2π
◮Phổ biên độ: |X(ejω)|, và phổ pha: arg{X(ejω)}.
◮Biến đổi ngược:
X(ejω)IFT
−−−→ x(n) = IFT{X(ejω)}=1
2πZπ
−π
X(ejω)ejωndω
Các ví dụ về FT
1. Tìm X(ejω),|X(ejω)|và arg{X(ejω)}của các dãy sau đây:
(a) x(n) = δ(n)
(b) x(n) = δ(n−2)
(c) x(n) = δ(n−2)−δ(n)
(d) x(n) = rectN(n)
(e) x(n) = (0.5)nu(n)
(f) x(n) = u(n)
2. Xét bộ lọc thông thấp lý tưởng có đáp ứng tần số (trong một
chu kỳ) như sau:
Hlp(ejω) = 1,|ω| ≤ ωc
0, ωc<|ω| ≤ π
(a) Hãy tìm đáp ứng xung hlp (n)của bộ lọc này.
(b) Giải bài toán cho trường hợp bộ lọc thông cao
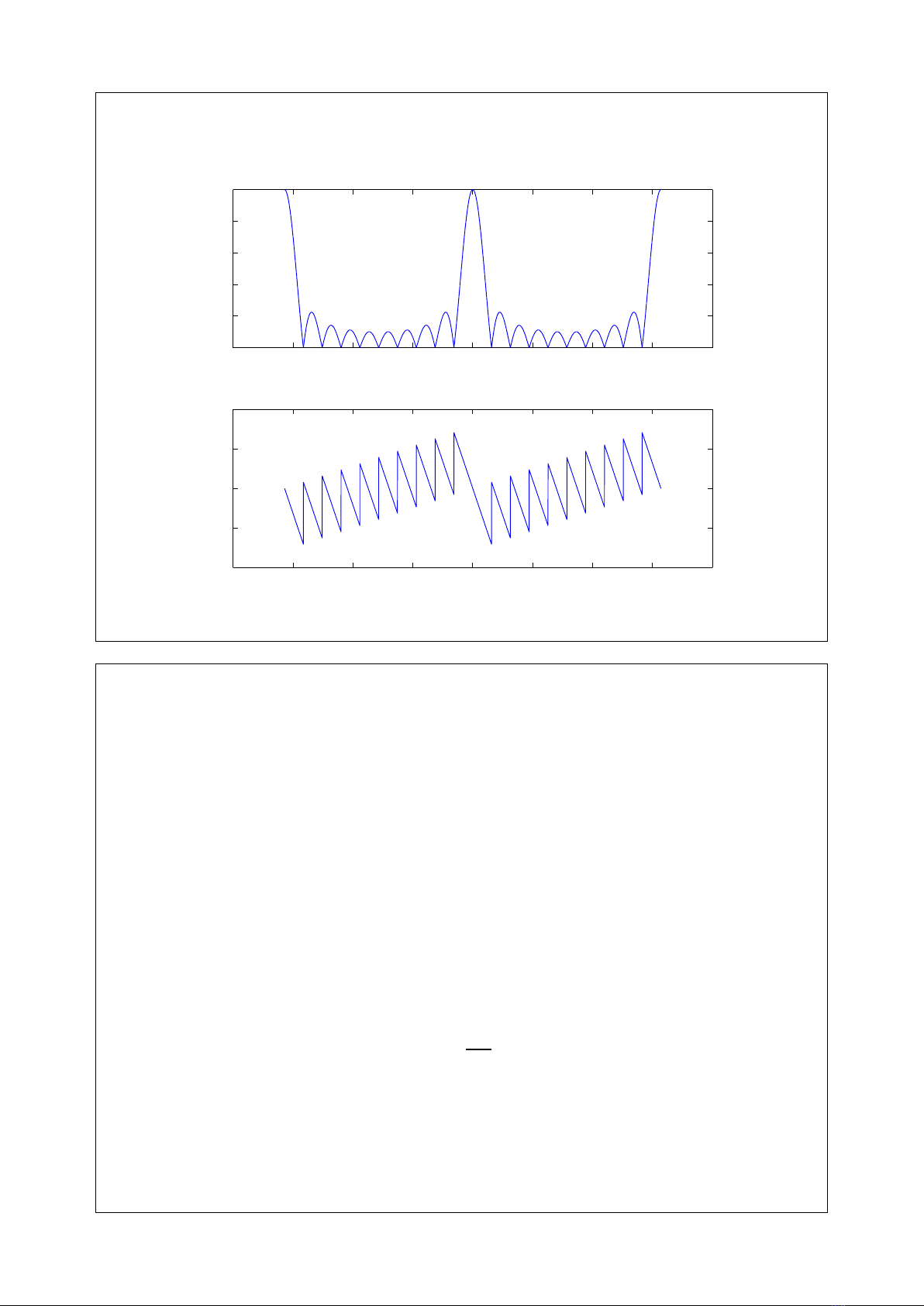
Phổ biên độ và phổ pha của rect10(n)
−8 −6 −4 −2 0 2 4 6 8
0
2
4
6
8
10
ω
|X(jω)|
−8 −6 −4 −2 0 2 4 6 8
−4
−2
0
2
4
ω
arg{X(jω)}
Các tính chất
◮Quan hệ với biến đổi z:
X(ejω) = X(z)|z=ejω
◮Điều kiện hội tụ:
∞
X
n=−∞
|x(n)|<∞
Một hệ thống LTI có đáp ứng tần số khi và chỉ khi nó ổn định.
◮Tuyến tính, dịch thời gian, dịch tần số, chập, v.v.
◮Các tính chất đối xứng
◮Quan hệ Parseval
∞
X
n=−∞
|x(n)|2=1
2πZπ
−π
|X(ejω)|2dω
◮Định lý Wiener - Khintchine: Nếu x(n)∈Rthì
FT{rxx (n)}=SXX (ejω) := |X(ejω)|2
trong đó SXX (ejω)là phổ mật độ năng lượng của x(n).
Outline
Biến đổi Fourier
Chuỗi Fourier rời rạc cho dãy tuần hoàn
Biến đổi Fourier rời rạc
Khái niệm dãy tuần hoàn
˜x(n) = ˜x(n−N),∀n
◮Chu kỳ N∈Z→ký hiệu ˜x(n)N.
◮Tồn tại khai triển Fourier
◮Khác hệ số Nso với khái niệm chuỗi Fourier cho tín hiệu tuần
hoàn trong môn Tín hiệu và hệ thống!
Định nghĩa cặp chuỗi Fourier rời rạc cho dãy tuần hoàn
˜
X(k) =
N−1
X
n=0
˜x(n)e−j2π
Nkn
˜x(n) = 1
N
N−1
X
k=0
˜
X(k)ej2π
Nkn
◮WN=e−j2π
N.
◮Biên độ và pha: |˜
X(k)|, arg{˜
X(k)}.
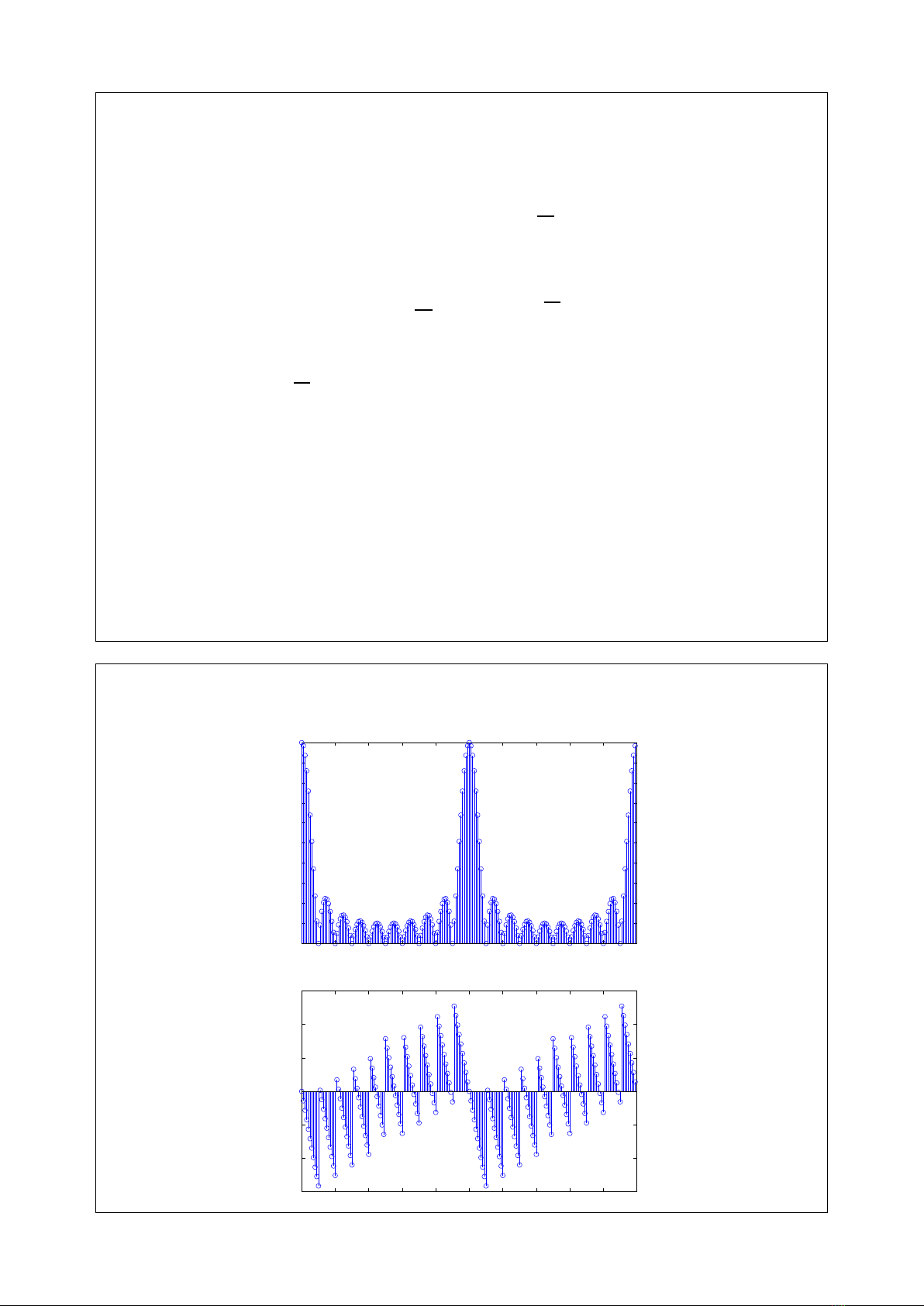
Ví dụ: Cho tín hiệu tuần hoàn ˜x(n)với chu kỳ N:
˜x(n) = 1, ℓN≤n≤ℓN+M−1,∀n∈Z,M<N
0,ncòn lại
Hãy tìm ˜
X(k),|˜
X(k)|,arg{˜
X(k)}.
Khi N=100,M=10
−100 −80 −60 −40 −20 0 20 40 60 80 100
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
k
|X[k]|
−100 −80 −60 −40 −20 0 20 40 60 80 100
−3
−2
−1
0
1
2
3
k
arg{X[k]}