π
b
1
≡b
2
k
n
b
3
b
3
d
3
≡d
4
n
e
4
e
4
≡ e
5
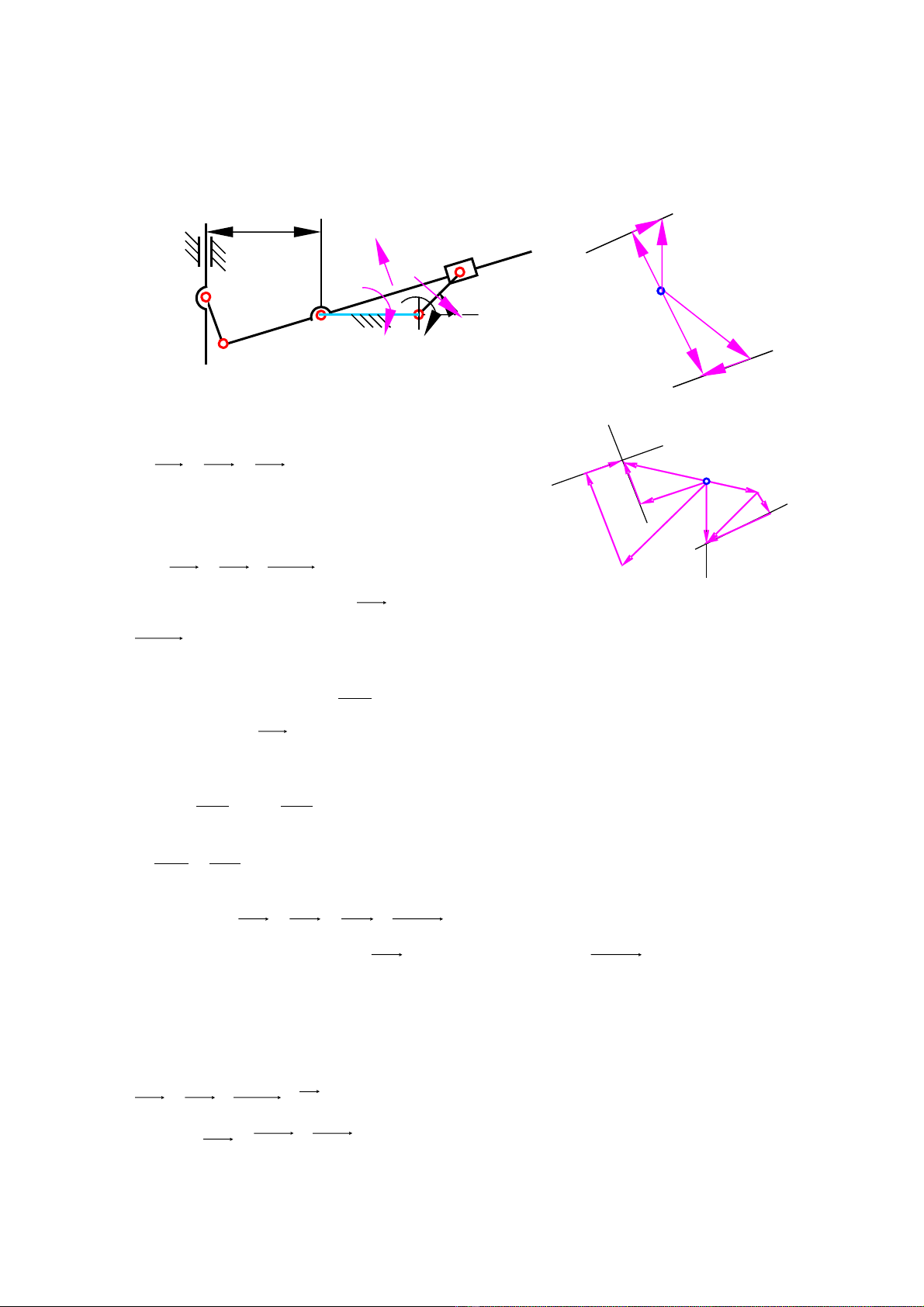
Hình 2.1c
CH NƯƠ G 2: PHÂN TÍCH Đ NG H C C C U PH NG LO I 2Ộ Ọ Ơ Ấ Ẳ Ạ
1) Xác đ nh v n t c và gia t c c a dao bào E trong c c u máy bào x c (hình 2.1a) khi tayị ậ ố ố ủ ơ ấ ọ
quay 1 quay đ u v i v n t c góc ề ớ ậ ố
1
110 −
=s
ω
t i v trí ạ ị
o
45
1=
ϕ
. Cho bi t kích th c cácế ướ
khâu c a c c u: ủ ơ ấ
;
mll CDAC 3,0==
; a = 0,35m.
Hình 2.1a Hình 2.1b
B1 ≡ B2 ≡ B3, khâu 1 n i v i khâu 2 b ng kh pố ớ ằ ớ
quay, khâu 2 n i v i khâu 3 b ng kh p tr tố ớ ằ ớ ượ
321 BBB VVV ≠=
Giá tr : ị
smlVV ABBB /22,0.10.
1
21 ====
ω
, có
ph ng vuông góc v i khâu AB, chi u theo chi u v n t cươ ớ ề ề ậ ố
góc khâu 1.
2323 BBBB VVV +=
(1)
Trong ph ng trình (1), ươ
3
B
V
vuông góc v i BC,ớ
23 BB
V
có ph ng song song v i BC. ươ ớ
Ch n t l xích đ v : ọ ỷ ệ ể ẽ
)//(
2
2mmsm
pb
VB
V=
µ
. Ho đ v n t c đ c v nh hình 2.1b.ạ ồ ậ ố ượ ẽ ư ở
Đo giá tr véc t ( ị ơ
3
pb
) bi u di n v n t c đi m Bể ễ ậ ố ể 3 và nhân v i t l xích ta thu đ c giá tr th c v nớ ỷ ệ ượ ị ự ậ
t c đi m Bố ể 3.
BC
V
BC
B
l
pb
l
V3
3.
3
µω
==
Vì
CD
BC
D
B
l
l
V
V=
3
3
, t đó suy ra v n t c c a đi m Dừ ậ ố ủ ể
E4 ≡ E5 và khâu 4 n i v i khâu 5 b ng kh p quay:ố ớ ằ ớ
44445 DEDEE VVVV +==
(2)
Trong ph ng trình này: ươ
4
E
V
có ph ng th ng đ ng. ươ ẳ ứ
44 DE
V
có ph ng vuông góc v iươ ớ
DE. Ho đ đ c v nh hình 2.1b.ạ ồ ượ ẽ ư ở
Ta đo đo n ạ
5
pe
và nhân v i t l xích đã ch n s có giá tr v n t c khâu 5, chi u đi lên.ớ ỷ ệ ọ ẽ ị ậ ố ề
T ng t ta cũng xác đ nh đ c gia t c:ươ ự ị ượ ố
22
1/202,0.100
21 smlaa ABBB ====
ω
có chi u h ng t B đi vào Aề ướ ừ
k
BBBB aaaa ++= 2323
M t khác ặ
τ
CB
n
CB
Baaa 33
3+=
, do v yậ
A
B
C
D
E
1
2
3
4
5
ϕ1
ω
a
p
b1≡b2
b3
d3≡d4
e5≡e4
ω
3
ak
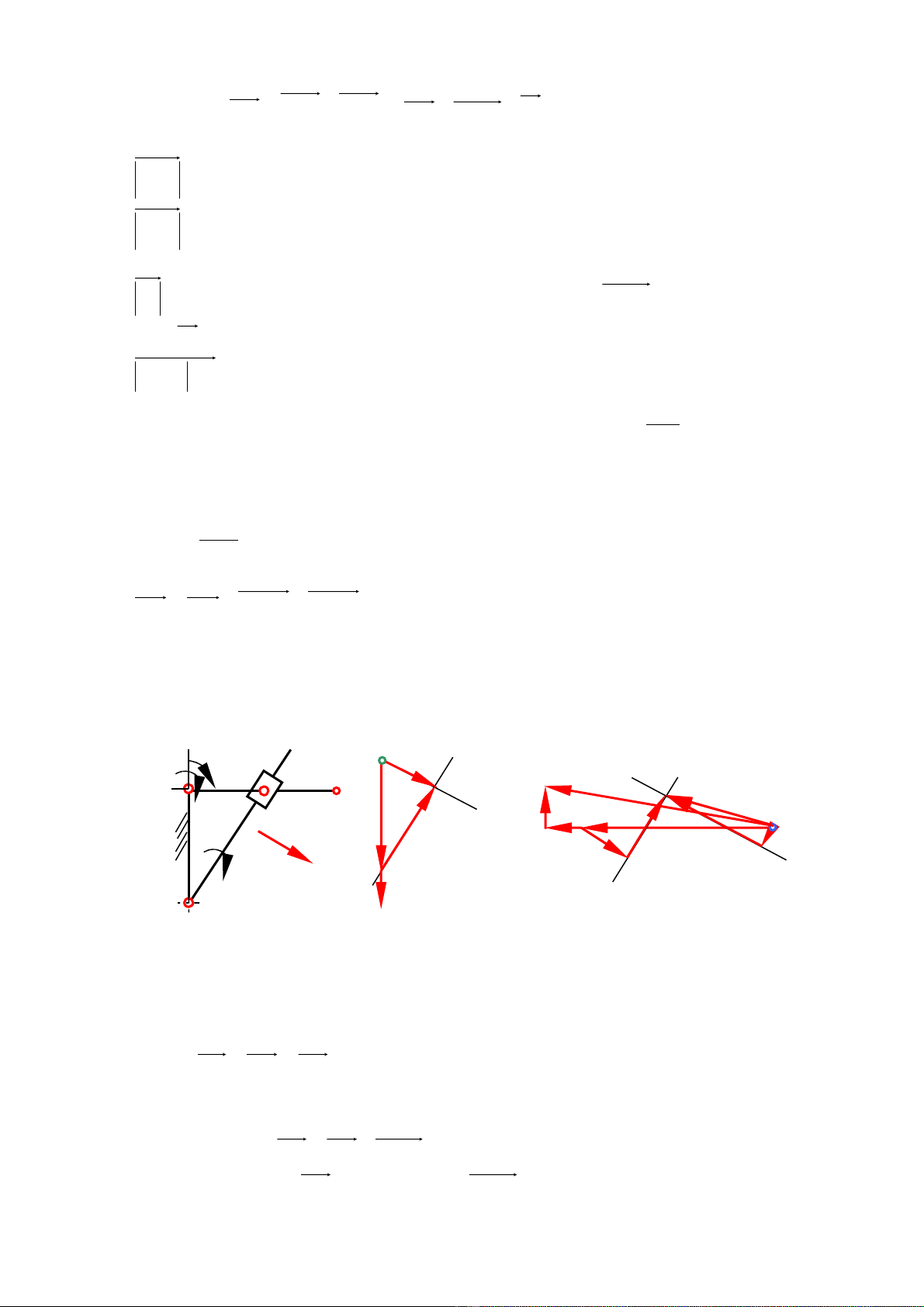
τ
CB
n
CB
Baaa 33
3+=
=
k
BBB aaa ++ 232
(3)
Trong ph ng trình (3) :ươ
AB
n
CB la .
2
3
3
ω
=
; đã xác đ nh v giá tr có ph ng chi u h ng t B đi vào C.ị ề ị ươ ề ướ ừ
?.
3
3== AB
CB la
ε
τ
; ph ng vuông góc v i BC.ươ ớ
3232 .2.2 23 bbVa VBB
k
µωω
==
; Ph ng chi u l y theo chi u ươ ề ấ ề
23 BB
V
quay đi m t góc 90ộ0 theo
chi u ề
3
ω
.
?
23 =
BB
a
, ph ng song song v i BC.ươ ớ
Ph ng trình (3) ch t n t i 2 n s , ch n t l xích ho đ gia t c: ươ ỉ ồ ạ ẩ ố ọ ỷ ệ ạ ồ ố
)//( 2
2
2mmsm
b
aB
a
π
µ
=
.
Cách gi i đ c trình bày trên hình 2.1cả ượ
Các giá tr đ c đo tr c ti p trên các véc t bi u di n t ng ng sau đó nhân v i t l xích đã ch n.ị ượ ự ế ơ ể ễ ươ ứ ớ ỷ ệ ọ
Xác đ nh gia t c góc khâu 3:ị ố
BC
n
al
bb 3
3
3
µε
=
Xác đ nh gia t c đi m Dị ố ể 3 cũng b ng ph ng pháp đ ng d ngằ ươ ồ ạ
τ
4444
44 DE
n
DE
DE aaaa ++=
(4)
Cách lý lu n cũng t ng t . Cách gi i trình bày trên hình 2.1cậ ươ ư ả
2) Tính v n t c và gia t c đi m Dậ ố ố ể 2 (∠ DBC = 1200) trên con tr t 2 c a c c u cu lít t i v tríượ ủ ơ ấ ạ ị
ϕ
1=900. Tay quay AB quay đ u v i v n t c góc ề ớ ậ ố ω1 = 20s-1. Cho bi t kích th c các khâu c aế ướ ủ
c c u: ơ ấ lAB = lBD = 0,5lBC = 0,2m.
Hình 2.2a Hình 2.2b Hình 2.2c
S t ng quan kích th c đã cho ta th y r ng tam giác ABC là n a tam giác đ u,ự ươ ướ ấ ằ ử ề
(∠ABC=600) BD thu c khâu 2. Đ xác đ nh v n t c đi m D, tr c tiên ta ph i bi t v n t c đi m Bộ ể ị ậ ố ể ướ ả ế ậ ố ể 2 và
v n t c góc khâu 2, sau áp d ng đ nh lý h p v n t c s thu đ c v n t c đi m D. Khâu 2 tr t trongậ ố ụ ị ợ ậ ố ẽ ượ ậ ố ể ượ
khâu 3 và quay theo khâu 3 cho nên t c đ góc khâu 2 cũng chính là t c đ góc khâu 3.ố ộ ố ộ
B1 ≡ B2 ≡ B3, khâu 1 n i v i khâu 2 b ng kh p quay, khâu 2 n i v i khâu 3 b ng kh p tr tố ớ ằ ớ ố ớ ằ ớ ượ
321 BBB VVV ≠=
Giá tr : ị
smlVV ABBB /42,0.20.
1
21 ====
ω
, có ph ng vuông góc v i khâu AB, chi u theoươ ớ ề
chi u v n t c góc khâu 1.ề ậ ố
2323 BBBB VVV +=
(1)
Trong ph ng trình (1), ươ
3
B
V
vuông góc v i BC, ớ
23 BB
V
có ph ng song song v i BCươ ớ
AB
C
D
2
1
3
ω
ϕ1
ω
p
b1 ≡ b2
b3
d2
ak
ε3
b1 ≡ b2
b3
k
b3
n
π
d2
n
d2
Trong tr ng h p đ c bi t này ta không c n ch n t l xích. Ho đ v n t c đ c v nh hìnhườ ợ ặ ệ ầ ọ ỷ ệ ạ ồ ậ ố ượ ẽ ư ở
2.2b.
Tam giác pb2b3 đ ng d ng v i tam giác BCA, ta tính đ c v n t c đi m bồ ạ ớ ượ ậ ố ể 3:
smVV BB /22/
23 ==
.
T c đ góc khâu 3 và khâu 2: ố ộ
srad
l
V
BC
B/5
4,0
2
3
32 ====
ωω
. Chi u đ c xác đ nh nh hình về ượ ị ư ẽ
2222 BDBD VVV +=
(2)
Trong ph ng trình (2) ta đã bi t v n t c đi m Bươ ế ậ ố ể 2 ,
smlV BDBD /12,0.5.
2
22 ===
ω
.
Chi u h ng t trên xu ng theo chi u ề ướ ừ ố ề ω2 và vuông góc v i BD. Ho đ đ c v ti p nh hìnhớ ạ ồ ượ ẽ ế ư ở
2.2b. Giá tr v n t c đi m D đ c tính:ị ậ ố ể ượ
smVVV BDBD /514
2222 =+=+=
T ng t ta cũng tính đ c gia t c đi m Dươ ự ượ ố ể 2:
321 BBB aaa ≠=
22
1/802,0.400.
21 smlaa ABBB ====
ω
kBBBB aaaa ++= 2323
τ
CB
n
CB
Baaa 33
3+=
kBBB aaa ++ 232
=
τ
CB
n
CB
aa 33 +
(2)
Trong ph ng trình trên (2) Ta có đ c:ươ ượ
2
B
a
: Đã xác đ nh; ị
23 BB
a
: Giá tr ch a bi t, ph ng song song v i BC.ị ư ế ươ ớ
2
3/32032.5.2.2 23 smVa BBk ===
ω
22
3
/104,0.25.
3smla
BC
n
CB
===
ω
?.
3
3
==
BC
CB
la
ε
τ
, có ph ng vuông góc v i BC.ươ ớ
Ph ng trình (2) t n t i 2 n s , Ho đ gia t c đ c v nh hình 2.1cươ ồ ạ ẩ ố ạ ồ ố ượ ẽ ư ở
Gia t c góc khâu 2 và khâu 3 đ c tính nh sau:ố ượ ư
BC
CB
l
a
τ
εε
3
32 ==
on
B
o
o
k
o
n
B
B
CB tga
a
a
aa 6060sin)
60sin60cos
(3
3
2
3+
+−=
τ
2
/63,47310
2
3
)40580( sm=+−−=
2
32 /075,119
4,0
63,47
3srad
l
a
BC
CB ====
τ
εε
τ
2222
22 BD
n
BD
BD aaaa ++=
(3)
Trong ph ng trình (3) Ta đã bi t:ươ ế
22
2/52,0.25.
22 smla BD
n
BD ===
ω
2
2/815,282,0.075,119.
2smla BD
BD ===
ε
τ
Ho đ gia t c đ c v trên hình 2,2cạ ồ ố ượ ẽ
Giá tr gia t c đi m D đ c tính: ị ố ể ượ
( )
22
2/27,88815,28580
2smaD=++=
3) Tính v n t c và gia t c khâu 3 c a c c u tính tang m t góc, n u tay quay AB quay đ u v iậ ố ố ủ ơ ấ ộ ế ề ớ
v n t c góc ậ ố ω= 10s-1, t i v trí ạ ị ϕ1 = 60o. Cho tr c h = 0,05m (hình 2.3a).ướ
Hình 2.3a Hình 2.3b Hình 2.3c
Vì khâu 3 chuy n đ ng t nh ti n, cho nên m i đi m trên khâu 3 đ u có v n t c và gia t c nhể ộ ị ế ọ ể ề ậ ố ố ư
nhau. Chúng ta đi xác đ nh v n t c và gia t c đi m Bị ậ ố ố ể 3 .
B1 ≡ B2 ≡ B3 . Khâu 1 n i v i khâu2 b ng kh p t nh ti n, khâu 2 n i v i khâu 3 b ng kh p quay:ố ớ ằ ớ ị ế ố ớ ằ ớ
321 BBB VVV =≠
smlV ABB /577,0
3
3
10.05,0.
3
3
2.
1
1====
ω
1212 BBBB VVV +=
(1)
//BC //AB
Ph ng trình ch t n t i hai n s là giá tr v n t c đi m Bươ ỉ ồ ạ ẩ ố ị ậ ố ể 2 và v n t c t ng đ i gi a 2 đi m Bậ ố ươ ố ữ ể 1
và B2. Ho đ véc t v n t c đ c v nh hình 2.3b.ạ ồ ơ ậ ố ượ ẽ ư
V n t c đi m Bậ ố ể 2 đ c tính nh sau: ượ ư
./67,0
3
3
222 smVV BB ==
chi u đ c xác đ nh nh trên hoề ượ ị ư ạ
đ v n t c (hình 2.3b).ồ ậ ố
T ng t gia t c ta cũng có: ươ ự ố
321 BBB aaa =≠
22
1/
3
3
1005,0.
3
3
2.100.
1smla ABB ===
ω
kBBBB aaaa ++= 1212
//BC // AB
:
k
a
có giá tr là ị
2
1/
3
3
10
6
3
.10.2..2 12 smV BB ==
ω
.
Ph ng chi u theo chi u c a ươ ề ề ủ
12 BB
V
quay đi m t góc 90ộo theo chi u ềω1 . Ho đ gia t cạ ồ ố
đ c v nh hình 2.3c. Giá tr gia t c khâu 3 đ c tính:ượ ẽ ư ở ị ố ượ
2
/7,6
3
3
.
3
3
.10.2
3
3
2
32 smaaa kBB ====
4) Tính v n t c và gia t c đi m C (hình 2.4a), v n t c góc và gia t c góc c a các khâu 2 và 3ậ ố ố ể ậ ố ố ủ
trong c c u 4 khâu b n l t i v trí ơ ấ ả ề ạ ị ∠ABC = ∠BCD = 90o , n u tay quay AB quay đ u v iế ề ớ
v n t c góc ậ ố ω1= 20s-1. Cho tr c kích th c c a các khâu ướ ướ ủ 4lAB = lBC = lCD = 0,4m.
p
b1b2, b3
A
B
C
h
ϕ1
1
2
3
ak
b1
k
b3, b2
π
p
b1, b2, c2,c3
b1, b2
c2,c3
π
A
B
C
D
12
3
ω1
ω3
ω2
Hình 2.4a Hình 2.4b Hình 2.4c
B1 ≡ B2. Khâu 1 n i v i khâu 2 b ng kh p quay:ố ớ ằ ớ
21 BB VV =
smlV ABB /21,0.20.
1
1===
ω
T ng t : Cươ ự 2 ≡ C3 và
32 CC VV =
2222 BCBC VVV +=
(1)
⊥CD ⊥BC
Ph ng trình ch t n t i hai n s là giá tr v n t c đi m Cươ ỉ ồ ạ ẩ ố ị ậ ố ể 2 và v n t c t ng đ i gi a 2 đi m Cậ ố ươ ố ữ ể 2
và B2. Ho đ véc t v n t c đ c v nh hình 2.3b.ạ ồ ơ ậ ố ượ ẽ ư
T ho đ ta th y răng v n t c đi m C và v n t c đi m B thu c khâu 2 là b ng nhau, do v y khâu 2ừ ạ ồ ấ ậ ố ể ậ ố ể ộ ằ ậ
chuy n đ ng t nh ti n t c th i: ể ộ ị ế ứ ờ ω2 = 0.
V n t c góc khâu 3: ậ ố
srad
l
V
CD
C/5
4,0
2
3
3===
ω
Chi u đ c xác đ nh theo chi u Về ượ ị ề C3 nh hình v .ư ẽ
Xác đ nh gia t c:ị ố
21 BB aa =
22
1/401,0.400.
1smla ABB ===
ω
ττ
2222
2
33
32 BC
n
BC
B
DC
n
DC
CC aaaaaaa ++=+==
(2)
Trên ph ng trình 2:ươ
n
DC
a3
: Có giá tr b ng: ị ằ ω23 . lCD = 25 . 0,4 = 10m/s2
τ
DC
a3
: Giá tr ch a bi t, có ph ng vuông góc v i CDị ư ế ươ ớ
n
BC
a22
: có giá tr b ng 0 vì ị ằ ω2 = 0.
τ
22 BC
a
: Giá tr ch a bi t, có ph ng vuông góc v i BC.ị ư ế ươ ớ
Ph ng trình ch còn t n t i 2 n s là giá tr c a 2 gia t c ti p. Cách gi i đ c trình bày trênươ ỉ ồ ạ ẩ ố ị ủ ố ế ả ượ
hình 2.4c.
Gia t c Đi m C bây gi ch t n t i gia t c pháp có chi u h ng t C đi vào D và có giá tr làố ể ờ ỉ ồ ạ ố ề ướ ừ ị
10m/s2. Gia t c ti p b ng 0.ố ế ằ
Gia t c ti p trong chuy n đ ng t ng đ i gi a đi m Cố ế ể ộ ươ ố ữ ể 2 đ i v i đi m Bố ớ ể 2 là
τ
22 BC
a
đ c bi uượ ể
di n b i véc t ễ ở ơ
22cb
có giá tr là : 40 – 10 = 30m/sị2.
Gia t c góc khâu2 đ c xác đ nh: ố ượ ị ε2 = 30 / 0,4 = 75rad/s2. chi u xác đ nh nh trên hình v .ề ị ư ẽ
5) Tính v n t c và gia t c đi m C và v n t c góc và gia t c góc c a thanh truy n 2 trong cậ ố ố ể ậ ố ố ủ ề ơ
c u tay quay con tr t (hình 1.5a) khi tay quay và thanh truy n th ng hàng. Bi t tay quayấ ượ ề ẳ ế
AB quay đ u v i v n toccs góc ề ớ ậ ω1 = 20s-1 và kích th c các khâu : 2lướ AB = lBC = 0,2m.
π
b1, b2
c2
n, c2, c3
p
b1, b2
c2, c3
ABC
123
ω
ω