
Khoa Mạng máy tính & Truyền thông - UIT
BÁO CÁO BÀI THỰC HÀNH SỐ 3
Public-key Cryptography -
RSA
Môn học: An toàn mạng máy tính
Lớp: NT101.O11.MMCL
Giảng viên hướng dẫn
Nguyễn Xuân Hà
Sinh viên thực hiện
Lê Huỳnh Quang Vũ (21522797)
Nguyễn Trọng Phúc (21522476)
Trần Nguyễn Quốc Bảo (21521865)
Mức độ hoàn thành
Hoàn thành
Thời gian thực hiện
23/10/2023 – 30/10/2023
Tự chấm điểm
10/10
3
Lab

Lab 3: RSA Public-Key Encryption
2
A. CÁC BƯỚC THỰC HÀNH
B. TRẢ LỜI CÁC CÂU HỎI
1. Number Theory
Task 1.1
Write a program (with your own programming language) to fulfil the following
requirements:
1. Prime number:
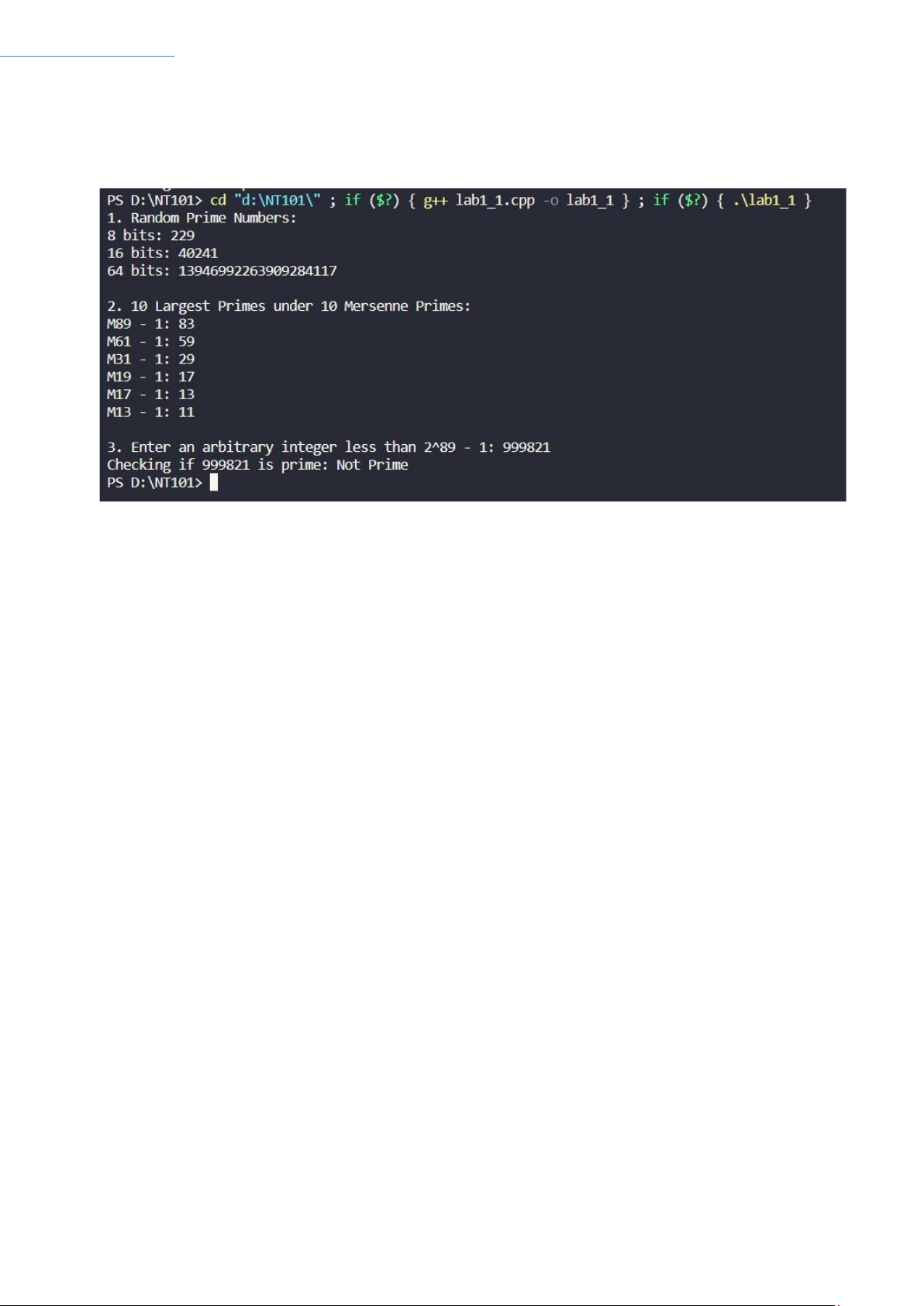
• Generate a random prime number with 8 bits, 16 bits, 64 bits
• Determine the 10 largest prime numbers under 10 first Mersenne
prime numbers.
• Check if an arbitrary integer less than 289 -1 is prime or not
2. Determine the greatest common divisor (gcd) of 2 arbitrary “large” integers
(which are as large as possible that you can handle)
3. Compute the modular exponentiation ax mod p. Your program should be able
to compute in case of “large” exponents (x>40), for example, 740 mod 19
Task 1.1.1:
Cách giải:
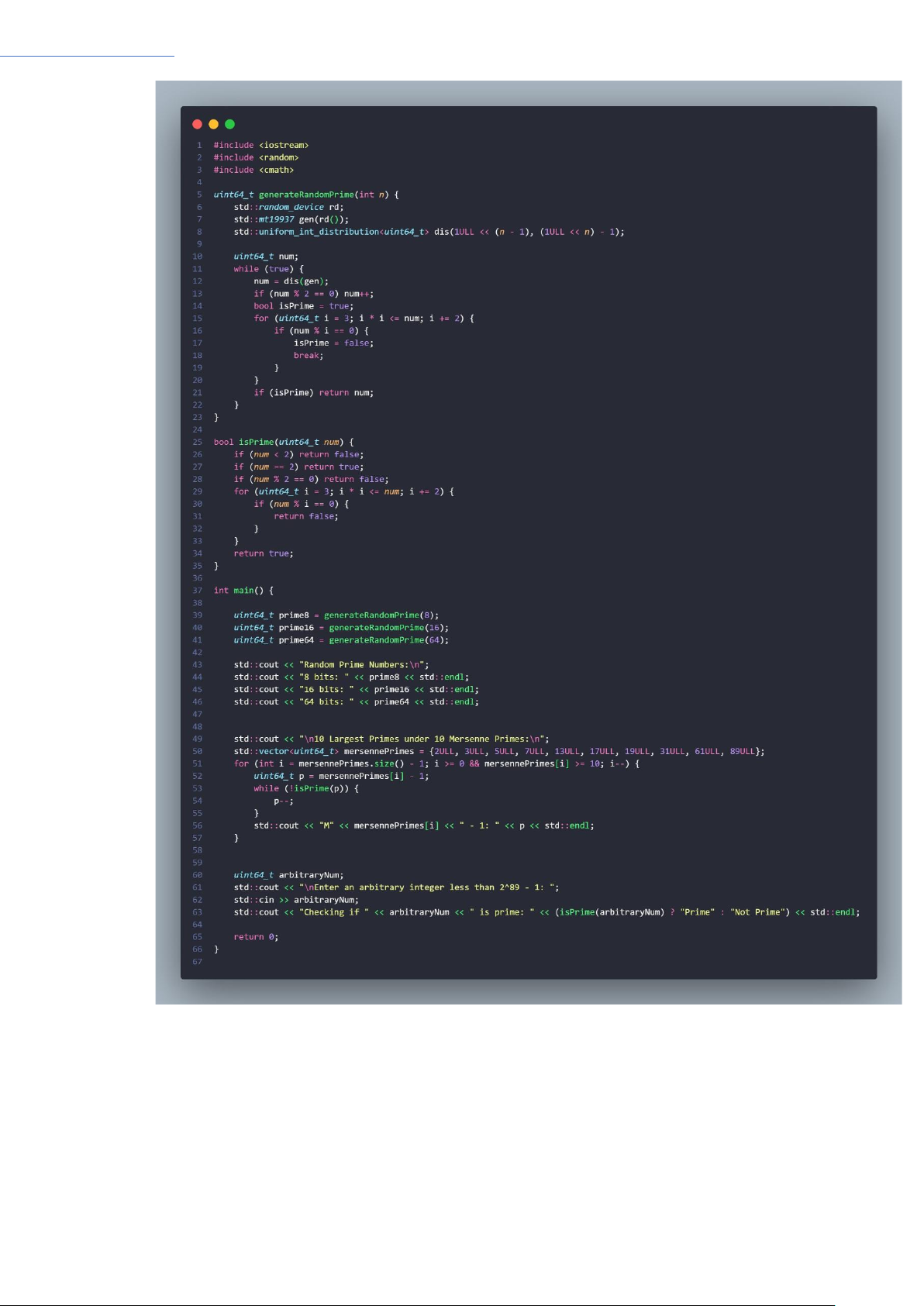
1. Hàm generateRandomPrime:
− Hàm này tạo một số nguyên tố ngẫu nhiên có n bit bằng cách sử dụng một phân phối đều với
giới hạn từ (1ULL << (n - 1)) đến (1ULL << n) - 1.
− Số ngẫu nhiên được tạo ban đầu, sau đó kiểm tra xem nó có phải là số chẵn không. Nếu là số
chẵn, nó được tăng thêm 1 để đảm bảo rằng nó là số lẻ.
− Sau đó, hàm kiểm tra tính nguyên tố của số ngẫu nhiên bằng cách kiểm tra xem nó có chia hết
cho bất kỳ số nguyên nào trong khoảng từ 3 đến căn bậc hai của nó hay không. Nếu không chia
hết cho bất kỳ số nào trong khoảng này, thì số đó được coi là số nguyên tố và trả về.
2. Hàm isPrime:
− Hàm này kiểm tra tính nguyên tố của một số được truyền vào.
− Nếu số đó nhỏ hơn 2, nó không phải là số nguyên tố và trả về false.
− Nếu số đó bằng 2, nó là số nguyên tố và trả về true.
− Nếu số đó là số chẵn khác 2, nó không phải là số nguyên tố và trả về false.
− Nếu số đó không phải là số chẵn và lớn hơn 2, thì hàm kiểm tra xem nó có chia hết cho bất kỳ
số nguyên nào từ 3 đến căn bậc hai của nó hay không. Nếu không chia hết cho bất kỳ số nào
trong khoảng này, thì số đó được coi là số nguyên tố và trả về true.
3. Trong hàm main, mã sử dụng các hàm trên để thực hiện các công việc sau:
− Tạo ba số nguyên tố ngẫu nhiên với 8 bit, 16 bit và 64 bit bằng cách gọi hàm
generateRandomPrime với các đối số tương ứng.
− Tìm 10 số nguyên tố lớn nhất dưới các số nguyên tố Mersenne đầu tiên bằng cách duyệt qua
danh sách mersennePrimes và giảm giá trị một đơn vị cho đến khi tìm được số nguyên tố lớn
nhất dưới nó.
Lab 3: RSA Public-Key Encryption
3
− Cho phép người dùng nhập một số nguyên tùy ý và kiểm tra xem số đó có phải là số nguyên tố
không bằng cách gọi hàm isPrime với số được nhập.
Output:
Code:
Lab 3: RSA Public-Key Encryption
4
Task 1.1.2:
Cách giải:
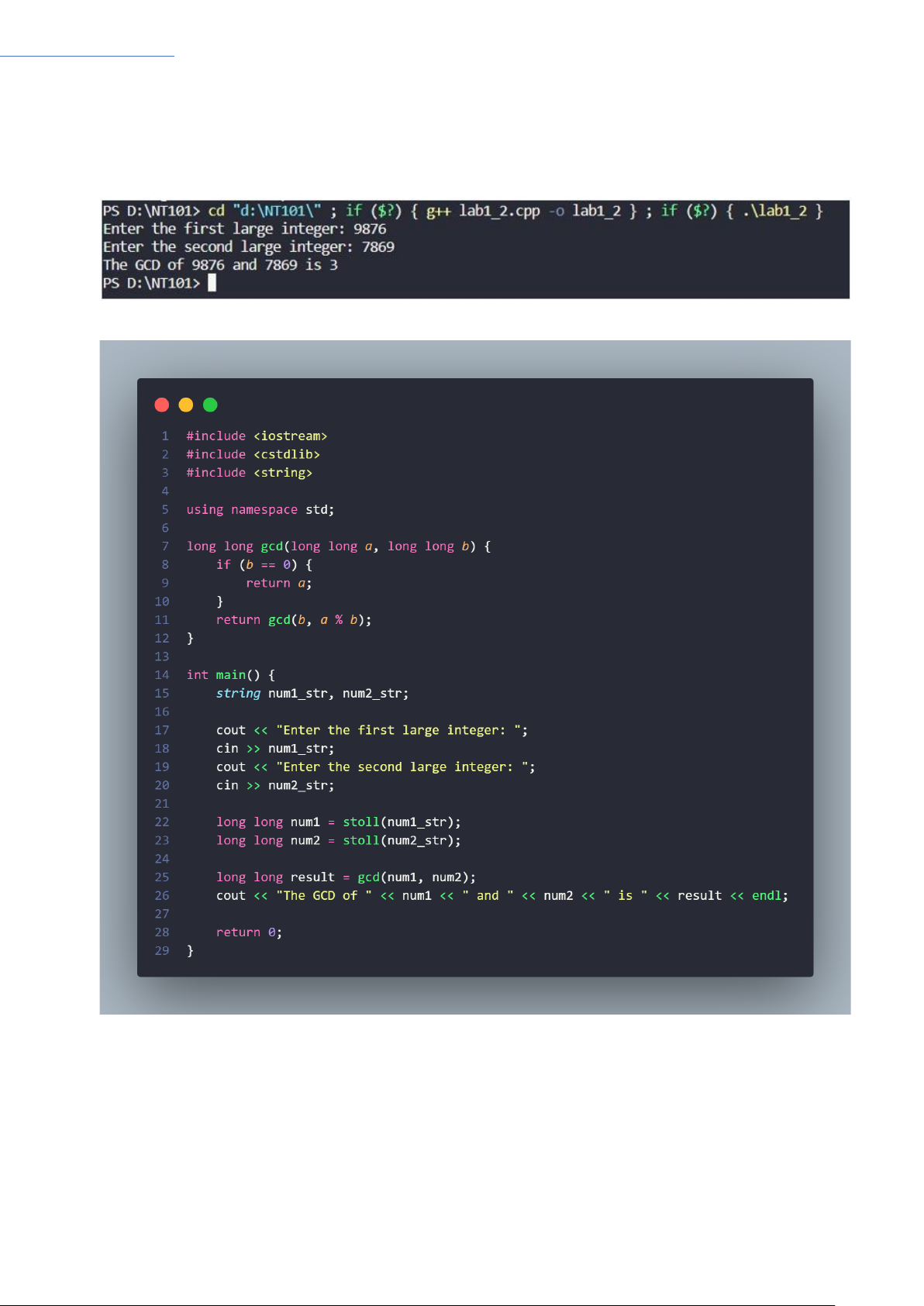
Chương trình C++ trên tính toán ước chung lớn nhất (GCD) của hai số nguyên lớn bằng cách sử
dụng thuật toán Euclidean. Đoạn mã thực hiện các bước sau:
− Người dùng nhập hai số nguyên lớn dưới dạng chuỗi.
Lab 3: RSA Public-Key Encryption
5
− Chuỗi đầu vào được chuyển thành số nguyên dạng long long.
− Hàm gcd(a, b) được sử dụng để tính GCD của hai số nguyên.
− Kết quả GCD được in ra màn hình.
Output:
Code:


























