Báo cáo hóa học: " Research Article Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method"

Chia sẻ: Nguyen Minh Thang | Ngày: | Loại File: PDF | Số trang:7

Thêm vào BST

Báo xấu

39
lượt xem 6
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tuyển tập báo cáo các nghiên cứu khoa học quốc tế ngành hóa học dành cho các bạn yêu hóa học tham khảo đề tài: Research Article Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Báo cáo hóa học: " Research Article Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method"

Hindawi Publishing Corporation EURASIP Journal on Wireless Communications and Networking Volume 2011, Article ID 983915, 7 pages doi:10.1155/2011/983915 Research Article Amplitude PDF Analysis of OFDM Signal Using Probabilistic PAPR Reduction Method Hyunseuk Yoo, Fr´ d´ ric Guilloud, and Ramesh Pyndiah ee Department of Signal and Communications, Telecom Bretagne, Technopole Brest Iroise, CS 83818, 29238 Brest cedex 3, France Correspondence should be addressed to Hyunseuk Yoo, hyunseuki@gmail.com Received 24 June 2010; Revised 2 December 2010; Accepted 19 January 2011 Academic Editor: Marc Moonen Copyright © 2011 Hyunseuk Yoo et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. To reduce the peak-to-average power ratio (PAPR) of an orthogonal frequency division multiplexing (OFDM) modulation scheme, one class of methods is to generate several OFDM symbols (candidates) carrying the same information and to select for transmission the one having the lowest PAPR. We derive a theoretical amplitude probability density function (PDF) of the selected OFDM symbol using order statistics. This amplitude PDF enables one to derive the signal-to-noise-plus-distortion ratio (SNDR) as a function of the number of candidates. Based on the SNDR derivation, theoretical error performance and statistical channel capacity are provided for this class of methods. The results match the simulations and make the system design easier. 1. Introduction The principle of probabilistic methods is to reduce the probability of high PAPR by generating several OFDM Orthogonal frequency division multiplexing (OFDM) is a symbols (multiple candidates) carrying the same informa- multicarrier multiplexing technique, where data is transmit- tion and by selecting the one having the lowest PAPR. ted through several parallel frequency subchannels at a lower The probabilistic method can also be classiﬁed into two rate. It has been popularly standardized in many wireless strategies: subblock partitioning strategy and entire block applications such as Digital Video Broadcasting (DVB), Dig- strategy. The subblock partitioning strategy, such as partial ital Audio Broadcasting (DAB), High Performance Wireless transmit sequence (PTS) [6–8], divides frequency domain Local Area Network (HIPERLAN), IEEE 802.11 (WiFi), and signals into several subblocks. On the other hand, the IEEE 802.16 (WiMAX). It has also been employed for wired entire block strategy, such as selected mapping (SLM) [8– applications as in the Asynchronous Digital Subscriber Line 10] and interleaving [11–13], considers the entire block for (ADSL) and power-line communications. generating multiple candidates. A signiﬁcant drawback of the OFDM-based system is its In this paper, we consider the entire block strategy of high Peak-to-Average Power Ratio (PAPR) at the transmitter, the probabilistic methods to generate multiple candidates. requiring the use of a highly linear ampliﬁer which leads to First, the probability density function (PDF) for the multiple low power eﬃciency [1]. Moreover, when an OFDM signal candidate system is analyzed. When the candidate having level works on the nonlinear area of ampliﬁer, the OFDM the lowest PAPR is selected, the PDF of the amplitude of a signals go through nonlinear distortions and degrade the selected OFDM symbol becomes the function of the number error performance. of candidates n. We apply the analyzed PDF (as a function of n) to Ochiai’s method [13] for obtaining the signal-to-noise- The various approaches to alleviate this problem in plus-distortion ratio (SNDR) as a function of n. Then, the OFDM-based systems can be classiﬁed into ﬁve categories: clip eﬀect transformation [2], coding [3], frame superposi- SNDR (as a function of n) can be used for analytical error performance. Note that in [13], the authors used the Rayleigh tion using reserved tones [4], expansible constellation point: PDF (single candidate) for obtaining the error performance tone injection [4] and active constellation extension [5], and of multiple candidate cases. However, we suggest using our probabilistic solutions [6–13].
2 EURASIP Journal on Wireless Communications and Networking PDF (multiple candidates) to obtain the theoretical error Throughout this paper, the following are also assumed: performance and also the statistical channel capacity for the according to the central limit theorem, the complex OFDM multiple candidate system. signal, which consists of a number of independent orthog- The paper is organized as follows: in Section 2, we onal subcarriers, is modeled as a complex Gaussian process describe the multiple candidate OFDM system, and analyze with Rayleigh envelope distribution. In addition, since the the PDF for the system. In Section 3, we derive the theoretical OFDM modulation is strictly band limited, we consider only performance, such as the SNDR (as a function of n), and in-band distortion. error rate, and also statistical channel capacity. In Section 4, an extension of the results to an oversampled SLM model, 2.2. PDF Analysis. Based on the assumption that the OFDM implementing the “clipping and ﬁltering” technique [14], is signal xi, j for i ∈ {1, . . . , n} and j ∈ {1, . . . , N } is tackled. Finally, we conclude this paper in Section 5. complex Gaussian distributed with mean 0 and variance 1, the envelope ri, j = |xi, j | is Rayleigh distributed with PDF fr 2. Multiple Candidate System given by ⎧ 2.1. Description. In this section, we describe the multiple ⎨2r · exp −r 2 , for r ≥ 0, candidate solution for reduction of PAPR. Figure 1 describes fr (r ) = ⎩ (3) the multiple candidate system and our PDF notation for for r < 0. 0, several variables. n candidates (frequency domain signal) are generated by the candidate generator, where this candidate According to the largest order statistics [15], the distribu- generator represents a class of probabilistic methods such as tion of the maximum of the amplitude values max j {ri, j } ∼ the SLM method [8–10] or the interleaving method [11– frmax is given by 13]. After the N -point Inverse Discrete Fourier Transform (IDFT), we get the n OFDM candidates (time domain N −1 r signal), xi = {xi,1 , xi,2 , . . . , xi,N }, i ∈ {1, . . . , n}. When we frmax (r ) = N fr (r ) fr (x)dx −∞ (4) deﬁne ri, j |xi, j |, then N −1 2 = N fr (r ) 1 − exp −r . |x1 | = r1 = r1,1 , r1,2 , . . . , r1,N −1 , r1,N , |x2 | = r2 = r2,1 , r2,2 , . . . , r2,N −1 , r2,N , When we select the candidate having a minimum peak amplitude among n candidates, according to the smallest . . order statistics [15], we obtain the PDF of the peak amplitude . . . . of the selected candidate mini [max j {|xi, j |}] ∼ frmax∗ (r ), (1) using frmax (r ): xi0 = ri0 = ri0 ,1 , ri0 ,2 , . . . , ri0 ,N −1 , ri0 ,N , . . n−1 ∞ . . . . frmax∗ (r ) = n · frmax (r ) · frmax (x)dx r (5) |xn | = rn = rn,1 , rn,2 , . . . , rn,N −1 , rn,N , N n−1 N −1 N = 2nNr S(r ) − S(r ) · 1 − S(r ) , and the peak detector selects the i0 th candidate, where i0 = argmini (max j {ri, j }) for i ∈ {1, . . . , n} and j ∈ {1, . . . , N }. ∞ N where r frmax (x)dx = 1 − (1 − exp(−r 2 )) and S(r ) = 1 − Then, the selected (i0 th) OFDM signal candidate is clipped exp(−r 2 ). by a nonlinear ampliﬁer, where we consider the soft clipping We now want to know the PDF of amplitude of the model [13] as follows: selected candidate ri0 ∼ fr ∗ . In (5), we have obtained frmax∗ (r ) ⎧ ⎪xi0 , j , for xi0 , j ≤ A, ⎪ from frmax (r ) using the smallest order statistics. Furthermore, ⎪ ⎨ since max j {ri0 , j } = mini [max j {ri, j }] ∼ frmax∗ (r ), we can also xi0 , j = g xi0 , j (2) ⎪A · xi0 , j , ⎪ express frmax∗ (r ) as a function of fr ∗ (r ) using the largest order for xi0 , j > A, ⎪ ⎩ x statistics. Then, i0 , j where A is the maximum permissible amplitude for the N −1 r frmax∗ (r ) = N · fr ∗ (r ) · fr ∗ (x)dx clipping model. 0 The clipped i0 th candidate is transmitted to the receiver (6) with its side information, where the side information N d Fr ∗ (r ) = contains the information of i0 and it is used for recovering the , dr original data. The side information protection depends on the various protection strategies, such as no side information r where Fr ∗ (r ) = 0 fr ∗ (x )dx . From (6), we can obtain method [9, 10] or coded side information method [12]. However, in this paper, for analyzing the pure eﬀect of 1/N r increasing n for the multiple candidate system, we assume Fr ∗ ( r ) = (7) frmax∗ (x)dx . that the side information is sent without errors. 0
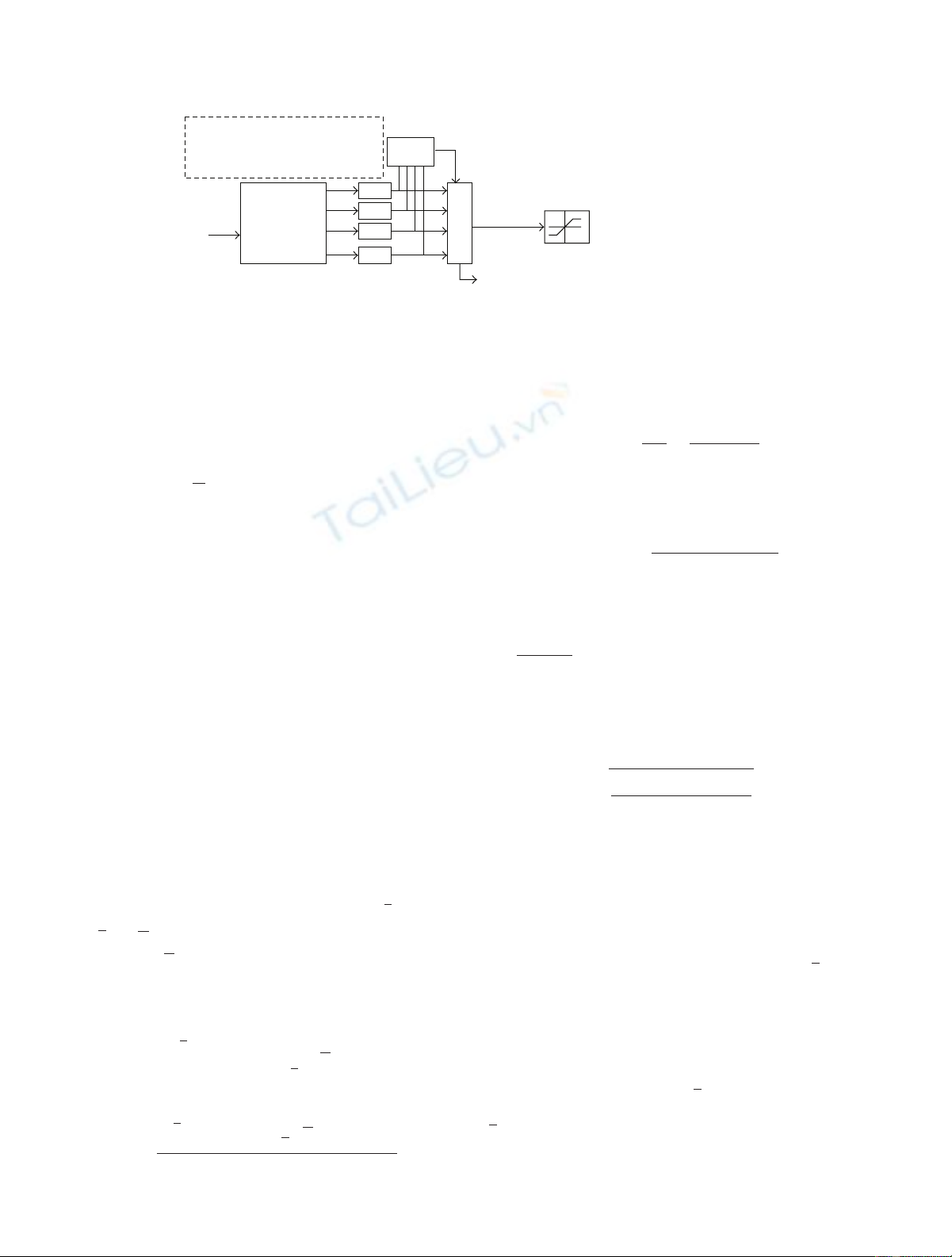
EURASIP Journal on Wireless Communications and Networking 3 xi = {xi,1 , · · · , xi,N } Peak i0 i0 = argi min{max j |xi, j |} |xi, j | ∼ fr detector x1 Soft max j {| xi, j |} ∼ frmax IDFT Original clipping x2 binary Multi candidate IDFT  mini [max j {|xi, j |}] Select data x3 generator IDFT ∼ frmax∗ + ... ... x∗ = xi0 xn modulation max j {|xi0, j |} IDFT |xi0 , j | ∼ fr ∗ Side information |xi, j |, and the peak detector selects the i0 th Figure 1: Multiple candidate system and its PDF notation for several variables. We deﬁne ri, j candidate, where i0 = argmini (max j {ri, j }) for i ∈ {1, . . . , n} and j ∈ {1, . . . , N }. Then, Kγn) , total attenuation factor, is the following: ( So, the PDF of the amplitude of the selected candidate is given by 2 (n α(n) Pin ) S (n) fr ∗ (r ) = Fr ∗ (r ) (11) Kγn) ( = (n) = . (n) Pout Pout 1/N −1 r 1 = · frmax∗ (r ) frmax∗ (x)dx Finally, SNDR(n) for the multiple candidate technique is N 0 (8) given by 1/N −1 Nn = n fr (r ) · 1 − 1 − S(r ) Kγn) Es /N0 ( SNDR(n) = . (12) N n−1 1 − Kγn) Es /N0 + 1 ( N −1 · S(r ) · 1 − S(r ) , where S(r ) = 1 − exp(−r 2 ). 3.2. Error Rate. Since we assume that the side informa- Figure 2 gives a comparison between the analytical and tion is transmitted without errors, the BER of QPSK- the simulation PDF in logarithm scale. Notice that the modulated signal over the AWGN channel is given by PB = analytical line ﬁts the simulation points. Q( SNDR(n) ). Furthermore, QPSK symbol error rates (SER) are as follows: PS = 1 − (1 − PB )2 . 3. Theoretical Performance For the frequency-nonselective slowly (constant attenu- ation during one OFDM symbol) Rayleigh-fading channel 3.1. SNDR(n) for Multiple Candidate System. Now, we apply [16], the BER is given by (8) to obtaining the signal-to-noise-plus-distortion ratio ⎛ ⎞ (SNDR) as a function of n, by using Ochiai’s method [13]. κ2 Kγn) Es /N0 ( ∞ ⎜ ⎟ The authors in [13] used the Rayleigh PDF, fr , to obtain the PB = Q⎝ ⎠ fr (κ)dκ, (13) SNDR of a multiple candidate system. However, as shown 1 − Kγn) ( κ2 Es /N0 + 1 0 in Figure 2, the PDF of amplitude of the selected candidate is not Rayleigh PDF anymore, being the function of n. where κ is the channel attenuation which is Rayleigh Therefore, we use the PDF of (8), fr ∗ , to obtain the SNDR of distributed with E[κ2 ] = 1. multiple candidate system, and hereafter we will use SNDR(n) Figure 3 shows the error performance comparison over as a function of n, instead of SNDR. AWGN channel and frequency-nonselective slowly fading For that, the PAPR threshold for clipping λ is deﬁned channel, where the analytical approach and the simulation (n) 2 ∞ (n (n (A ) /Pin ) , where the input power Pin ) = 0 r 2 · results are compared. For the simulations, 1024-point FFT as λ pairs are considered and the signals are modulated by QPSK. (n) fr ∗ (r )dr and A is the maximum permissible amplitude for At the transmitter, the OFDM signals are clipped at λ = 0 dB. the multiple candidate system. In the ﬁgure, we can see that the simulated SER is well Then, based on fr ∗ in (8), the total output power for the matched on the analytical line, and an error ﬂoor appears at multiple candidate solution after clipping is obtained as large SNR because of the clipping noise. In addition, we can see better error performance, when n increases. (n) ∞ A (n) 2 (n) (9) r 2 fr ∗ (r )dr + Pout = A fr ∗ (r )dr , Since our theoretical analysis matches well the simula- (n) A 0 tions, we can estimate the analytical frame error ﬂoor as a and the signal distortion rate, α(n) , is given by function of the PAPR threshold λ (see Figure 4). We can see that the error ﬂoor level can decrease, by increasing n and/or (n) ∞ (n) A r 2 fr ∗ (r )dr + λ. Our analytical approach makes it possible to foresee the A r fr ∗ (r )dr (n) 0 A (10) (n) = expected level of the error rate without a time-consuming α . (n Pin ) simulation.
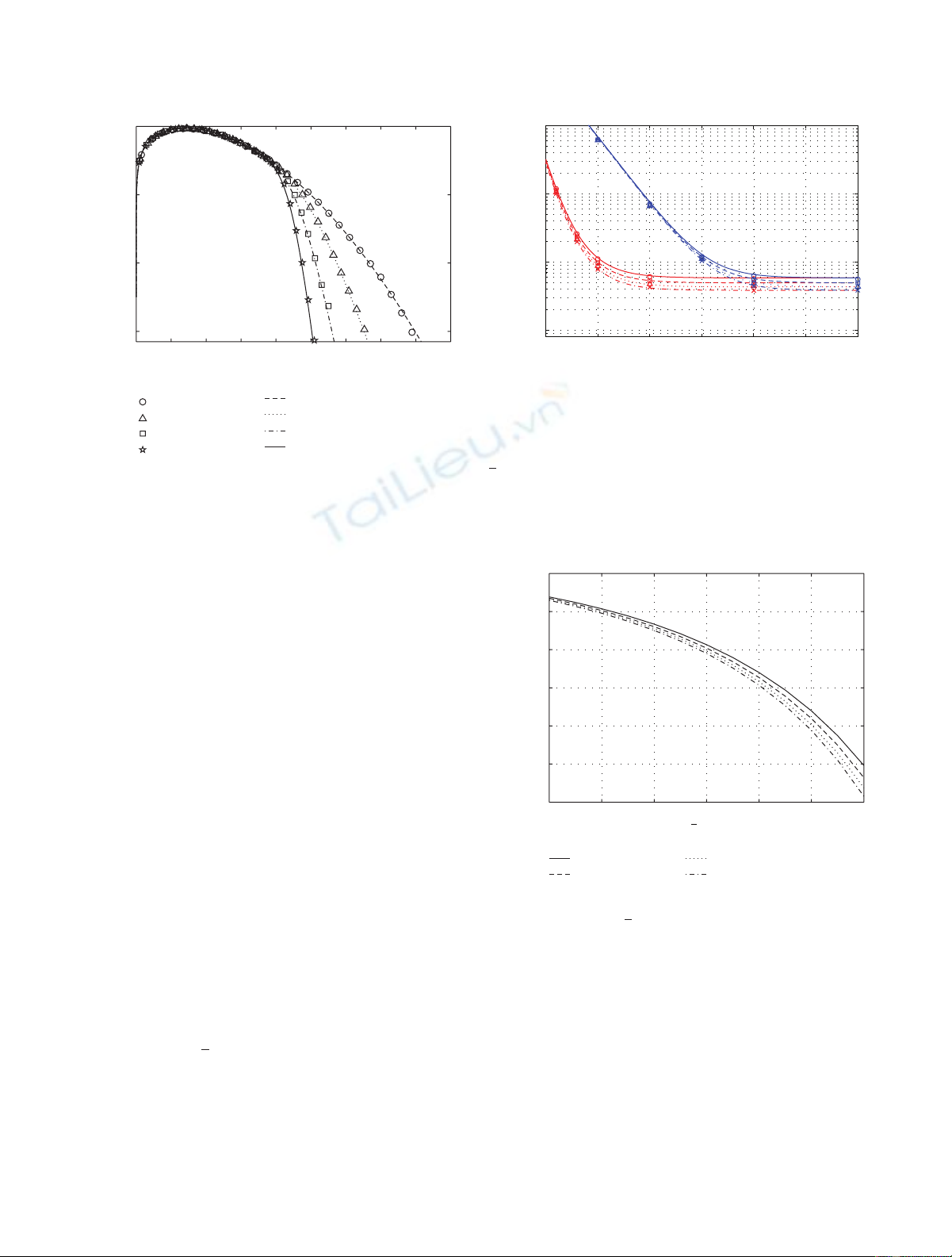
4 EURASIP Journal on Wireless Communications and Networking 10−2 100 fr ∗ in logarithmic domain 10−3 10−2 SER 10−4 10−4 10−5 10−6 10 20 30 40 50 60 70 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 Eb /N0 (dB) Amplitude, |x| Figure 3: Symbol Error Rate (SER) comparison between the n = 1, analytical n = 1, simulated analytical approach (line) and the simulation results (marker) over n = 2, analytical n = 2, simulated AWGN channel (red) and frequency-nonselective slowly fading n = 4, analytical n = 4, simulated channel (blue), where the data is QPSK modulated, and 1024- n = 8, analytical n = 8, simulated point FFT pairs are considered. The OFDM symbols are clipped at λ = 0 dB. In the ﬁgure, the lines represent our analytical approach, Figure 2: Analytical and simulated logarithmic PDF for fr ∗ (x) such as solid line (n = 1), dash line (n = 2), dot line (n = 4), and corresponding to N = 128. dash-dot line (n = 8). The markers represent the simulation results, such as ◦ (n = 1), (n = 2), (n = 4), × (n = 8). 3.3. Channel Capacity. We consider the channel capacity of 100 selected and clipped OFDM symbols for a multiple candidate system. For this, we take into consideration the M-ary 10−2 Input AWGN channel models [17]. Suppose that the receiver Analytical frame error ﬂoor knows the exact information about which candidate has 10−4 been transmitted. Then, the channel capacity of transmitted symbols is CM-ary = h(yi0 ) − h(yi0 | xi0 ), where yi0 is the received symbol, and from which we may write 10−6 +∞ 10−8 CM-ary = − p(I , Q)log2 p(I , Q)dI dQ −∞ (14) 10−10 − log2 2πeσ 2 , 10−12 where p(I , Q) is the two-dimensional PDF of received 0 0.5 1 1.5 2 2.5 3 symbol with the Gaussian noise variance σ 2 = 0.5/ SNDR(n) λ (dB) in each dimension. N = 1024, n = 1 N = 1024, n = 4 Figure 5 illustrates the channel capacity for 16-QAM case N = 1024, n = 8 N = 1024, n = 2 (up) and 64-QAM case (down) over M-ary Input AWGN channel. The ﬁgure implies that, due to the clipped symbol, Figure 4: Analytical Frame Error Rate at the error ﬂoor level for it is impossible to achieve error-free performance. However, the clipping threshold λ. In the case, N = 1024 and the QPSK as the number of candidate increases, we can obtain modulation is considered. theoretical capacity gains as long as SNDR(n) increases. In particular, the channel symbols of M-QAM, where M 16, are so sensitive to the clipping noise that the multiple with a large N is usually assumed to have a Gaussian PDF candidate system can attain additional channel capacity gains eﬀectively. When SNR = 45 dB, the measured capacity gain in the real and imaginary parts. However, for the multiple candidate system, this Gaussian assumption no longer holds. is 0.1284 bits/channel symbol with 16 candidates (64-QAM symbols clipped at λ = 2 dB). In this section, we show mathematical non-Gaussian PDF for the multiple candidate system. 4. Application: Oversampling and Filtering 4.1. Presentation of Extended Model. The multiple candidate We present an extension of the multiple candidate system: system in the presence of the soft limiter can be extended to combination with an oversampling and ﬁltering technique the oversampling and ﬁltering technique [14]. In this case, n frequency domain OFDM symbols Xi = {Xi,1 , . . . 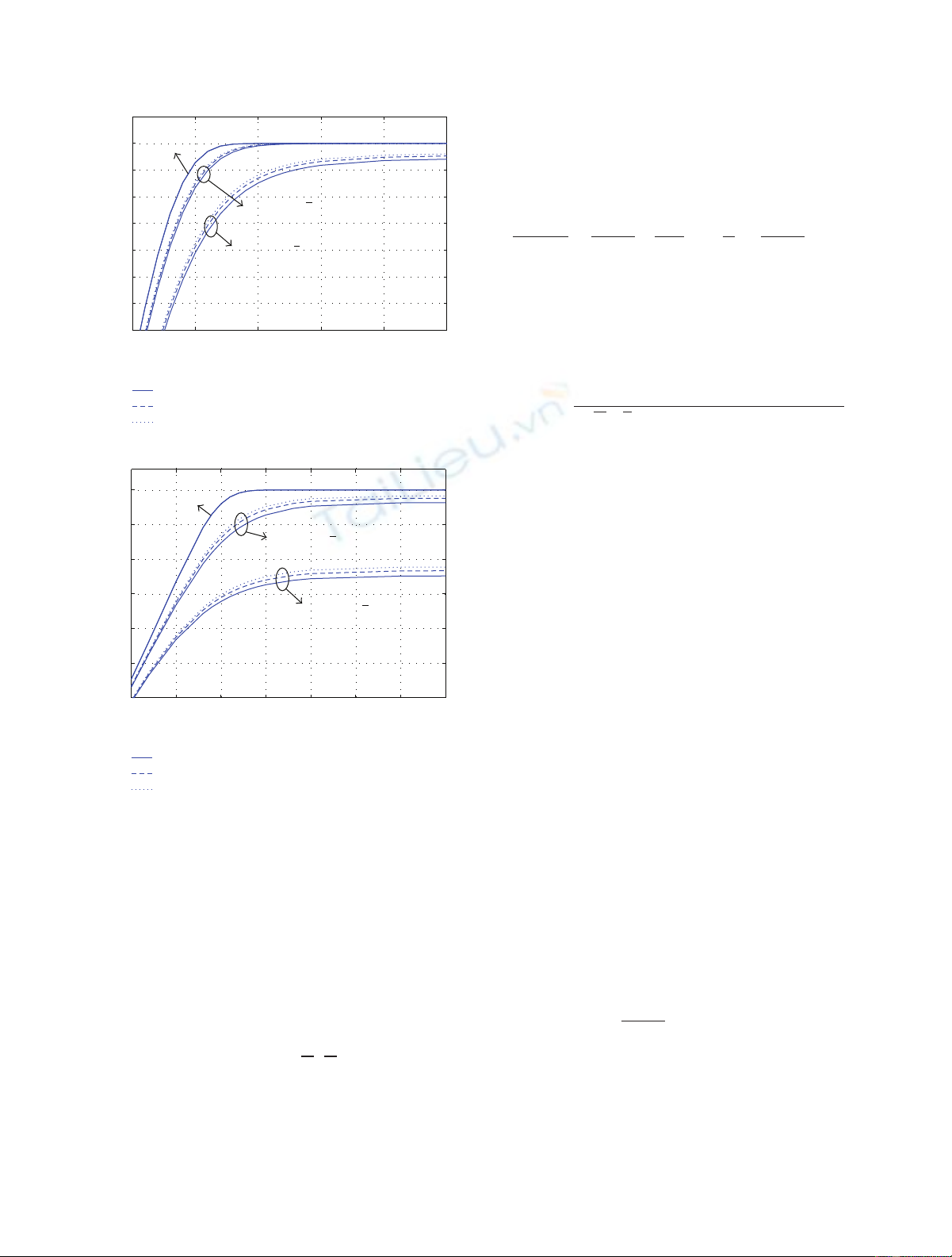, Xi,N } [14]. For the single-candidate system, an OFDM symbol
EURASIP Journal on Wireless Communications and Networking 5 yielding a ﬁltered signal xi0 = {xi0 ,1 , . . . , xi0 ,N } which will be converted into an analog signal xi0 (t ). Unclipped 4 Capacity (bits/channel symbol) Let SNDR(n) be the SNDR of the kth subcarrier for n k 3.9 candidate system, then its inverse can be expressed as [14] 3.8 ⎛ ⎞ Clipped at λ = 4 dB N −1 3.7 1 1 1⎝ 1 1⎠ (n) = (n) + SNR 1 + N (n) , (16) SNDRk SDRk k=0 SDRk Clipped at λ = 2 dB 3.6 3.5 where SNR denotes the signal-to-noise ratio for the channel, 3.4 and SDR(n) denotes the signal-to-distortion ratio of the kth k subcarrier for n candidate system. 3.3 10 15 20 25 30 35 In (16), SDR(n) can be expressed as [14] k SNR (dB) n=1 Kγn) ( SDR(n) = √ √ n=4 , k (n) (n) − Kγ N/ L DFT L, Rxi0 [m]/Pout n = 16 k (17) (a) (n) where Pout is given in (9) and Rxi0 [m] is the autocorrelation 6 Unclipped function of the clipped signal. Capacity (bits/channel symbol) Let xi0 ,k a1 + jb1 and xi0 ,k+m a2 + jb2 , then the clipped 5.5 Clipped at λ = 4 dB signals are given by xi0 ,k g (a1 + jb1 ) and xi0 ,k+m g (a2 + 5 jb2 ), and the autocorrelation function Rxi0 [m] is given by 4.5 Rxi0 [m] = R E xi∗,k · xi0 ,k+m Clipped at λ = 2 dB 0 4 = E g ∗ a1 + jb1 g a2 + jb2 (18) 3.5 g ∗ a1 + jb1 g a2 + jb2 = D(a1 ,b1 ,a2 ,b2 ) 3 10 15 20 25 30 35 40 45 · f (a1 , a2 , b1 , b2 )da1 db1 da2 db2 , SNR (dB) n=1 where E[·] denotes the expectation operation. n=4 n = 16 4.2. Inaccuracy of Gaussian Assumption. For the single can- (b) didate case, since {a1 , a2 , b1 , b2 } are assumed to be Gaussian distributed, f (a1 , a2 , b1 , b2 ) is expressed as a joint Gaussian Figure 5: Channel capacity for 16-QAM case (a) and 64-QAM case PDF [14, 18]. However, for the multiple candidate case (b), where N = 1024 and M-ary Input AWGN channel (MI-AWGN) (n > 1), since the amplitude of the selected candidate is not is considered. Rayleigh distributed, such as (8), this Gaussian assumption no longer holds. In the rest of this paper, we consider the PDF of {a1 , b1 , a2 , b2 } ∼ fa for the multiple candidate case. are zero-padded, and L-times oversampled IDFT processes Without loss of generality, we consider a = a1 and b = b1 , are performed, generating n candidates xi = {xi,1 , . . . , xi,LN } where a and b are assumed to be independent and identically in the time domain, where the L-times oversampled IDFT distributed. Then, the amplitude is deﬁned as operation is denoted as ⎛ ⎧ ⎫⎞ ⎪ ⎪ ⎪ ⎪ ⎨ ⎬⎟ a2 + b2 ∼ fh (r ) = fr ∗ (r ), ⎜ (19) h ⎜L, Xi , 0, . . . , 0 ⎟. xi = IDFT⎝ ⎪ (15) ⎪⎠ ⎪ ⎪ ⎩ ⎭ (L−1)N where fr ∗ (r ) is given by (8). h2 ≥ 0, its characteristic Deﬁning a power variable y Then, the candidate xi0 = {xi0 ,1 , . . . , xi0 ,LN } with the function [15] is given by minimum PAPR is selected, and clipped by the soft limiter, where |xi0 ,k | ∼ fr ∗ , k ∈ {1, . . . , LN }, as in (8). The clipped ∞ signal xi0 = {xi0 ,1 , . . . , xi0 ,LN } goes through a band pass ﬁlter exp j ωr 2 fh (r )dr , ϕ y (ω) = (20) (BPS) which removes out-of-band frequency components, 0
6 EURASIP Journal on Wireless Communications and Networking Our analytical approach to obtaining the SNDR(n) and let y1 a2 and y2 b2 , such that y = y1 + y2 . Since y1 and y2 are independent and have an identical PDF f y1 = f y2 , implies that the estimation of error rate is achievable without we get time-consuming simulation, making system level design easier. Note that the error ﬂoor level is usually decreased 2 by implementing channel coding techniques. In our future ϕ y (ω) = ϕ y1 (ω) · ϕ y2 (ω) = ϕ y1 (ω) work, we will take channel coding into account for error (21) 1/ 2 performance analysis. ∴ ϕ y 1 (ω ) = ϕ y (ω ) . References Then, f y1 (r ) = f y2 (r ) is given by [1] H. Sari, A. Svensson, and L. Vandendorpe, “Multicarrier f y 1 (r ) = f y 2 (r ) systems,” EURASIP Journal on Wireless Communications and (22) +∞ Networking, vol. 2008, Article ID 598270, 2008. 1 1/ 2 = exp − jωr dω. ϕ y (ω) [2] H. Saeedi, M. Sharif, and F. Marvasti, “Clipping noise 2π −∞ cancellation in OFDM systems using oversampled signal Now, we consider the case a ≥ 0 with the PDF of fa (r ). reconstruction,” IEEE Communications Letters, vol. 6, no. 2, pp. 73–75, 2002. Notice that a negative value of a will have its symmetrical [3] A. E. Jones and T. A. Wilkinson, “Combined coding for error PDF. The characteristic function of y1 = a2 is given by control and increased robustness to system nonlinearities in ∞ OFDM,” in Proceedings of the 46th IEEE Vehicular Technology exp j ωr 2 fa (r )dr ϕ y 1 (ω ) = Conference (VTC ’96), pp. 904–908, Atlanta, Ga, USA, May 0 1996. ∞ [4] J. Tellado and J. Cioﬃ, “Peak power reduction for multicarrier (23) f a (r ) = exp j ωy1 · · d y1 . transmission,” in Proceedings of the IEEE Communications 2r 0 Theory Mini-Conference (CTMC ’98), IEEE Global Communi- = f y1 ( y1 )= f y1 (r 2 ) cations Conference (GLOBECOM ’98), Sydney, Australia, 1998. [5] B. S. Krongold and D. L. Jones, “PAR reduction in OFDM Finally, by using (22) and (23), we get via active constellation extension,” IEEE Transactions on Broadcasting, vol. 49, no. 3, pp. 258–268, 2003. fa (r ) = 2r f y1 r 2 [6] Y. Xiao, X. Lei, Q. Wen, and S. Li, “A class of low complexity (24) +∞ PTS techniques for PAPR reduction in OFDM systems,” IEEE r 1/ 2 exp − jωr 2 dω, = ϕ y (ω ) Signal Processing Letters, vol. 14, no. 10, pp. 680–683, 2007. π −∞ [7] C. Siegl and R. F. H. Fischer, “Partial transmit sequences which denotes the mathematical non-Gaussian PDF of a = for peak-to-average power ratio reduction in multiantenna R{xi0 ,k } or b = I{xi0 ,k }. OFDM,” EURASIP Journal on Wireless Communications and Networking, vol. 2008, Article ID 325829, 2008. [8] S. H. Muller and J. B. Huber, “Comparison of peak power 5. Conclusion reduction schemes for OFDM,” in Proceedings of the IEEE Global Communications Conference (GLOBECOM ’97), pp. 1– We study the probability density function (PDF) analysis 5, November 1997. and the signal-to-noise-plus-distortion ratio (SNDR) of [9] R. W. B¨ uml, R. F. H. Fischer, and J. B. Huber, “Reducing a a multiple candidate system for reducing the PAPR in the peak-to-average power ratio of multicarrier modulation OFDM modulation system. Since the selected OFDM symbol by selected mapping,” Electronics Letters, vol. 32, no. 22, pp. (candidate) has an amplitude PDF which is function of the 2056–2057, 1996. number of candidates n, the derived SNDR(n) is also the [10] B. K. Knoo, S. Y. Le Goﬀ, C. C. Tsimenidis, and B. S. Sharif, function of n, and it can be used for estimation of theoretical “OFDM PAPR reduction using selected mapping without side information,” in Proceedings of the IEEE International error performance and statistical channel capacity. Conference on Communications (ICC ’07), pp. 4341–4345, June In this paper, the side information is assumed not to be erroneous for analyzing the pure eﬀect of multiple 2007. [11] A. D. S. Jayalath and C. Tellambura, “Reducing the peak-to- candidates. The analytical estimation matches well the average power ratio of orthogonal frequency division multi- simulation results, and with this study, we conclude that the plexing signal through bit or symbol interleaving,” Electronics more the candidates, not only the better PAPR reduction Letters, vol. 36, no. 13, pp. 1161–1163, 2000. performance, but also the better error performance and the [12] A. D. S. Jayalath and C. Tellambura, “Peak-to-average power more gain of channel capacity, under the assumption of side ratio reduction of an OFDM signal using data permutation information transmission without error, and at the expense with embedded side information,” in Proceedings of the IEEE of computational complexity for n IFFT circuits. International Symposium on Circuits and Systems (ISCAS’ 01), Furthermore, the amplitude PDF analysis enables one to pp. 562–565, April 2000. apply to a probabilistic PAPR reduction system jointly with [13] H. Ochiai and H. Imai, “Performance of the deliberate “oversampling and ﬁltering” technique. In this application, clipping with adaptive symbol selection for strictly band- since the selected candidate is not complex Gaussian dis- limited OFDM systems,” IEEE Journal on Selected Areas in tributed, more investigation for SNDR is required. Communications, vol. 18, no. 11, pp. 2270–2277, 2000.
EURASIP Journal on Wireless Communications and Networking 7 [14] H. Ochiai and H. Imai, “Performance analysis of deliberately clipped OFDM signals,” IEEE Transactions on Communica- tions, vol. 50, no. 1, pp. 89–101, 2002. [15] A. Papoulis and S. U. Pillai, Probability, Random Variables and Stochastic Processes, McGraw-Hill, New York, NY, USA, 4th edition, 2002. [16] J. G. Proakis, Digital Communications, McGraw-Hill, New York, NY, USA, 4th edition, 2001. [17] W. E. Ryan and S. Lin, Channel Codes Classical and Modern, Cambridge University Press, Cambridge, UK, 2009. [18] P. Banelli and S. Cacopardi, “Theoretical analysis and perfor- mance of OFDM signals in nonlinear AWGN channels,” IEEE Transactions on Communications, vol. 48, no. 3, pp. 430–441, 2000.