
Chapter 3
Flow - stability

Introduction
• focus on stability of loose non-cohesive grains
• rock: important material for protection
• grains may vary in size from μc (sand) to m (rock)
Uniform flow – Horizontal bed
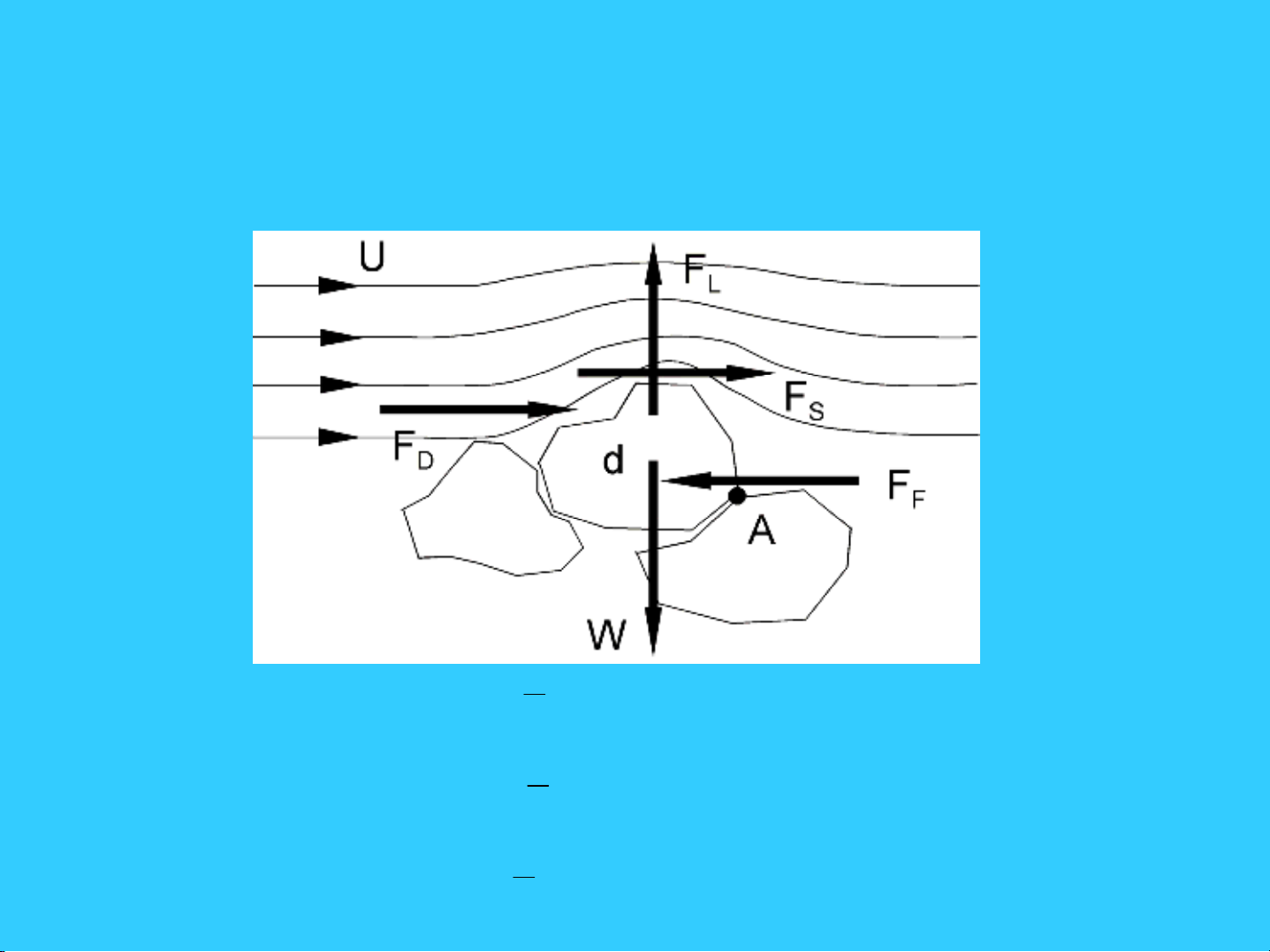
Forces on a grain in flow
1
2
1
2
1
2
2
DD
Dw
222
SS
Fww
2
LL
Lw
Drag force : =
Cu
FA
Shear force : = F
Cu ud
FA
Lift force : =
Cu
FA
ρ
ρρ
ρ
⎫
⎪
⎪
⎪≈
⎬
⎪
⎪
⎪
⎭

Balance equations
d g K =
u
d g = d g
-
u2
c
w
ws
2
cΔ→Δ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
∝
ρ
ρρ
d
g ) - (
d
u
dO W = dO
F
: 0 = M
W =
F
: 0 = V
FW x f =
F
: 0 = H
3
ws
22
c
w
SD,
L
F
SD,
ρρρ
∝
⎪
⎭
⎪
⎬
⎫
⋅⋅Σ
Σ
=Σ
)()(
Relation between load and strength
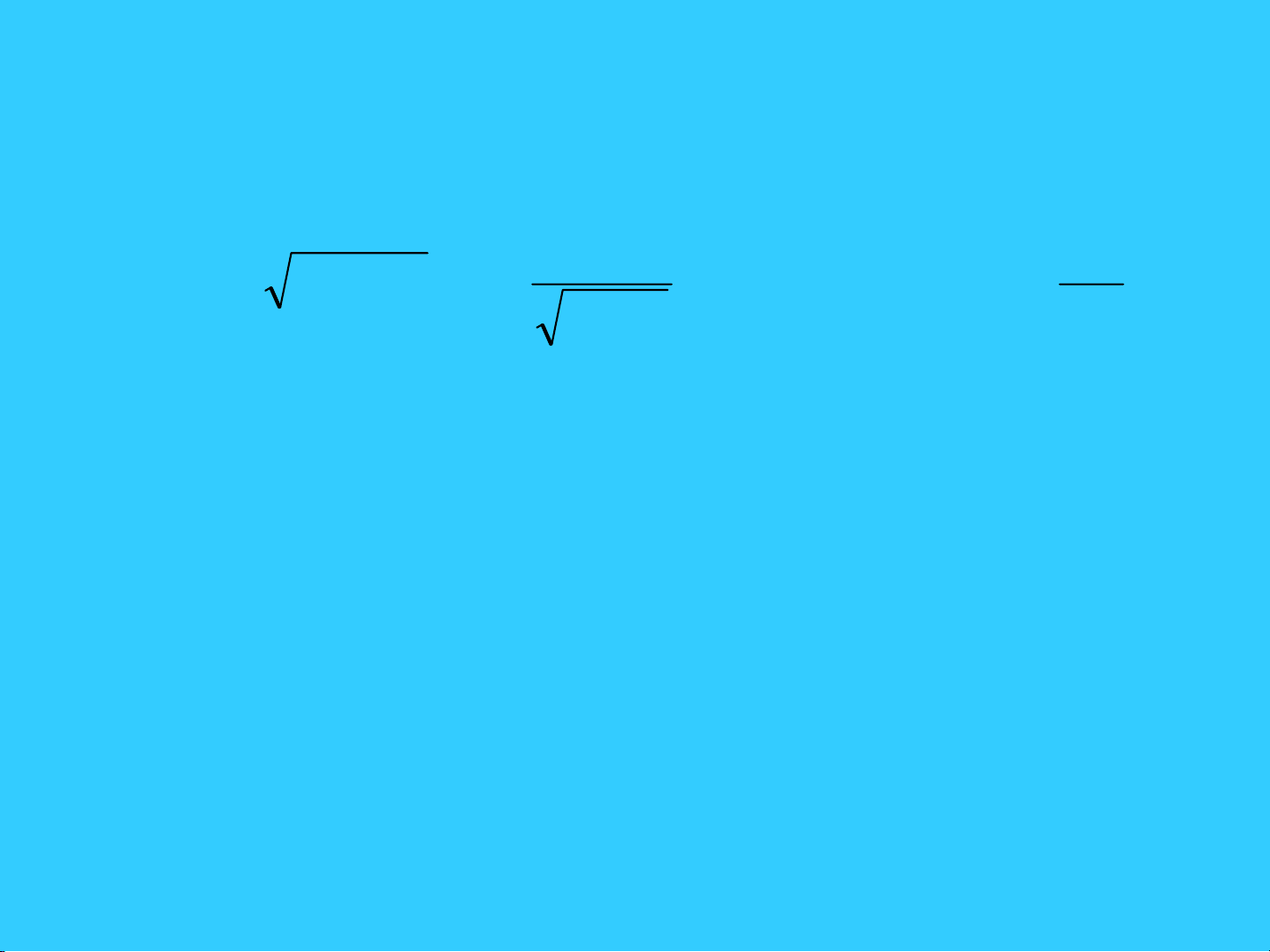
Isbash (1930)
g 2
u
0.7 = d or 1.7 =
d g
u
or d g 2 1.2 =
u
2
cc
cΔ
Δ
Δ
used for first approximation when:
• relation between velocity and waterdepth not clear
(e.g a jet entering a body of water)


























