BỘ CÂU HỎI MINH HỌA
ĐỀ THI ĐÁNH GIÁ TƯ DUY LĨNH VỰC TƯ DUY MÔN TOÁN
Câu 1 (M1): Bạn Hải lấy một cặp số tự nhiên phân biệt rồi tính số dư khi chia tổng lập
phương của hai số cho tổng các chữ số của số lớn trong hai số đó. Nếu làm theo đúng quy
tắc của bạn Hải với cặp số (31; 175) ta thu được kết quả bằng
A. 2
B. 5
C. 0
D. 3
Đáp án: D
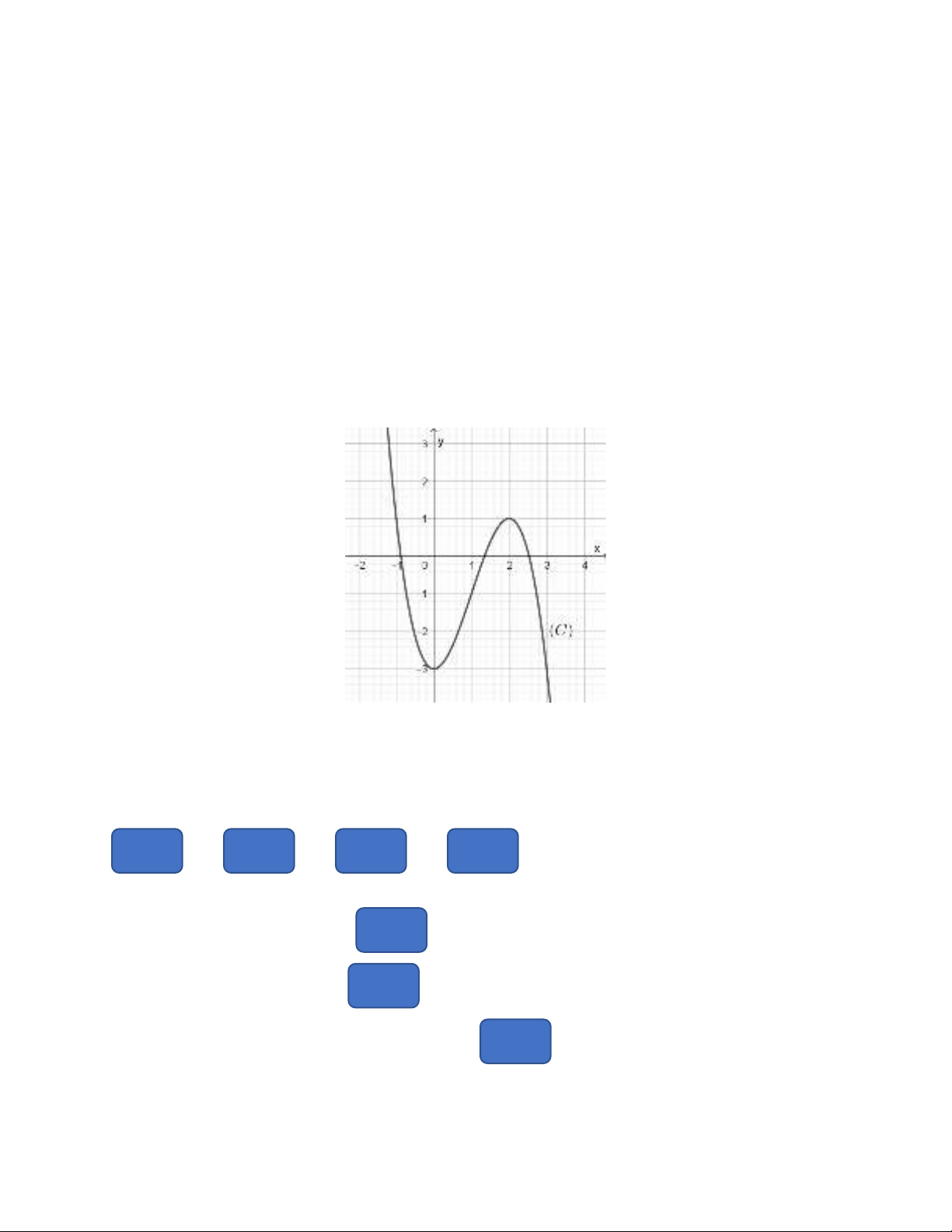
Câu 2 (M1): Cho hàm số bậc ba có đồ thị
( )
C
như hình vẽ sau.
Kéo ô thích hợp thả vào vị trí tương ứng để hoàn thành các câu sau:
Số điểm cực trị của hàm số là [vị trí thả 1].
Giá trị cực đại của hàm số là [vị trí thả 2].
Số giao điểm của đồ thị
( )
C
và trục hoành là [vị trí thả 3].
Đáp án:
Số điểm cực trị của hàm số là .
Giá trị cực đại của hàm số là .
Số giao điểm của đồ thị
( )
C
và trục hoành là .
3
2
4
1
2
1
3
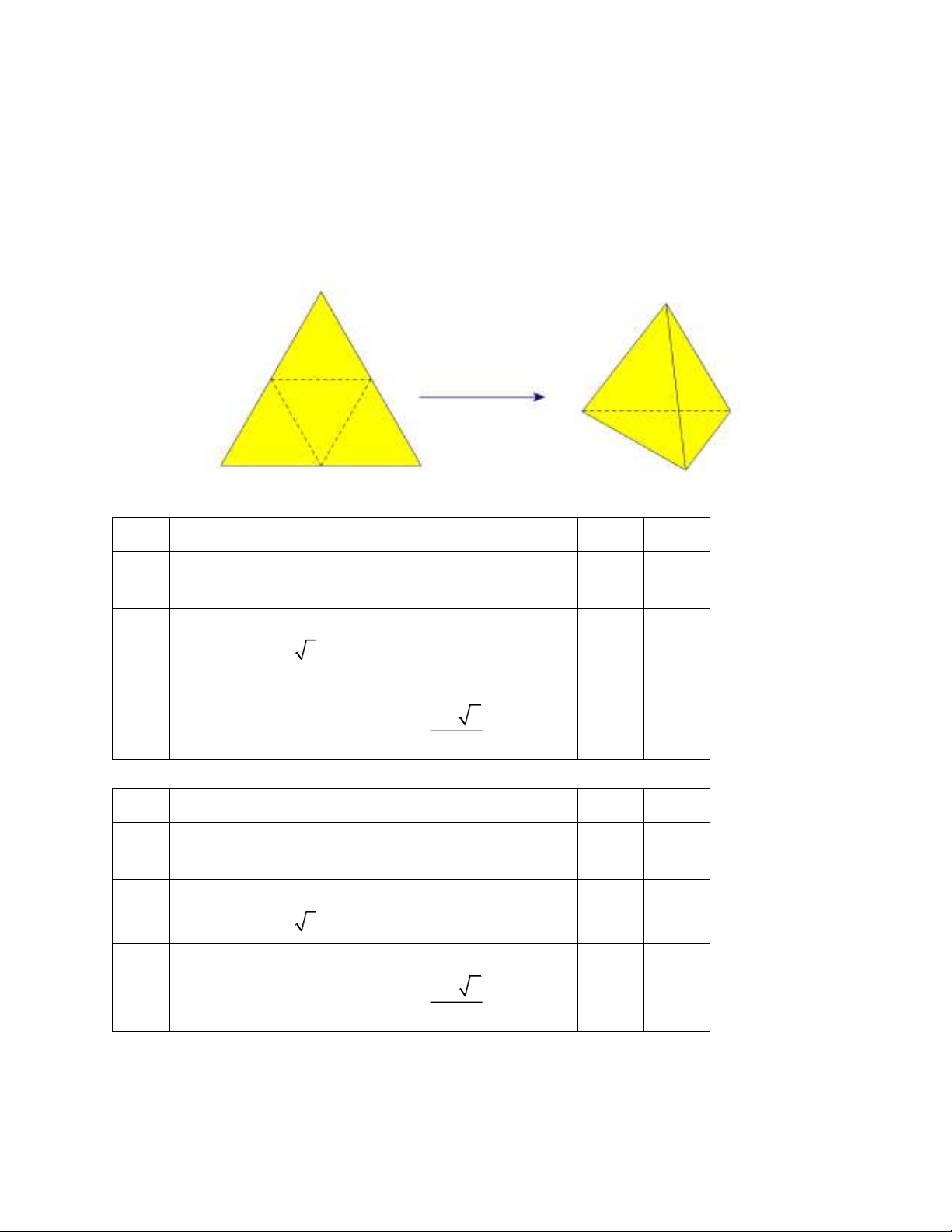
Câu 3 (M2): Trong tiết học về hình đa diện đều, cô giáo Hạnh hướng dẫn học sinh tạo ra
hình tứ diện đều như sau:
Đầu tiên, cô giáo lấy một miếng bìa hình tam giác đều có cạnh dài 10 cm. Tiếp đó, gấp
miếng bìa theo các đường kẻ nối trung điểm giữa các cạnh của miếng bìa (tham khảo hình
vẽ). Sau đó, cô giáo dán các mép lại, chúng ta sẽ có một hình tứ diện đều (giả sử phần bìa
tại các mép dán không đáng kể).
Mỗi phát biểu sau là đúng hay sai?
STT
Phát biểu
Đúng
Sai
1
Độ dài cạnh của hình tứ diện đều được tạo ra
bằng 10 cm.
2
Diện tích toàn phần của hình tứ diện đều được
tạo ra bằng
3
Thể tích của khối tứ diện đều được tạo thành bởi
hình tứ diện đều nói trên bằng
3
125 2 .
12 cm
Đáp án:
STT
Phát biểu
Đúng
Sai
1
Độ dài cạnh của hình tứ diện đều được tạo ra
bằng 10 cm.
X
2
Diện tích toàn phần của hình tứ diện đều được
tạo ra bằng
X
3
Thể tích của khối tứ diện đều được tạo thành bởi
hình tứ diện đều nói trên bằng
3
125 2 .
12 cm
X
Câu 4 (M2): Cho hàm số
( )
3
logf x x x=+
và biểu thức
( ) ( ) ( )
1P xf x f x f

= − −
.
Kéo ô thích hợp thả vào vị trí tương ứng để hoàn thành các câu sau:
Giá trị của biểu thức P tại
1
27
x=
bằng [vị trí thả 1].
Số nghiệm nguyên thuộc đoạn
1;5
của bất phương trình
1P−
là [vị trí thả 2].
Số nghiệm thực của phương trình
2P=−
là [vị trí thả 3].
Đáp án:
Giá trị của biểu thức P tại
1
27
x=
bằng .
Số nghiệm nguyên thuộc đoạn
1;5
của bất phương trình
1P−
là .
Số nghiệm thực của phương trình
2P=−
là .
Câu 5 (M2): Một người dùng khi đăng nhập vào một trang web sẽ được cấp một mã kiểm
tra là một dãy số gồm 5 chữ số. Giả sử mỗi chữ số trong mã được hệ thống tạo mã chọn
ngẫu nhiên trong phạm vi từ 0 tới 9, xác suất để một mã kiểm tra tạo ra có ít nhất hai chữ
số 0 là (Các kết quả làm tròn đến chữ số thập phân thứ tư).
A. 0,0729
B. 0,0815
C. 0,9185
D. 0,1000
Đáp án: B
Câu 6 (M2): Xét những tờ giấy hình chữ nhật, kẻ ca-rô cỡ 𝑚 × 𝑛 ô vuông, một cách phân
chia “tốt” được xác định khi ta chỉ dùng những dòng kẻ có sẵn chia tờ giấy thành những
phần bằng nhau sao cho mỗi phần đều là hình vuông cỡ 𝑝 × 𝑝 ô.
Chẳng hạn, ở hình dưới, bằng những dòng kẻ được tô màu xanh, ta xác định một cách phân
chia “tốt” với m = 9, n = 12, p = 3.
1
4
2
3
2
4
1
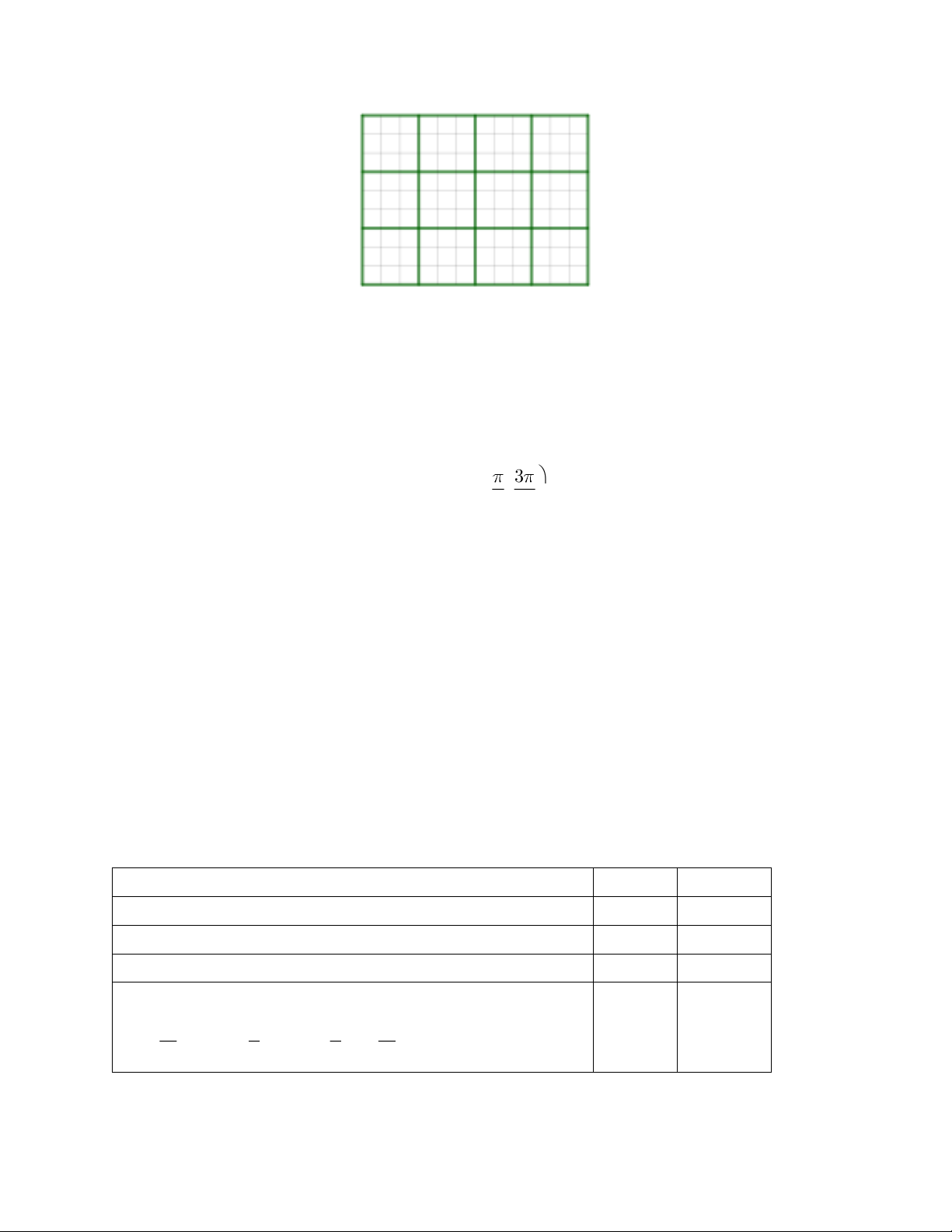
Số cách phân chia “tốt” đối với một tờ giấy ca-rô cỡ 120 ×300 là
A. 12 cách.
B. 60 cách.
C. 30 cách.
D. 36000 cách.
Đáp án: A
Câu 7 (M2): Tổng tất cả các nghiệm thuộc
−

3
;
22
của phương trình
xx+=sin cos2 0
bằng …….. (kết quả làm tròn đến chữ số thập phân thứ hai, biết π ≈ 3,14).
Đáp án: 4,71
Câu 8 (M2): Biết rằng giá trị nhỏ nhất của hàm số
( )
32
3f x x x m
= − − +
trên đoạn
1;1
−
bằng 1 thì giá trị của tham số m thuộc những khoảng nào trong các khoảng dưới đây?
A. (0; 4)
B. (1; 5)
C. (2; 6)
D. (3; 7)
Đáp án: C, D
Câu 9 (M3): Trong không gian Oxyz, cho hình chóp đều S.ABCD có
( ) ( ) ( )
3;2;1 , 1;2;0 , 3;0;0S A C
. Gọi E là trung điểm của BD. Gọi I là tâm mặt cầu (S) ngoại
tiếp của hình chóp S.ABCD. Mỗi phát biểu sau là đúng hay sai?
Phát biểu
Đúng
Sai
I cách đều ba điểm S, A, C.
I thuộc đường thẳng SE.
I cách đều mặt đáy và mặt bên của hình chóp.
Phương trình mặt cầu (S) là
2 2 2
11 5 5 11
6 6 6 4
x y z
− + − + − =
.
Đáp án:
Phát biểu
Đúng
Sai
I cách đều ba điểm S, A, C.
X
I thuộc đường thẳng SE.
X
I cách đều mặt đáy và mặt bên của hình chóp.
X
Phương trình mặt cầu (S) là
2 2 2
11 5 5 11
6 6 6 4
x y z
− + − + − =
.
X
Câu 10 (M3): Xưởng gỗ Bách Mộc thiết kế một mẫu đồ chơi gồm một khối nón và
một khối trụ có cùng bán kính đáy chồng lên nhau (như hình vẽ). Biết chiều cao
của khối trụ và khối nón cùng bằng
2cm
và bằng độ dài của đường kính đáy.
Kéo ô thích hợp thả vào vị trí tương ứng để hoàn thành các câu sau:
Thể tích gỗ cần dùng để làm khối đồ chơi gần bằng: [Vị trí thả 1]
3
cm
Một khách hàng muốn sơn khối đồ chơi đó bằng nhiều màu sắc khác nhau. Diện
tích bề mặt gỗ cần sơn gần bằng: [Vị trí thả 2]
2
cm
.
Nếu xưởng gỗ này muốn làm một chiếc hộp hình trụ bằng bìa cứng để đựng khối đồ chơi
đó sao cho đỉnh của khối nón trùng với tâm mặt đáy trên của hộp và đáy khối trụ vừa khít
với đáy dưới của hộp. Diện tích bìa cứng cần dùng gần bằng: [Vị trí thả 3]
2
cm
. (Các kết
quả làm tròn đến chữ số thập phân thứ hai).
Đáp án:
Thể tích gỗ cần dùng để làm khối đồ chơi gần bằng:
3
cm
Một khách hàng muốn sơn khối đồ chơi đó bằng nhiều màu sắc khác nhau. Diện tích bề
mặt gỗ cần sơn gần bằng:
2
cm
Nếu xưởng gỗ này muốn làm một chiếc hộp hình trụ bằng bìa cứng để đựng khối đồ chơi
đó sao cho đỉnh của khối nón trùng với tâm mặt đáy trên của hộp và đáy khối trụ vừa khít
với đáy dưới của hộp. Diện tích bìa cứng cần dùng gần bằng:
2
cm
. (Các kết quả
làm tròn đến chữ số thập phân thứ hai.
22,73
8,38
31,42
28,27
19,59
8,38
22,73
31,42