Đ 1ỀĐ KI M TRA CU I H C K IỀ Ể Ố Ọ Ỳ
MÔN TOÁN 12
Câu 1 (TH). G i ọM, m l n l t là giá tr l n nh t và giá tr nh nh t c a hàm s trên Tính t ng c aầ ượ ị ớ ấ ị ỏ ấ ủ ố ổ ủ
A. B. C. D.
Câu 2 (NB). Th tích c a kh i chóp có di n tích đáy là ể ủ ố ệ S và chi u cao ềh là:
A. B. C. D.
Câu 3 (TH). Tìm giá tr c a tham s ị ủ ố m đ đ th hàm s đi qua ể ồ ị ố
A. B. C. D.
Câu 4 (NB). T p xác đnh ậ ị D c a hàm s làủ ố
A. B. C. D.
Câu 5 (TH). Cho hàm s v i Tìm ố ớ m đ ể
A. B. C. D.
Câu 6 (NB). Ti m c n đng c a đ th hàm s làệ ậ ứ ủ ồ ị ố
A. B. C. D.
Câu 7 (TH). Ph ng trình có t p nghi m là:ươ ậ ệ
A. B. C. D.
Câu 8 (NB). Kh i l p ph ng c nh 2ố ậ ươ ạ a có th tích làể
A. B. C. D.
Câu 9 (NB). Cho hàm s M nh đ nào sau đây là đúng?ố ệ ề
A. Hàm s ngh ch bi n trên kho ng ố ị ế ả B. Hàm s ngh ch bi n trên ố ị ế
C. Hàm s đng bi n trên kho ng ố ồ ế ả D. Hàm s đng bi n trên ố ồ ế
Câu 10 (TH). Cho đng th c Khi đó thu c kho ng nào sau đây?ẳ ứ ộ ả
A. B. C. D.
Câu 11 (TH). Đ th hàm s và đng th ng có t t c bao nhiêu đi m chung?ồ ị ố ườ ẳ ấ ả ể
A. 2 B. 1 C. 0 D. 3
Câu 12 (NB). Cho hình tr có chi u cao ụ ề h và hình tròn đáy có bán kính R. Khi đó di n tích xung quanhệ
c a làủ
A. B. C. D.
Câu 13 (NB). Tìm ti m c n ngang c a đ th hàm s ệ ậ ủ ồ ị ố
A. B. C. D.
Câu 14 (TH). Cho hàm s Khi đó giá tr c a b ngố ị ủ ằ
A. B. C. 8 D.
Câu 15 (NB). Cho hàm s có b ng bi n thiên nh hình d i. Hàm s trên đng bi n trên kho ngố ả ế ư ướ ố ồ ế ả
nào d i đây?ướ
A. B. C. D.
Câu 16 (TH). Hàm s nào sau đây ngh ch bi n trên ?ố ị ế
A. B. C. D.
Câu 17 (NB). Th tích c a kh i lăng tr có di n tích đáy ể ủ ố ụ ệ S và chi u cao ềh là
A. B. C. D.
Câu 18 (TH). T p xác đnh ậ ị D c a hàm s làủ ố
A. B. C. D.
Câu 19 (NB). Th tích c a kh i nón tròn xoay có di n tích đáy ể ủ ố ệ B và chi u cao ềh là
A. B. C. D.
Câu 20 (NB). Th tích kh i h p ch nh t có ba kích th c ể ố ộ ữ ậ ướ a, 2a, 3a là
A. B. C. D.
Câu 21 (TH). Cho hàm s Đi m c c ti u c a hàm s làố ể ự ể ủ ố
A. 2018 B. 2019 C. 1 D. 0
Câu 22 (VD). Tìm t t c các giá tr th c c a tham s ấ ả ị ự ủ ố m đ hàm s đt c c đi t i ể ố ạ ự ạ ạ
A. B. C. D. Không t n t i ồ ạ m
Câu 23 (NB). Nghi m c a ph ng trình làệ ủ ươ
A. B. 2 C. D.
Câu 24 (TH). Đ th d i là đ th c a hàm s nào sau đây?ồ ị ướ ồ ị ủ ố
A. B. C. D.
Câu 25 (TH). Tính đo hàm c a hàm s ạ ủ ố
A. B. C. D.
Câu 26 (TH). Cho kh i lăng tr đng có di n tích đáy b ng , m t bên là hình vuông có Th tích kh iố ụ ứ ệ ằ ặ ể ố
lăng tr làụ
A. B. C. D.
Câu 27 (TH). N u thì b ngế ằ
A. 9 B. 21 C. 20 D. 13
Câu 28 (VD). Cho hàm s Khi đó nghi m c a ph ng trình làố ệ ủ ươ
A. B. C. D.
Câu 29 (TH). Trong không gian cho tam giác OIM vuông t i ạI, và Khi quay tam giác IOM quanh c nhạ
góc vuông OI thì đng g p khúc ườ ấ OMI t o thành m t hình nón tròn xoay có di n tích toàn ph n làạ ộ ệ ầ
A. B. C. D.
Câu 30 (VD). M t hình tr có hai đáy là hai hình tròn và . Kho ng cách gi a hai đáy là M t hình nónộ ụ ả ữ ộ
có đnh là và đáy là hình tròn . G i l n l t là di n tích xung quanh c a và Khi đó t s b ngỉ ọ ầ ượ ệ ủ ỉ ố ằ
A. B. 1 C. 2 D.
Câu 31 (TH). Ti p tuy n c a đ th hàm s t i đi m có hoành đ b ng 1 có ph ng trình làế ế ủ ồ ị ố ạ ể ộ ằ ươ
A. B. C. D.
Câu 32 (VD). Cho hàm s liên t c trên và có đo hàm Kh ng đnh nào sau đây là đúng?ố ụ ạ ẳ ị
A. Hàm s có 3 đi m c c tr .ố ể ự ị B. Hàm s có 6 đi m c c tr .ố ể ự ị
C. Hàm s có 2 đi m c c tr .ố ể ự ị D. Hàm s có 1 đi m c c tr .ố ể ự ị
Câu 33 (VD). Có bao nhiêu đi m ểM thu c đ th hàm s sao cho kho ng cách t ộ ồ ị ố ả ừ M đn tr c tungế ụ
b ng hai l n kho ng cách t ằ ầ ả ừ M đn tr c hoànhế ụ
A. 1 B. 3 C. 2 D. 0
Câu 34 (VD). Có bao nhiêu ti p tuy n v i đ th hàm s mà song song v i đng th ng ế ế ớ ồ ị ố ớ ườ ẳ
A. 2 B. 3 C. 0 D. 1
Câu 35 (VD). Trong không gian cho hình vuông ABCD c nh ạa. G i và ọH l n l t là trung đi m c aầ ượ ể ủ
các c nh ạAB và CD. Khi quay hình vuông ABCD, k c các đi m trong đó, xung quanh đng th ngể ả ể ườ ẳ
IH ta đc m t kh i tr tròn xoay có th tích làượ ộ ố ụ ể
A. B. C. D.
Câu 36 (TH). Cho hàm s xác đnh và liên t c trên các kho ng và . Đ th hàm s nh hình v d i.ố ị ụ ả ồ ị ố ư ẽ ướ
M nh đ nào sau đây là đúng?ệ ề
A. B. C. D.
Câu 37 (TH). Cho kh i chóp ốS.ABC có chi u cao b ng ề ằ a và đáy ABC là tam giác vuông cân t i ạA, . Thể
tích kh i chóp ốS.ABC là
A. B. C. D.
Câu 38 (VD). Tìm t t c các giá tr th c c a tham s ấ ả ị ự ủ ố m đ hàm s đng bi n trên kho ng ể ố ồ ế ả
A. B. C. D.
Câu 39 (VD). Bi t là đi m c c ti u c a đ th hàm s Tìm t a đ đi m c c đi c a đ th hàm sế ể ự ể ủ ồ ị ố ọ ộ ể ự ạ ủ ồ ị ố
đó.
A. B. C. D.
Câu 40 (VD). Cho kh i h p có th tích b ng và di n tích tam giác b ng Kho ng cách t đi m ố ộ ể ằ ệ ằ ả ừ ể A
đn m t ph ng b ngế ặ ẳ ằ
A. 3aB. 2aC. 6aD. a
Câu 41 (TH). Tìm t t c các giá tr th c c a tham s ấ ả ị ự ủ ố m đ giá tr l n nh t c a hàm s trên đo nể ị ớ ấ ủ ố ạ
b ng 11.ằ
A. B. C. D.
Câu 42 (VD). Giá tr l n nh t c a tham s ị ớ ấ ủ ố m đ ph ng trình có nghi m thu c kho ng nào sau đây?ể ươ ệ ộ ả
A. B. C. D.
Câu 43 (VD). Tìm t t c các giá tr th c c a tham s ấ ả ị ự ủ ố m đ đng th ng c t đ th hàm s t i 4 đi mể ườ ẳ ắ ồ ị ố ạ ể
phân bi t.ệ
A. B. C. D.
Câu 44 (VD). Xét các s th c d ng ố ự ươ a, b, c th a mãn và Khi đó b ngỏ ằ
A. B. C. D.
Câu 45 (VD). Cho kh i lăng tr có đáy ố ụ ABCD là hình thang cân, góc gi a hai m t ph ng và b ngữ ặ ẳ ằ
N u vuông góc v i m t ph ng thì kh i lăng tr có th tích làế ớ ặ ẳ ố ụ ể
A. B. C. D.
Câu 46 (VD). Bi t nghi m duy nh t c a ph ng trình có d ng trong đó ế ệ ấ ủ ươ ạ a, b, c là các s nguyênố
d ng và ươ a, c là các s nguyên t . Khi đó b ngố ố ằ
A. 8 B. 9 C. 11 D. 10
Câu 47 (TH). Cho hàm s Kh ng đnh nào sau đây là đúng?ố ẳ ị
A. B. C. D.
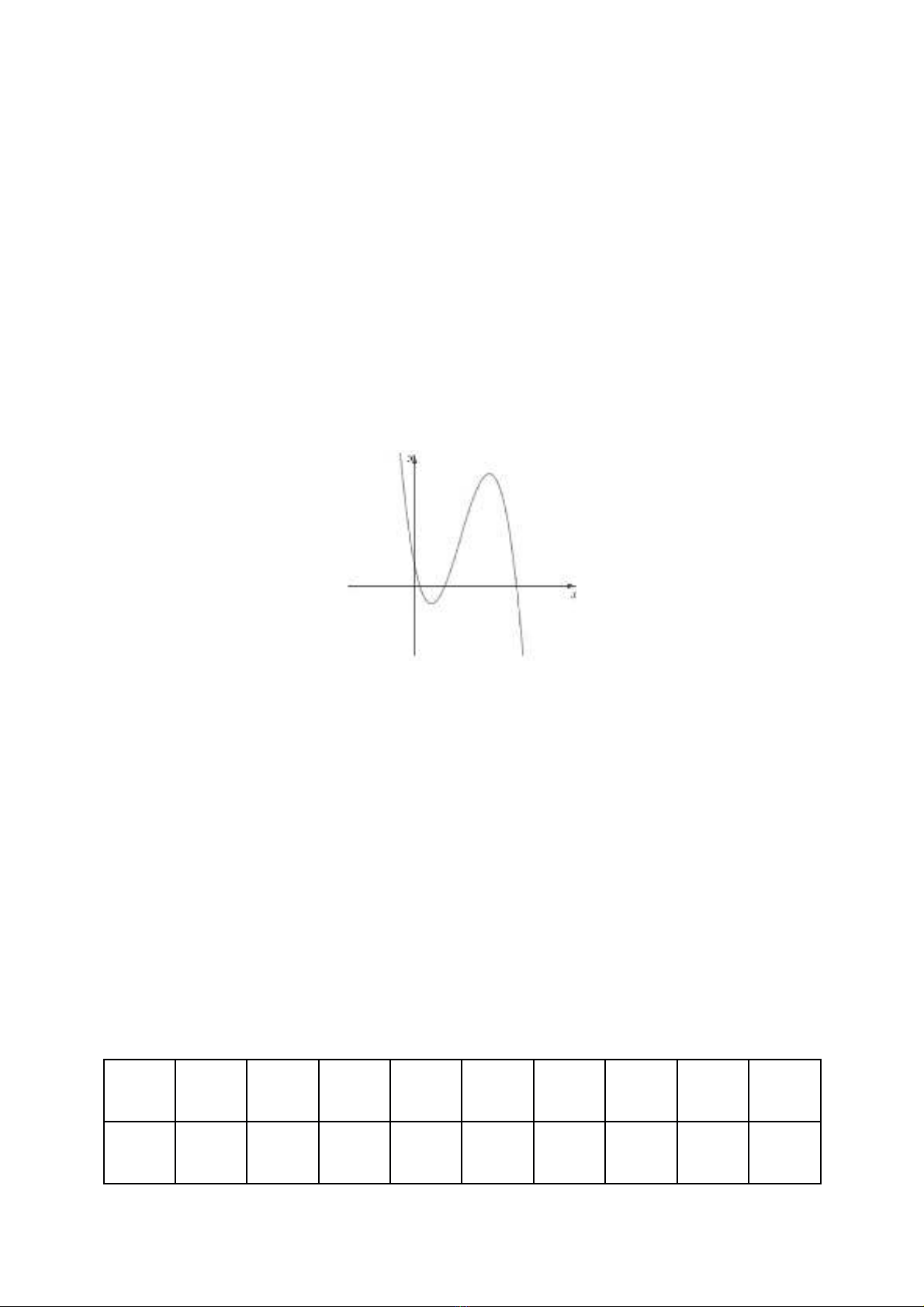
Câu 48 (VD). Cho hàm s có đ th nh hình v . Kh ng đnh nào sau đây là đúng?ố ồ ị ư ẽ ẳ ị
A. B.
C. D.
Câu 49 (VD). Cho kh i chóp ốS.ABCD có đáy ABCD là hình ch nh t và góc gi a ữ ậ ữ SB và m t ph ngặ ẳ
b ng Th tích kh i chóp làằ ể ố
A. B. C. D.
Câu 50 (VD). M t hình tr có chi u cao b ng ộ ụ ề ằ a và l n l t là tâm c a hai đáy. Hai đi m ầ ượ ủ ể A và B l nầ
l t n m trên hai đng tròn đáy sao cho N u kho ng cách gi a ượ ằ ườ ế ả ữ AB và b ng thì th tích c a kh iằ ể ủ ố
tr t o nên b i làụ ạ ở
A. B. C. D.
Đáp án
1-A 2-B 3-A 4-D 5-A 6-D 7-A 8-D 9-A 10-C
11-B 12-A 13-B 14-B 15-B 16-C 17-D 18-D 19-A 20-A