BỘ ĐỀ ÔN THI HỌC
KỲ II - TOÁN 12 -2021
CHƯƠNG
1
ĐỀ 1 - ÔN HỌC KỲ II - TOÁN 12 - 2021ĐỀ 1 - ÔN HỌC KỲ II - TOÁN 12 - 2021
1
CHỦ ĐỀ
A. TRẮC NGHIỆM
Câu 1. Trên mặt phẳng tọa độ, biết M(−1; 3) là điểm biểu diễn của số phức z. Phần thực của z
bằng
A−3.B−1.C3.D1.
Câu 2. Họ tất cả các nguyên hàm của hàm số y= 2021xlà
A2021x+C.B2021x+1
2021 +C.C2021x
ln 2021 +C.D2021xln 2021 + C.
Câu 3. Biết F(x)là một nguyên hàm của hàm số f(x) = sin 2xvà Fπ
4=−1. Tính Fπ
6.
AFπ
6=5
4.BFπ
6=√3−1.
CFπ
6=−5
4.DFπ
6=−√3
4−1.
Câu 4. Họ tất cả các nguyên hàm của hàm số f(x) = cos 2xlà
A1
2sin 2x+C.B−1
2sin 2x+C.C−2 sin 2x+C.D2 sin 2x+C.
Câu 5. Trong không gian Oxyz, phương trình mặt phẳng (Oyz)là
Ay= 0.Bz= 0.Cy+z= 1.Dx= 0.
Câu 6. Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 5; −4) và mặt phẳng (P): x+y−3z+3 =
0. Gọi Hlà hình chiếu vuông góc của Mtrên mặt phẳng (P). Khi đó cao độ của điểm Hlà
A2.B3.C−4.D5.
Câu 7. Gọi z1và z2lần lượt là nghiệm của phươngtrình: z2−2z+ 5 = 0. Tính P=|z1|2+|z2|2.
AP=√5.BP= 2√5.CP= 10.DP= 20.
Câu 8. Trong không gian Oxyz, hãy viết phương trình của đường thẳng dđi qua điểm M(−1; 0; 0)
và vuông góc với mặt phẳng (P): x+ 2y−z+ 1 = 0.
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
Ad:x+ 1
1=y
2=z
−1.Bd:x+ 1
1=y
2=z
1.
Cd:x−1
1=y
2=z
1.Dd:x−1
1=y
2=z
−1.
Câu 9. Cho F(x)là một nguyên hàm của f(x)trên Rvà F(0) = 2, F (3) = 7. Tính
3
Z
0
f(x) dx.
A−9.B−5.C9.D5.
Câu 10. Cho số phức z=a+bi (a, b ∈R).Mệnh đề nào dưới đây luôn đúng?
Az−¯z= 2a.Bz¯z=a2−b2.C|z2|=|z|2.Dz+ ¯z= 2bi.
Câu 11. Cho số phức z= 1 + 3i. Tìm phần thực của số phức z2.
A10 .B8 + 6i.C−8 + 6i.D−8.
Câu 12. Trong không gian Oxyz, cho mặt phẳng (P): −x+y+ 3z+ 1 = 0. Mặt phẳng song song
với mặt phẳng (P)có phương trình nào sau đây?
A2x−2y−6z+ 7 = 0.B−2x+ 2y+ 3z+ 5 = 0.
C−x−y+ 3z+ 1 = 0.Dx−y+ 3z−3 = 0.
Câu 13. Gọi (H)là hình phẳng giới hạn bởi các đường x= 3;y= 2; trục hoành và trục tung. Thể
tích khối tròn xoay sinh bởi (H)quay quanh trục hoành bằng
AV= 12π.BV= 36π.CV= 24π.DV= 18π.
Câu 14. Tìm nguyên hàm của hàm số f(x) = 3 cos x+1
x2trên (0; +∞).
A3 sin x−1
x+C.B3 cos x+ ln x+C.C−3 sin x+1
x+C.D3 cos x+1
x+C.
Câu 15. Cho tích phân I=Z3
1
f(x) dx= 8. Tính tích phân I=Z12
4
fx
4dx
AI= 12.BI= 2.CI= 32.DI= 3.
Câu 16. Cho hàm số y=f(x)có đạo hàm liên tục trên R, biết f(1) = 2017 và
2
Z
1
f′(x) dx= 1, giá
trị của f(2) bằng
A2017.B2016.C2019.D2018.
Câu 17. Tính mô-đun của số phức thoả mãn: z(2 −i) + 13i= 1.
A|z|= 34.B|z|=√34.C|z|=√34
3.D|z|=5√34
2.
Câu 18. Cho số phức zcó điểm biểu diễn trong mặt phẳng tọa độ Oxy là điểm M(1; −2). Tính
mô-đun của số phức w=i¯z−z2.
A6.B26.C√6.D√26.
Câu 19. Họ nguyên hàm của hàm số f(x) = xsin xlà
2
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
2
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
2
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
AF(x) = −xcos x+ sin x+C.BF(x) = xcos x−sin x+C.
CF(x) = xcos x+ sin x+C.DF(x) = −xcos x−sin x+C.
Câu 20. Cho tích phân I=
π
2
Z
0
√2 + cos x·sin xdx. Nếu đặt t= 2 + cos xthì kết quả nào sau đây
đúng?
AI=
π
2
Z
0
√tdt.BI= 2
2
Z
3
√tdt.CI=
2
Z
3
√tdt.DI=
3
Z
2
√tdt.
Câu 21. Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P)có véc-tơ pháp tuyến là #»
n=
(2; −1; 1). Véc-tơ nào sau đây cũng là véc-tơ pháp tuyến của (P)?
A(4; 2; −2).B(−2; 1; 1).C(4; −2; 2).D(−4; 2; 3).
Câu 22. Trong không gian Oxyz, cho các điểm I(1; 0; −1),A(2; 2; −3). Mặt cầu (S)tâm Ivà đi
qua điểm Acó phương trình là
A(x+ 1)2+y2+ (z−1)2= 3.B(x+ 1)2+y2+ (z−1)2= 9.
C(x−1)2+y2+ (z+ 1)2= 9.D(x−1)2+y2+ (z+ 1)2= 3.
Câu 23. Trong không gian Oxyz, cho đường thẳng d:x−2
−1=y−1
2=z
1. Đường thẳng dcó một
véc-tơ chỉ phương là
A#»
u2= (2; 1; 0).B#»
u3= (2; 1; 1).C#»
u1= (−1; 2; 1).D#»
u4= (−1; 2; 0).
Câu 24. Nguyên hàm của hàm số f(x) = √3x+ 2 là
A2
3
1
√3x+ 2 +C.B1
3(3x+ 2)√3x+ 2 + C.
C2
3(3x+ 2)√3x+ 2 + C.D2
9(3x+ 2)√3x+ 2 + C.
Câu 25. Diện tích hình phẳng giới hạn bởi các đường x= 0; x=πvà đồ thị y= sin x;y= cos x
được tính bởi biểu thức
AS=Zπ
0|cos x|dx.BS=Zπ
0(sin x−cos x) dx
.
CS=Zπ
0sin xdx.DS=Zπ
0|sin x−cos x|dx.
Câu 26. Trong mặt phẳng tọa độ Oxy, gọi M, N, P lần lượt là các điểm biểu diễn các số phức
z1= 1 + i,z2= 8 + i,z3= 1 −3i. Khẳng định nào sau đây là một mệnh đề đúng?
ATam giác MNP vuông cân. BTam giác MNP cân, không vuông.
CTam giác MNP đều. DTam giác MNP vuông, không cân.
Câu 27. Tìm số phức liên hợp của số phức zthỏa (−7 + 6i)z= 1 −2i.
Az=−19
85 +8
85i.Bz=19
85 +8
85i.Cz=19
85 −8
85i.Dz=−19
85 −8
85i.
Câu 28. Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol (P): y=x2và đường
thẳng d:y=xxoay quanh trục Ox bằng
3
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
3
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
3
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
Aπ
1
Z
0x2−xdx.Bπ
1
Z
0
x2dx−π
1
Z
0
x4dx.
Cπ
1
Z
0
x2dx+π
1
Z
0
x4dx.Dπ
1
Z
0x2−x2dx.
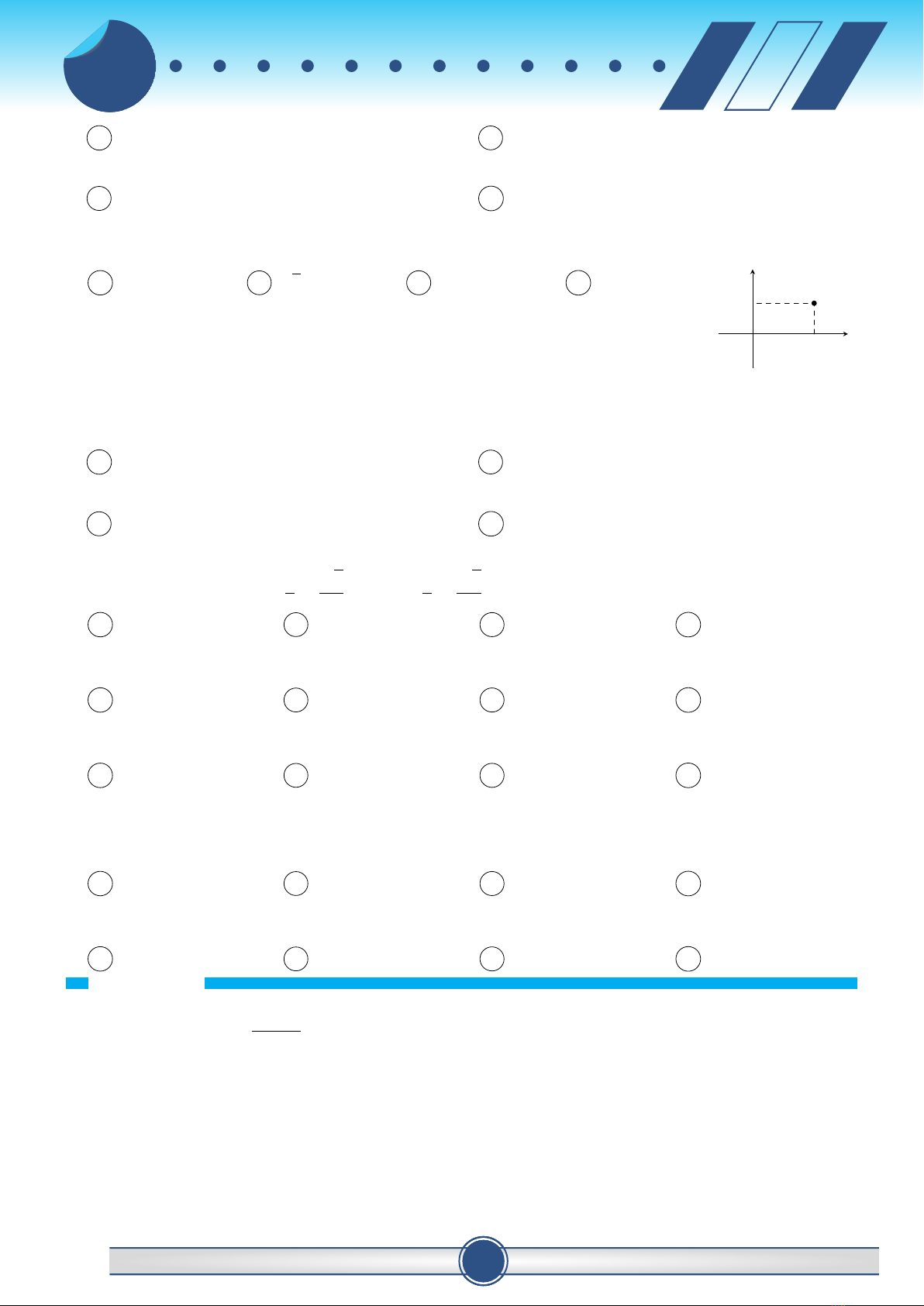
Câu 29. Điểm Mtrong hình vẽ bên biểu diễn số phức có phần thực là
A3.B√5.C2.D1.
x
y
O2
1M
Câu 30. Diện tích Scủa hình phẳng giới hạn bởi đồ thị của hàm số y=f1(x),y=f2(x)liên tục
và hai đường thẳng x=a,x=b(a < b) được tính theo công thức
AS=
b
Z
a|f1(x)−f2(x)|dx.BS=
b
Z
a
f1(x) dx−
b
Z
a
f2(x) dx.
CS=
b
Z
a
[f1(x)−f2(x)] dx.DS=
b
Z
a
[f1(x)−f2(x)] dx
.
Câu 31. Hai số phức z1=3
2+√7
2ivà z2=3
2−√7
2ilà nghiệm của phương trình nào sau đây?
Az2+ 3z−4 = 0.Bz2−3z+ 4 = 0.Cz2−3z−4 = 0.Dz2+ 3z+ 4 = 0.
Câu 32. Số phức có phần thực bằng 3và phần ảo bằng 4là
A4 + 3i.B3−4i.C3 + 4i.D4−3i.
Câu 33. Trong không gian Oxyz, cho điểm M(a;b;c), tọa độ của véc-tơ # »
MO là
A(−a;b;−c).B(−a;−b;−c).C(a;b;c).D(−a;b;c).
Câu 34. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(8; 9; 2),B(3; 5; 1),C(11; 10; 4).
Số đo góc Acủa tam giác ABC là
A150◦.B120◦.C60◦.D30◦.
Câu 35. Cho z1= 5 + 3i,z2=−8 + 9i. Tọa độ điểm biểu diễn hình học của z=z1+z2là
AN(−3; 12).BQ(3; 12).CM(14; −5).DP(3; −12).
B. TỰ LUẬN
Câu 36. Tích phân
2
Z
0
xdx
x2+ 3.
Câu 37. Trong không gian với hệ tọa độ Oxyz, mặt cầu (S): x2+y2+z2−2x−4y−20 = 0 và
mặt phẳng (α): x+ 2y−2z+ 7 = 0 cắt nhau theo một đường tròn có chu vi bằng bao nhiêu?
Câu 38. Một ô tô đang chạy với vận tốc 10 m/s thì người lái đạp phanh; từ thời điểm đó, ô tô
chuyển động chậm dần đều với vận tốc v(t) = −5t+ 10 (m/s), trong đó tlà khoảng thời gian tính
4
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
4
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
4
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
TNT
TNT
2021
Ths.Nguyễn Hữu Nhanh Tiến
Ó0945949933
bằng giây, kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển
bao nhiêu mét?
Câu 39. Biết rằng số phức zthỏa điều kiện w= (z+ 3 −i) (z+ 1 + 3i)là số thực. Giá trị nhỏ nhất
của |z|bằng bao nhiêu?
HẾT
5
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
5
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ
5
Ths.Nguyễn Hữu Nhanh Tiến Ó0795955456- Huế mộng mơ