ĐỀ 1
ĐỀ THI GIỮA HỌC KÌ 2
MÔN: TOÁN 9
Thời gian làm bài: 90 phút
I. TRẮC NGHIỆM (2 điểm):
Câu 1. Kết quả nào sau đây là căn bậc hai số học của 9?
A. 81 B. -81 C. 3 D.
3
Câu 2. Cho hàm số
 2
3
yx
2
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có giá trị dương khi x < 0.
B. Hàm số có giá trị nhỏ nhất là y = 0 khi x = 0.
C. Hàm số đồng biến khi x > 0 và nghịch biến khi x < 0.
D. Hàm số nghịch biến khi x > 0 và đồng biến khi x < 0.
Câu 3. Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và tạo thành
0
50AMB
. Khi
đó số đo cung bị chắn bởi góc ở tâm AOB là bao nhiêu?
A.
0
50
B.
0
40
C.
0
130
D.
0
80
.
Câu 4. Tứ giác ABCD nội tiếp trong một đường tròn. Nếu
0
BAC 70
thì số đo góc BDC là bao
nhiêu?
A. 1100 B. 700. C. 1600. D. 1400.
II. TỰ LUẬN (8 điểm):
Câu 5. Cho biểu thức:
1 x x
:
x x 1 x x





P
a) Tìm điều kiện xác định và rút gọn biểu thức P;
b) Tìm giá trị của biểu thức P khi x = 4;
c) Tìm x để biểu thức P có giá trị là
13
3
.
Câu 6. Giải bài toán sau bằng cách lập hệ phương trình:
Tìm một số có hai chữ số, biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5 và
nếu đem số đó chia cho tổng các chữ số của nó thì được thương là 7 và dư là 6.
Câu 7. Cho tam giác ABC vuông tại A, trên cạnh AC lấy điểm D (D ≠ A, D ≠ C). Đường
tròn tâm O đường kính DC cắt BC tại E (E ≠ C).
a) Chứng minh tứ giác ABED nội tiếp.
b) Đường thẳng BD cắt đường tròn (O) tại điểm thứ hai I. Chứng minh ED là tia phân giác
của góc AEI.
c) Giả sử
tanABC 2.
Tìm vị trí của D trên AC để EA là tiếp tuyến của đường tròn
đường kính DC.
Câu 8. Với x, y là các số dương thỏa mãn điều kiện
x 2y
.
Tìm giá trị nhỏ nhất của biểu thức:
22
xy
Mxy
.
-HẾT-
(ThÝ sinh kh«ng sö dông tµi liÖu; c¸n bé coi thi kh«ng gi¶i thÝch g× thªm.)
Họ và tên thí sinh..........................................................Số báo danh..............
ĐỀ 2
ĐỀ THI GIỮA HỌC KÌ 2
MÔN: TOÁN 9
Thời gian làm bài: 90 phút
Bài I: (2 điểm)
1. Tính giá trị của biểu thức A =
1
2
x
x
với
7 4 3x
;
2. Cho biểu thức B =
14
1 2 2
x x x
x x x x


với x
0;x
4
Chứng minh rằng B =
3
2x
;
3. Tìm x để P =
1
B
A
;
Bài II: (2 điểm)Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Tìm số tự nhiên có hai chữ số, biết tổng hai chữ số của nó bằng 9, nếu lấy số đó chia cho
số viết theo thứ tự ngược lại thì được thương là 2 và còn dư 18?
Bài III: (2 điểm)
1. Giải phương trình sau: 2x2 + (2 -
3
)x -
3
= 0
2. Cho parabol (P): y =
2
1
2x
và đường thẳng (d) có phương trình: y = - mx + 2
Chứng minh rằng:
m
(d) luôn cắt (P) tại hai điểm phân biệt A; B và SOAB
4
Bài IV: (3,5 điểm)Cho tam giác ABC vuông cân đỉnh A. Đường tròn đường kính AB cắt
BC tại D (D khác B). Điểm M bất kì trên đoạn AD, kẻ MH, MI lần lượt vuông góc với AB
và AC (H
AB; I
AC).
1) Chứng minh: Tứ giác MDCI nội tiếp;
2) Chứng minh:
MID MBC
;
3) Kẻ HK
(ID K
ID). Chứng minh: K; M; B thẳng hàng;
4) Khi M di động trên đoạn AD, chứng minh rằng đường thẳng HK luôn đi qua một
điểm cố định.
Bài V:(0,5 điểm) Cho a, b, c > 0. Chứng minh:
3 3 3
abc ab bc ca
b c a
;
Giám thị coi thi không giải thích gì thêm!
ĐỀ 3
ĐỀ THI GIỮA HỌC KÌ 2
MÔN: TOÁN 9
Thời gian làm bài: 45 phút
Câu 1 (4,0 điểm).
1. Cho hàm số
2
y ax
. Tìm a biết đồ thị hàm số đi qua điểm A(-1; 1)
2. Giải các phương trình sau:
a)
220xx
b)
23 2 0 xx
c)
15
1
22


x
xx
Câu 2 (2,0 điểm). (Giải bài toán bằng cách lập hệ phương trình)
Một hình chữ nhật có chiều dài hơn chiều rộng 20 m. Nếu gấp đôi chiều dài và gấp 3
lần chiều rộng thì chu vi của hình chữ nhật là 480 m. Tính chiều dài và chiều rộng ban đầu
của hình chữ nhật đó.
Câu 3 (3,0 điểm).
Cho phương trình
22 3 0. x mx
1) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m.
2) Gọi
12
, xx
là hai nghiệm của phương trình. Tìm m để
22
12
10xx
Câu 4 (1,0 điểm)
Cho parabol
2
P : y x
và đường thẳng
d : y 2 m 3 x 2m 2
Chứng minh rằng với mọi m parabol (P) và đường thẳng
d
luôn cắt nhau tại hai điểm
phân biệt. Tìm m sao cho hai giao điểm đó có hoành độ dương.
---------------------------HẾT---------------------------
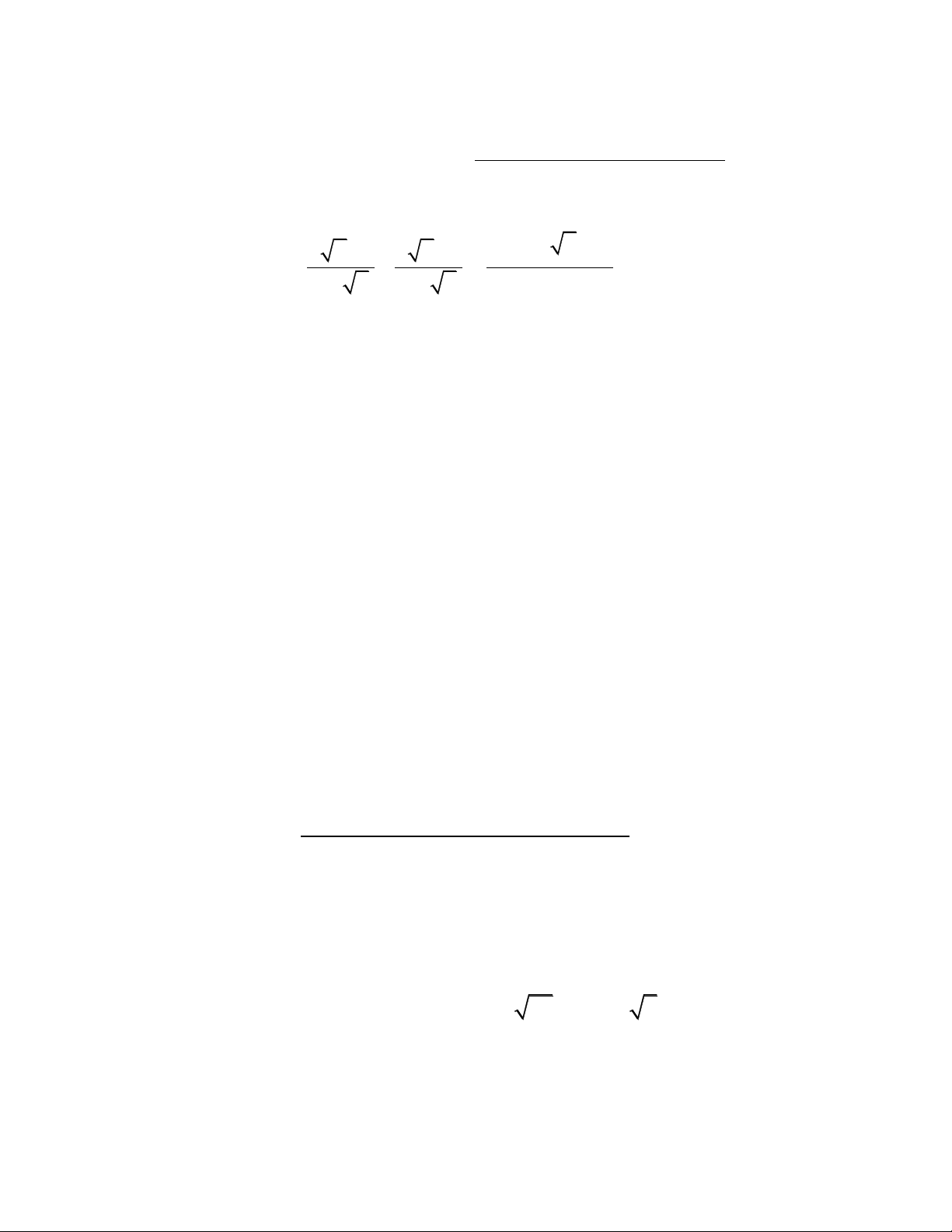
ĐỀ 4
ĐỀ THI GIỮA HỌC KÌ 2
MÔN: TOÁN 9
Thời gian làm bài: 90 phút
Câu 1 (2 điểm):
Cho biểu thức: A =
2 x 2 x 1
x x 1 x x 1 :
x1
x x x x







.
a) Rút gọn A.
b) Tìm x để A < 0.
Câu 2 (2,0 điểm): Giải bài toán bằng cách lập phương trình, hệ phương trình
Hai công nhân cùng sơn cửa cho một công trình trong 4 ngày thì xong công việc.
Nếu người thứ nhất làm một mình trong 9 ngày rồi người thứ hai đến cùng làm tiếp trong 1
ngày nữa thì xong công việc. Hỏi mỗi người làm một mình thì bao lâu xong việc?
Câu 3 (2,0 điểm):
Cho hệ phương trình:
mx y 5
2x y 2

(I)
a) Giải hệ (I) với m = 5.
b) Xác định giá trị của m để hệ phương trình (I) có nghiệm duy nhất và thỏa mãn: 2x + 3y
= 12
Câu 4 (3,5 điểm)
Cho nửa đường tròn tâm O đường kính AB và điểm M bất kì trên nửa đường tròn (M
khác A và B). Trên nửa mặt phẳng bờ AB chứa nửa đường tròn kẻ tiếp tuyến Ax. Tia BM
cắt Ax tại I; tia phân giác của góc IAM cắt nửa đường tròn tại E; cắt tia BM tại F; tia BE
cắt Ax tại H, cắt AM tại K.file word đề-đáp án Zalo 0986686826
1. Chứng minh rằng: AEMB là tứ giác nội tiếp và AI2 = IM.MB
2. Chứng minh BAF là tam giác cân
3. Chứng minh rằng tứ giác AKFH là hình thoi.
Câu 5 (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức:
P a 2 ab 3b 2 a 1
---------------------------HẾT---------------------------
ĐỀ 5
ĐỀ THI GIỮA HỌC KÌ 2
MÔN: TOÁN 9
Thời gian làm bài: 45 phút
Câu 1 (4,0 điểm). Giải các phương trình:
1)
2
x 8x 0
2)
2
x 2x 2 2 0
3)
2
3x 10x 8 0
4)
2
2x 2x 1 0
Câu 2 (5,0 điểm). Cho phương trình bậc hai:
2
x 6x 2m 1 0
(1). Tìm m để:
1) Phương trình (1) có nghiệm kép. Tính nghiệm kép đó.
2) Phương trình (1) có hai nghiệm trái dấu.
3) Phương trình (1) có một nghiệm là x = 2. Tìm nghiệm còn lại.
4) Phương trình (1) có hai nghiệm phân biệt
1
x
và
2
x
, thỏa mãn:
12
x x 4
Câu 3 (1,0 điểm). Chứng tỏ rằng parabol
2
yx
và đường thẳng
y 2mx 1
luôn cắt nhau
tại hai điểm phân biệt có hoành độ giao điểm là
1
x
và
2
x
. Tính giá trị biểu thức:
2
1 2 1 2
A x x x 2mx 3
.
---------------------------HẾT---------------------------