BỘ ĐỀ THI HỌC SINH GIỎI
MÔN TOÁN LỚP 6
CẤP TRƯỜNG NĂM 2020-2021
MỤC LỤC
1. Đề thi học sinh giỏi môn Toán lớp 6 cấp trường năm 2020-2021 có đáp án -
Trường THCS&THPT Trí Đức, TP HCM
2. Đề thi học sinh giỏi môn Toán lớp 6 cấp trường năm 2020-2021 - Trường
THCS Anh Sơn
3. Đề thi học sinh giỏi môn Toán lớp 6 cấp trường năm 2020-2021 - Trường
THCS Hải Thượng Lãn Ông
4. Đề thi học sinh giỏi môn Toán lớp 6 cấp trường năm 2020-2021 có đáp án -
Trường THCS Ngô Thị Nhậm
5. Đề thi học sinh giỏi môn Toán lớp 6 cấp trường năm 2020-2021 có đáp án -
Trường THCS Nguyễn Bỉnh Khiêm
6. Đề thi học sinh giỏi môn Toán lớp 6 cấp trường năm 2018-2019 có đáp án -
Trường THCS Nguyễn Trãi, Mộ Đức
SỞ GIÁO DỤC & ĐÀO TẠO TPHCM
TRƯỜNG THCS & THPT TRÍ ĐỨC
ĐỀ CHÍNH THỨC
KÌ THI HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2020-2021
MÔN: TOÁN KHỐI 6
Thời gian làm bài: 90 phút;
Mã đề thi
(Học sinh không được sử dụng tài liệu)
Họ và tên học sinh: ..........................................................................
Số báo danh: .............................
Câu 1. (5 điểm) Tìm số tự nhiên có hai chữ số, biết rằng ba lần chữ số hàng chục lớn hơn chữ số hàng đơn vị
11 đơn vị, và nếu viết hai chữ số ấy theo thứ tự ngược lại thì được một số mới (có hai chữ số) lớn hơn số cũ
9 đơn vị.
Câu 2. (4 điểm) Trong kì thi học sinh giỏi cấp trường, lớp 6A có 17 bạn được công nhận học sinh giỏi văn,
25 bạn học sinh giỏi toán. Tìm số học sinh vừa đạt giải văn và vừa đạt giải toán, biết lớp 6A có 45 bạn và có
13 bạn không đạt học sinh giỏi.
Câu 3. (3 điểm) Lớp 6C1 có 15 bạn nam và một số bạn nữ.Tất cả học sinh lớp 6C1 đều là học sinh bán trú
hoặc nội trú. Biết rằng lớp số học sinh bán trú nữ ít hơn số học sinh nội trú nam là 7 học sinh. Tính số học
sinh bán trú của lớp 6C1.
Câu 4. (3 điểm) Có bao nhiêu số tự nhiên có hai chữ số mà tổng các chữ số của mỗi số đó chia hết cho 3 mà
không chia hết cho 2? Giải thích.
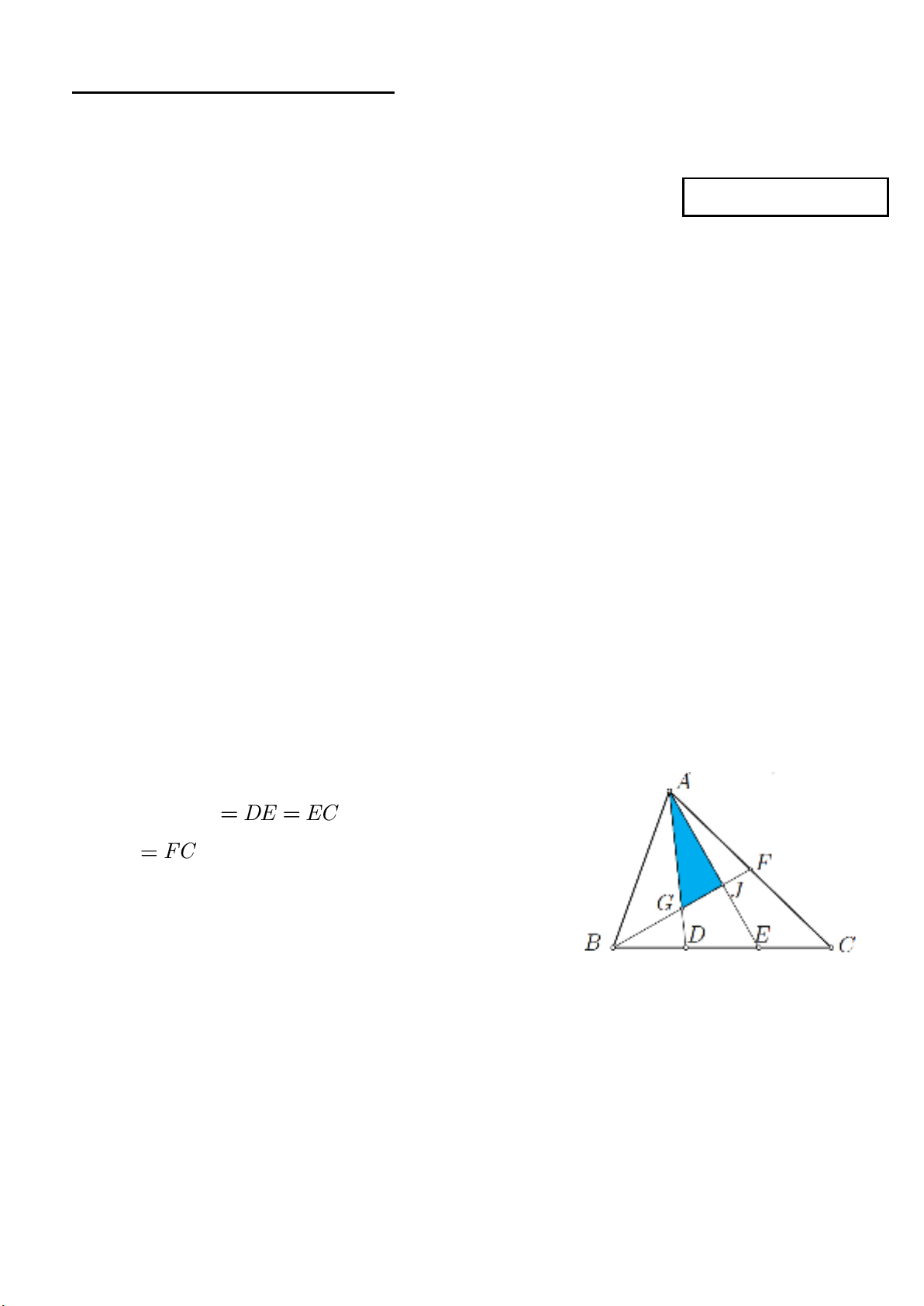
Câu 5. (5 điểm) Tam giác
ABC
có các diểm
trên cạnh
BC
sao cho
BD DE EC
và diểm
F
trên
AC
sao
cho
AF FC
. Biết rằng diện tích của
ABC
là
2
480cm
,
hãy tính diện tích của
a) tam giác
BGD
b) tam giác
.AGJ
Học sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
----------- HẾT ---------
-
HƯỚNG DẪN CHẤM ĐỀ THI HSG CẤP TRƯỜNG MÔN TOÁN LỚP 6
Câu
Đáp án
Điểm
Điểm
tổng
Câu 1
Gọi số tự nhiên cần tìm là
*
( , ; , 9)ab a b a b
Theo đề ra: 3a = b + 11 (1) và
9ba ab
9
10 10 9
10 10 9
9 9 9
1 (2)
ba ab
b a a b
b b a a
ba
ba

Từ (1) => b = 3a – 11 thay vào (2):
3a – 11 – a = 1
2a = 12, a = 6 thay vào (1) => b = 7
Số cần tìm là: 67
0,5
1,0
1,5
1,5
0,5
5 điểm
Câu 2
Số học sinh đạt cả 2 giải văn và toán là:
(17 25) (45 13) 42 32 10
(học sinh)
Vậy số học sinh đạt cả hai môn là 10 học sinh
4,0
4 điểm
Câu 3
Gọi x là số học sinh bán trú nam suy ra số học sinh nội trú nam là 15 – x
Suy ra số học sinh bán trú nữ là: 15 – x – 7 =8 – x
Vậy số học sinh bán trú của lớp 6C1 là: x + 8 – x = 8 học sinh
1,0
1,0
1,0
3 điểm
Câu 4
Xét các số
ab
mà
ab
chia hết cho 3:
Với
{3,6,9}a
và
{0,3,6,9}b
, có
3.4 12
số
ab
.
Với
{1,4,7}, {2,5,8}ab
, có
2.3.3 18
số
ab
.
Do đó, có
12 18 30
số
ab
mà
ab
chia hết cho 3 .
Tiếp theo ta đếm số số
ab
mà
ab
chia hết cho 6. Xét các trường hợp
sau:
- Với
6a
và
{0,6}b
, có 2 số
ab
.
- Với
5a
và
{1,7}b
hoặc hoán vị lại. Có 4 số
ab
.
- Với
4a
và
{2,8}b
hoặc hoán vị lại. Có 4 số
ab
.
1,5
3 điểm
- Với
{3,9}a
và
{3,9}b
, có 4 số
ab
.
Do đó, có
2 4 4 4 14
số
ab
mà
ab
chia hết cho
6.
Vậy
có
30 14 16
số thỏa mãn đề bài.
1,0
0,5
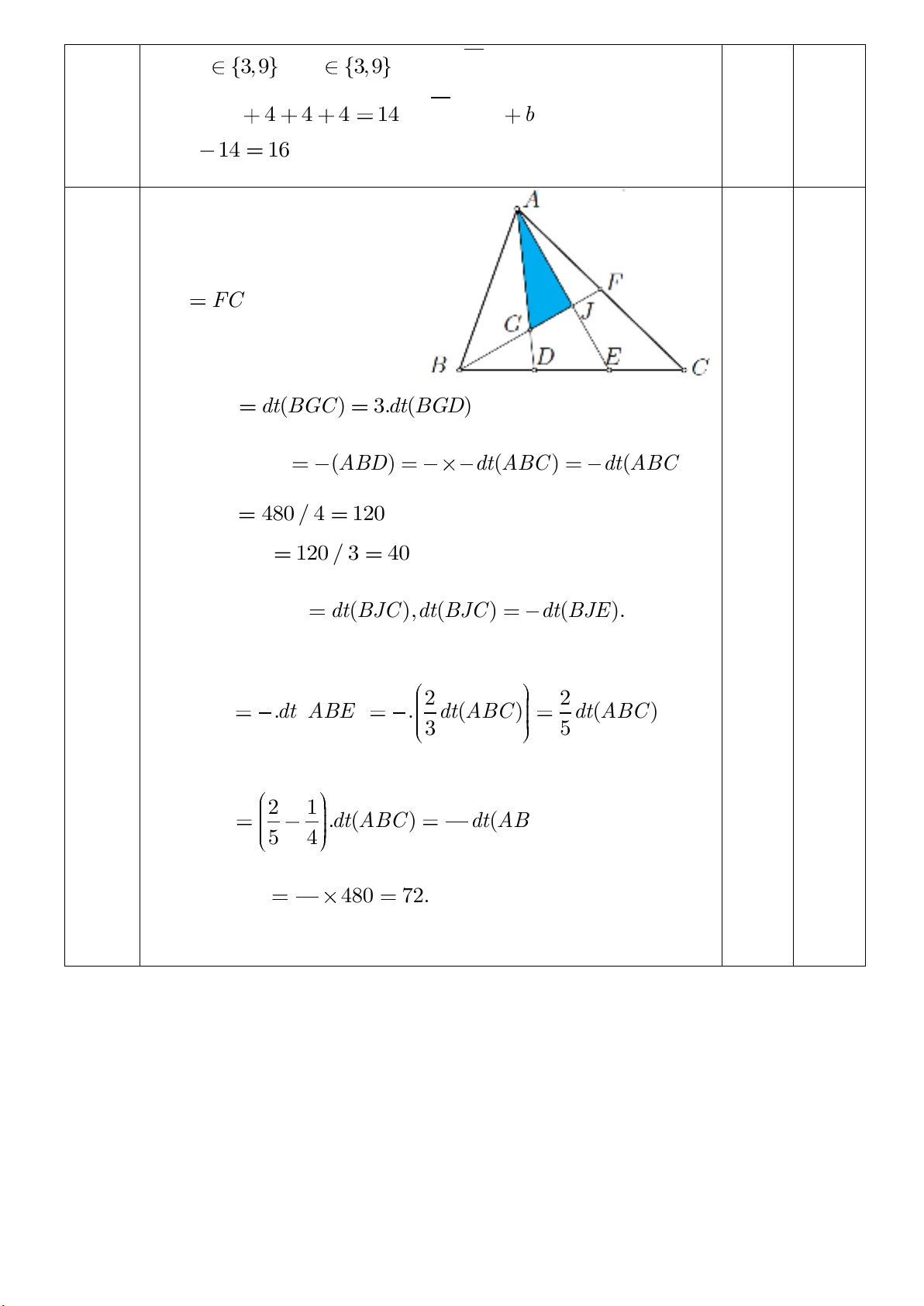
Câu 5
Tam giác
ABF
và
BCF
có
diện tích bằng nhau vì chung
chiều cao từ đỉnh
B
. Lại có
AF FC
, nên khoảng cách
vuông góc từ
,AC
đến
BF
bằng
nhau. Do đó,
( ) ( ) 3. ( )dt ABG dt BGC dt BGD
Suy ra
3 3 1 1
( ) ( ) ( ) ( ).
4 4 3 4
dt ABG ABD dt ABC dt ABC
( ) 480 / 4 120dt BAG
Nên
( ) 120 / 3 40dt BGD
Hơn nữa,
3
( ) ( ), ( ) ( ).
2
dt ABJ dt BJC dt BJC dt BJE
Suy ra
3 3 2 2
( ) . . ( ) ( )
5 5 3 5
dt ABJ dt ABE dt ABC dt ABC
.
Do đó,
2 1 3
( ) . ( ) ( )
5 4 20
dt AGJ dt ABC dt ABC
.
Vậy
3
( ) 480 72.
20
dt AGJ
1,0
1,0
1,0
1,0
1,0
5 điểm