Thí nghi m v t lý 1ệ ậ
CÁC BÀI THÍ NGHI M V T LÝ 1Ệ Ậ
§1. LÝ THUY T SAI SẾ Ố
I. Phép đo các đ i l ng v t lýạ ượ ậ
M i tính ch t v t lý c a các đ i t ng v t ch t đ c d c tr ng b i m t đ i l ngỗ ấ ậ ủ ố ượ ậ ấ ượ ặ ư ở ộ ạ ượ
v t lý. Đ xác đ nh đ nh tính và đ nh l ng các tính ch t v t lý, ng i ta ph i ti n hànhậ ể ị ị ị ượ ấ ậ ườ ả ế
phép đo các đ i l ng v t lý.ạ ượ ậ
Phép đo m t đ i l ng v t lý là phép so sánh nó v i m t đ i l ng cùng lo i đ cộ ạ ượ ậ ớ ộ ạ ượ ạ ượ
qui c ch n làm đ n v đo.ướ ọ ơ ị
Mu n th c hi n phép đo, ng i ta ph i xây d ng lý thuy t c a các ph ng pháp đoố ự ệ ườ ả ự ế ủ ươ
và s d ng các d ng c đo.ử ụ ụ ụ
II. Sai s c a phép đo các đ i l ng v t lýố ủ ạ ượ ậ
Đ nh y và đ chính xác c a các d ng c đo b gi i h n, giác quan c a ng i làmộ ạ ộ ủ ụ ụ ị ớ ạ ủ ườ
thí nghi m thi u nh y c m, đi u ki n c a các l n đo không n đ nh, ph ng pháp đo cóệ ế ạ ả ề ệ ủ ầ ổ ị ươ
tính ch t g n đúng,…. Do đó không th đo chính xác tuy t đ i giá tr th c c a đ i l ngấ ầ ể ệ ố ị ự ủ ạ ượ
v t lý c n đo, nói cách khác là k t qu c a phép đo có sai s . Nh v y khi ti n hành phépậ ầ ế ả ủ ố ư ậ ế
đo, không nh ng chúng ta ph i xác đ nh giá tr c a đ i l ng c n đo mà ph i xác đ nh cữ ả ị ị ủ ạ ượ ầ ả ị ả
sai s c a k t qu đo.ố ủ ế ả
Có nhi u lo i sai s gây b i các nguyên nhân khác nhau.ề ạ ố ở
- Sai s ng u nhiên: là lo i sai s khi n cho k t qu đo khi thì l n h n, khi thì nhố ẫ ạ ố ế ế ả ớ ơ ỏ
h n giá tr th c c a đ i l ng c n đo. Thí d khi đo th i gian chuy n đ ng c a v t r i tơ ị ự ủ ạ ượ ầ ụ ờ ể ộ ủ ậ ơ ự
do, chúng ta không th b m đ ng h đúng th i đi m v t b t đ u r i và th i đi m v t b tể ấ ồ ồ ờ ể ậ ắ ầ ơ ờ ể ậ ắ
đ u ch m đ t mà th ng b m s m h n ho c ch m h n các th i đi m này. Rõ ràng khôngầ ạ ấ ườ ấ ớ ơ ặ ậ ơ ờ ể
th kh đ c sai s ng u nhiên, nh ng chúng ta có th gi m nh giá tr c a nó b ng cáchể ử ượ ố ẫ ư ể ả ỏ ị ủ ằ
th c hi n phép đo nhi u l n trong cùng đi u ki n và xác đ nh giá tr trung bình c a nó d aự ệ ề ầ ề ệ ị ị ủ ự
trên c s c a phép tính xác su t th ng kê.ơ ở ủ ấ ố
- Sai s d ng c : là sai s do b n thân d ng c , thi t b đo gây ra.ố ụ ụ ố ả ụ ụ ế ị
- Sai s h th ng: Là sai s làm cho k t qu đo ho c bao gi cũng l n h n ho cố ệ ố ố ế ả ặ ờ ớ ơ ặ
bao gi cũng nh h n giá tr th c c a đ i l ng c n đo. Sai s h th ng th ng do ng iờ ỏ ơ ị ự ủ ạ ượ ầ ố ệ ố ườ ườ
làm th c nghi m thi u c n th n, do d ng c đo ch a đ c hi u ch nh đúng. Vì th sai sự ệ ế ẩ ậ ụ ụ ư ượ ệ ỉ ế ố
h th ng là lo i sai s có th kh đ c. ệ ố ạ ố ể ử ượ
Tóm l i khi làm thí nghi m chúng ta ch c n bi t cách xác đ nh hai lo i sai s là saiạ ệ ỉ ầ ế ị ạ ố
s ng u nhiên và sai s d ng c .ố ẫ ố ụ ụ
III. Cách xác đ nh sai s c a phép đo các đ i l ng tr c ti pị ố ủ ạ ượ ự ế
Phép đo các đ i l ng đo tr c ti p là phép đo mà k t qu c a nó đ c đ c tr cạ ượ ự ế ế ả ủ ượ ọ ự
ti p ngay trên thang đo c a d ng c đo.ế ủ ụ ụ
G a s đ i l ng c n đo F có giá tr chính xác là A. N u đo tr c ti p đ i l ng nàyỉ ử ạ ượ ầ ị ế ự ế ạ ượ
n l n trong cùng đi u ki n, ta s nh n đ c các giá tr Aầ ề ệ ẽ ậ ượ ị 1, A2, A3,…,An nói chung khác v iớ
giá tr A, nghĩa là m i l n đo đ u có sai s .ị ỗ ầ ề ố
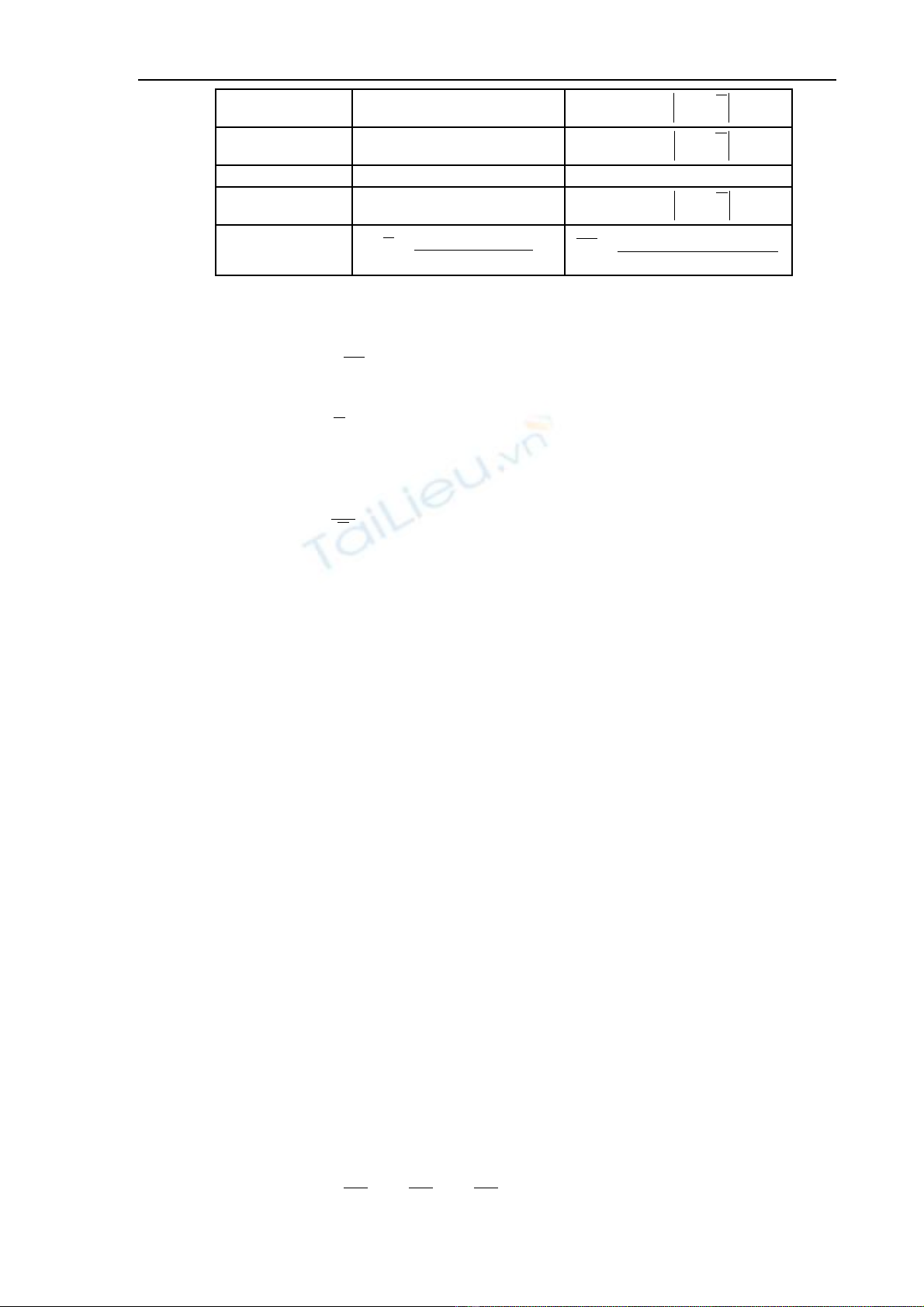
L n đoầGía tr đo đ cị ượ Sai s c a m i l n đoố ủ ỗ ầ
1 A1
AAA −=∆ 11
7
Thí nghi m v t lý 1ệ ậ
2 A2
AAA −=∆ 22
3 A3
AAA −=∆ 33
n An
AAA nn −=∆
TB
n
AAA
An
+++
=...
21
n
AAA
An
∆++∆+∆
=∆ ...
21
Sai s tuy t đ i c a phép đo đ c xác đ nh b ng t ng s h c c a sai s trung bìnhố ệ ố ủ ượ ị ằ ổ ố ọ ủ ố
c a t t c các l n đo và sai s d ng c :ủ ấ ả ầ ố ụ ụ
dc
AAA ∆+∆=∆
Nh v y giá tr c a đ i l ng c n đo đ c vi t:ư ậ ị ủ ạ ượ ầ ượ ế
AAA ∆±=
Đ chính xác c a k t qu đo đ i l ng F đ c đánh giá b ng sai s t ng đ i c aộ ủ ế ả ạ ượ ượ ằ ố ươ ố ủ
đ i l ng c n đo F, đó là t s gi a sai s tuy t đ i c a phép đo v i giá tr trung bình:ạ ượ ầ ỷ ố ữ ố ệ ố ủ ớ ị
(%)
IV. Cách xác đ nh sai s d ng cị ố ụ ụ
1. Thông th ng, sai s d ng c (không k thi t b đo đi n và thi t b đo hi n s )ườ ố ụ ụ ể ế ị ệ ế ị ệ ố
l y giá tr b ng m t đ chia nh nh t c a d ng c đo.ấ ị ằ ộ ộ ỏ ấ ủ ụ ụ
2. Đ i v i các đ ng h đo đi n thì sai s d ng c đ c tính theo công th c sau:ố ớ ồ ồ ệ ố ụ ụ ượ ứ
( )
max
%AAdc
δ
=∆
Trong đó δ là c p chính xác c a thang đo (ghi trên m t thang đo), Aấ ủ ặ max là giá tr c cị ự
đ i trên thang đo c a d ng c .ạ ủ ụ ụ
3. Sai s d ng c c a các thi t b đo hi n s đ c xác đ nh theo công th c sau:ố ụ ụ ủ ế ị ệ ố ượ ị ứ
( )
αδ
nAAdc +=∆ %
Trong đó δ là c p chính xác c a thang đo (ghi trên m t thang đo), A là giá tr hi n thấ ủ ặ ị ể ị
trên màn hình, α là đ phân gi i c a thang đo, n là m t s nguyên ph thu c vào d ng cộ ả ủ ộ ố ụ ộ ụ ụ
đo đ c qui đ nh b i nhà s n xu t.ượ ị ở ả ấ
V. Cách xác đ nh sai s đ i v i phép đo các đ i l ng đo gián ti pị ố ố ớ ạ ượ ế
1. Phép đo các đ i l ng đo gián ti p là phép đo mà k t qu c a nó đ c xác đ nhạ ượ ế ế ả ủ ượ ị
gián ti p thông qua công th c bi u di n quan h hàm s gi a đ i l ng c n đo v i các đ iế ứ ể ễ ệ ố ữ ạ ượ ầ ớ ạ
l ng đo tr c ti p khác. Thí d : v n t c c a chuy n đ ng th ng đ u đ c xác đ nh giánượ ự ế ụ ậ ố ủ ể ộ ẳ ề ượ ị
ti p thông qua công th c v = s/t, trong đó đ ng đi s có th đo tr c ti p b ng th c, th iế ứ ườ ể ự ế ằ ướ ờ
gian chuy n đ ng t đo tr c ti p b ng đ ng h .ể ộ ự ế ằ ồ ồ
2. Cách xác đ nh sai s c a phép đo gián ti p: Gi s đ i l ng c n đo F liên hị ố ủ ế ả ử ạ ượ ầ ệ
v i các đ i l ng đo tr c ti p x, y, z theo hàm s :ớ ạ ượ ự ế ố
F = f(x, y, z)
Khi đó sai s tuy t đ i c a đ i l ng F có th xác đ nh theo phép tính vi phân:ố ệ ố ủ ạ ượ ể ị
dz
z
F
dy
y
F
dx
x
F
dF ∂
∂
+
∂
∂
+
∂
∂
=
8
Thí nghi m v t lý 1ệ ậ
Thay các d u vi phân “d” b ng d u “Δ”, vì không bi t rõ chi u thay đ i c a các giáấ ằ ấ ế ề ổ ủ
tr F nên ta ph i ch n giá tr l n nh t c a sai s b ng cách l y t ng tr s tuy t đ i c a cácị ả ọ ị ớ ấ ủ ố ằ ấ ổ ị ố ệ ố ủ
vi phân riêng ph n:ầ
z
z
F
y
y
F
x
x
F
F∆
∂
∂
+∆
∂
∂
+∆
∂
∂
=∆
Sai s t ng đ i cũng có th tính theo phép vi phân nh sau:ố ươ ố ể ư
- Tính loganêpe c a hàm F= f(x, y, z) là lnF = lnf(x, y, z)ủ
- Tính vi phân toàn ph n c a lnF: d(lnF)= dF/Fầ ủ
- Rút g n bi u th c c a vi phân toàn ph n dF/F b ng cách g p nh ng vi phân riêngọ ể ứ ủ ầ ằ ộ ữ
ph n ch a cùng vi phân c a bi n dx ho c dy ho c dzầ ứ ủ ế ặ ặ
- L y t ng giá tr tuy t đ i c a các vi phân riêng ph n. Thay d u vi phân “d” b ngấ ổ ị ệ ố ủ ầ ấ ằ
d u sai s “Δ”, đ ng th i thay x, y, z, b ng các giá tr trung bình c a chúng.ấ ố ồ ờ ằ ị ủ
Thí d : Đo l c ma sát tr c quay theo công th c: ụ ự ổ ụ ứ
21
21
.hh
hh
mgfms +
−
=
, v i m, hớ1, h2 là các
đ i l ng đo tr c ti pạ ượ ự ế
B c 1:ướ lnfms = lnm + lng + ln(h1-h2) - ln(h1+h2)
B c 2ướ : tính vi phân toàn ph n c a lnfầ ủ ms theo công th c:ứ
( ) ( )
21
21
21
21
hh
hhd
hh
hhd
g
dg
m
dm
f
df
ms
ms
+
+
−
−
−
++=
B c 3:ướ Rút g n bi u th c vi phân toàn ph n:ọ ể ứ ầ
( )
2
2
2
1
2112
2
hh
dhhdhh
g
dg
m
dm
f
df
ms
ms
−
−
++=
B c 4:ướ L y t ng giá tr tuy t đ i c a các vi phân riêng ph n, Thay d u vi phân “d”ấ ổ ị ệ ố ủ ầ ấ
b ng d u sai s “Δ”, đ ng th i thay m,hằ ấ ố ồ ờ 1, h2 b ng các giá tr trung bình c a chúng.ằ ị ủ
( )
2 1 1 2
2 2
1 2
2
ms
ms
h h h h
fm g
g
f m h h
ε
∆ + ∆
∆∆ ∆
= = + + −
Trong đó:
21
21
hh
hh
gmf ms +
−
=
msms ff .
ε
=∆
VI. Ph ng pháp bi u di n k t qu đo b ng đ thươ ể ễ ế ả ằ ồ ị
Ph ng pháp bi u di n k t qu đo b ng đ th đ c ng d ng nhi u trong thíươ ể ễ ế ả ằ ồ ị ượ ứ ụ ề
nghi m v t lý, ph ng pháp này cho phép th hi n m t cách tr c quan s ph thu cệ ậ ươ ể ệ ộ ự ự ụ ộ
hàm s c a m t đ i l ng v t lý này vào m t đ i l ng v t lý khác. ố ủ ộ ạ ượ ậ ộ ạ ượ ậ
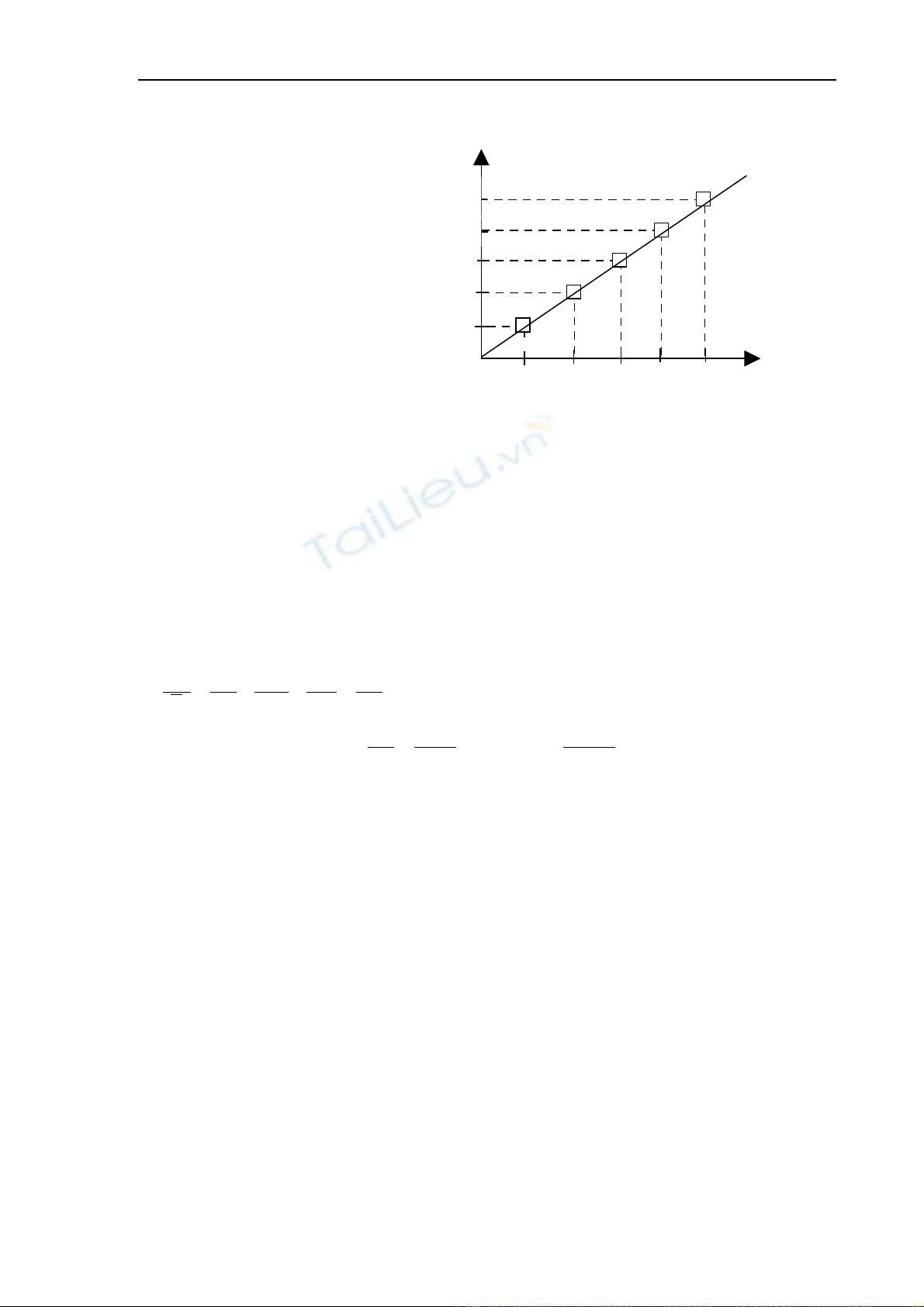
Thí d nghiên c u s ph thu c c a đi n tr R vào nhi t đ t, chúng ta có các s li uụ ứ ự ụ ộ ủ ệ ở ệ ộ ố ệ
ghi trong b ng d i đây:ả ướ
T(1000C) 0,0±0,1 1,0±0,1 2,0±0,1 3,0±0,1 4,0±0,1
R(Ω) 20 ± 2 40 ± 3 60 ± 2 80 ± 2 100 ± 3
9
1
2
3
4
5
t(1000C)
20
40
60
80
100
120
R(Ω
)
Thí nghi m v t lý 1ệ ậ
Căn c vào b ng s li u trênứ ả ố ệ
v đ thẽ ồ ị
- V h tr c t a đ , ch n tẽ ệ ụ ọ ộ ọ ỷ
l thích h pệ ợ
- V i m i c p R, t t ngớ ỗ ặ ươ
ng v m t đi m trên đứ ẽ ộ ể ồ
th , v ô bao sai s c a t vàị ẽ ố ủ
R
- V đ ng bi u di n thànhẽ ườ ể ễ
m t đ ng liên t c sao choộ ườ ụ
đi qua ô bao sai số
L u ý: ư
1. Qui t c làm tròn s :ắ ố
Vi c làm tròn s theo qui c sau: các ph n b đi ho c thêm vào ph i nh h n 1/10 giáệ ố ướ ầ ỏ ặ ả ỏ ơ
tr c a ph n g c. thí d : 0,7328 làm tròn thành 0,7 vì ph n b đi b ng 0,0328<1/10 c aị ủ ầ ố ụ ầ ỏ ằ ủ
0,7328; 0,2674 làm tròn thành 0,27 vì ph n thêm vào b ng 0,0026< 1/10 c a 0,2674ầ ằ ủ
2. Sai s c a h ng số ủ ằ ố: Đ i v i h ng s nh π, g, e,… thì l y giá tr c a h ng s đ nố ớ ằ ố ư ấ ị ủ ằ ố ế
ch s mà sai s t ng đ i c a h ng s nh h n ho c b ng 1/10 giá tr c a ít nh tữ ố ố ươ ố ủ ằ ố ỏ ơ ặ ằ ị ủ ấ
m t sai s t ng d i khác có trong công th c tính.ộ ố ươ ố ứ
Thí d : ta có công th c:ụ ứ
0086,0
1,50
1,0
2,30
2,0 +
∆
=++
∆
=
∆
π
π
π
π
V
V
Ta ph i l y π = 3,142 đ ả ấ ể
10
0086,0
000318,0
142,3
001,0 <==
∆
π
π
H NG D N H C THÍ NGHI MƯỚ Ẫ Ọ Ệ
1. Đ c bài thí nghi m đ hi u đ c c s lý thuy t, ph ng pháp đo.ọ ệ ể ể ượ ơ ở ế ươ
2. Yêu c u chu n b bài ra gi y tr c khi đ n phòng thí nghi m:ầ ẩ ị ấ ướ ế ệ
- Vi t m c đích, yêu c u c a bài thí nghi mế ụ ầ ủ ệ
- Vi t c s lý thuy t c a ph ng pháp đoế ơ ở ế ủ ươ
- Tr l i các câu h i cu i bàiả ờ ỏ ố
- Chu n b m u báo cáo thí nghi mẩ ị ẫ ệ
3. Lên phòng thí nghi m: Làm theo các b c h ng d n trong ph n ệ ướ ướ ẫ ầ Trình t thí nghi m,ự ệ
đo ra k t qu , x lý s li u, tính sai s , v đ th (n u có) và n p l i báo cáo.ế ả ử ố ệ ố ẽ ồ ị ế ộ ạ
10