Cấu trúc dữ liệu và giải thuật - Chương 6

Chia sẻ: Nguyễn Nhi | Ngày: | Loại File: PDF | Số trang:14

Thêm vào BST

Báo xấu

135
lượt xem 18
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

ĐỒ THỊ I. ĐỊNH NGHĨA VÀ MỘT SỐ KHÁI NIỆM Một đồ thị G(V,E) là 1 tập bao gồm 2 tập con : - Tập hữu hạn V, không rỗng, của các phân tử mà ta gọi là đỉnh (vertices). - Tập hữu hạn E, của các cặp đỉnh, mà mỗi cặp ta gọi là 1 cung (edge). Bản đồ đường bộ giữa các thành phố trong 1 khu vực là 1 đồ thị với thành phố là đỉnh, đường lối trong thời gian đó là cung. Mạng máy tính của 1 công ty, sơ đồ mạch điện của 1...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Cấu trúc dữ liệu và giải thuật - Chương 6

Chương VI. ĐỒ THỊ I. ĐỊNH NGHĨA VÀ MỘT SỐ KHÁI NIỆM Mộ t đồ thị G(V,E) là 1 tập bao gồm 2 tập con : - Tập hữu h ạn V, không rỗng, của các phân tử mà ta gọi là đỉnh (vertices). - Tập h ữu hạn E, của các cặp đỉnh, mà mỗi cặp ta gọi là 1 cung (edge). Bản đồ đường bộ giữa các thành phố trong 1 khu vự c là 1 đồ thị với thành phố là đ ỉnh, đường lối trong thời gian đó là cung. Mạng máy tính của 1 công ty, sơ đồ mạch điện của 1 khu chung cư, cấu trúc phân tử của các hợp chất hữu cơ v.v…tất cả đ ều có dạng đồ thị. Nếu u và v là 2 đỉnh trên đồ th ị mà thứ tự được phân biệt trong từng cặp, nghĩa vụ là (u, v) khác với (v, u) thì đồ thị được gọ i là đồ thị có hướng (directed graph). Lúc đó (u, v)được gọi là cung từ u tới v còn (v, u) được gọ i là cung từ v tới u. Nếu thứ tự 2 đỉnh củ a 1 cung không được coi trọng thì đồ thị được gọi là đồ th ị vô h ướng (undirected grap) và (u, v)được gọ i là cung giữa u và v hoặc cung giữa v và u. Trên hình vẽ cung có hướng được biểu diễn bằng mũ i tên còn cung vô hướng thì bằng 1 đoạn thẳng. 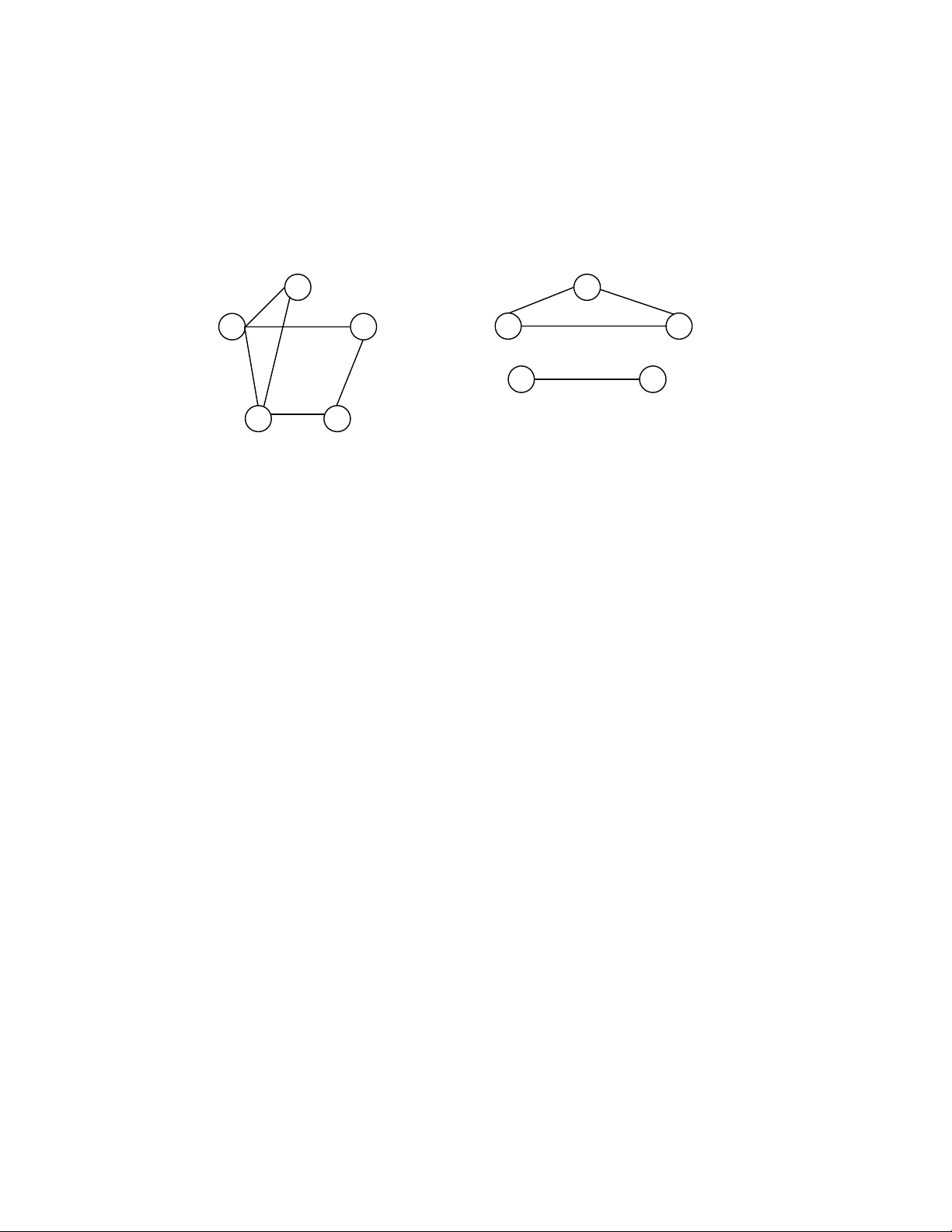Hình 6.1 minh ho ạ 1 số đồ thị :G1, G2 là các đồ th ị có hướng ; G3, G4 là các đồ thị vô h ướng. Ở đây ta quy ước : các đỉnh được đánh số từ 1 tới n (nếu đồ th ị có n đỉnh). Nếu trên đồ thị G (V,E) có 1 cung đi từ u tới v thì ta nói : v là đỉnh lân cận của u hay là đ ỉnh kề (adjacent) của u. Tất nhiên với đồ thị vô h ướng, khi có cung giữa 2 đỉnh, thì ta nói đ ỉnh này là lân cận của đỉnh kia. 1 1 2 2 3 3 4 G1
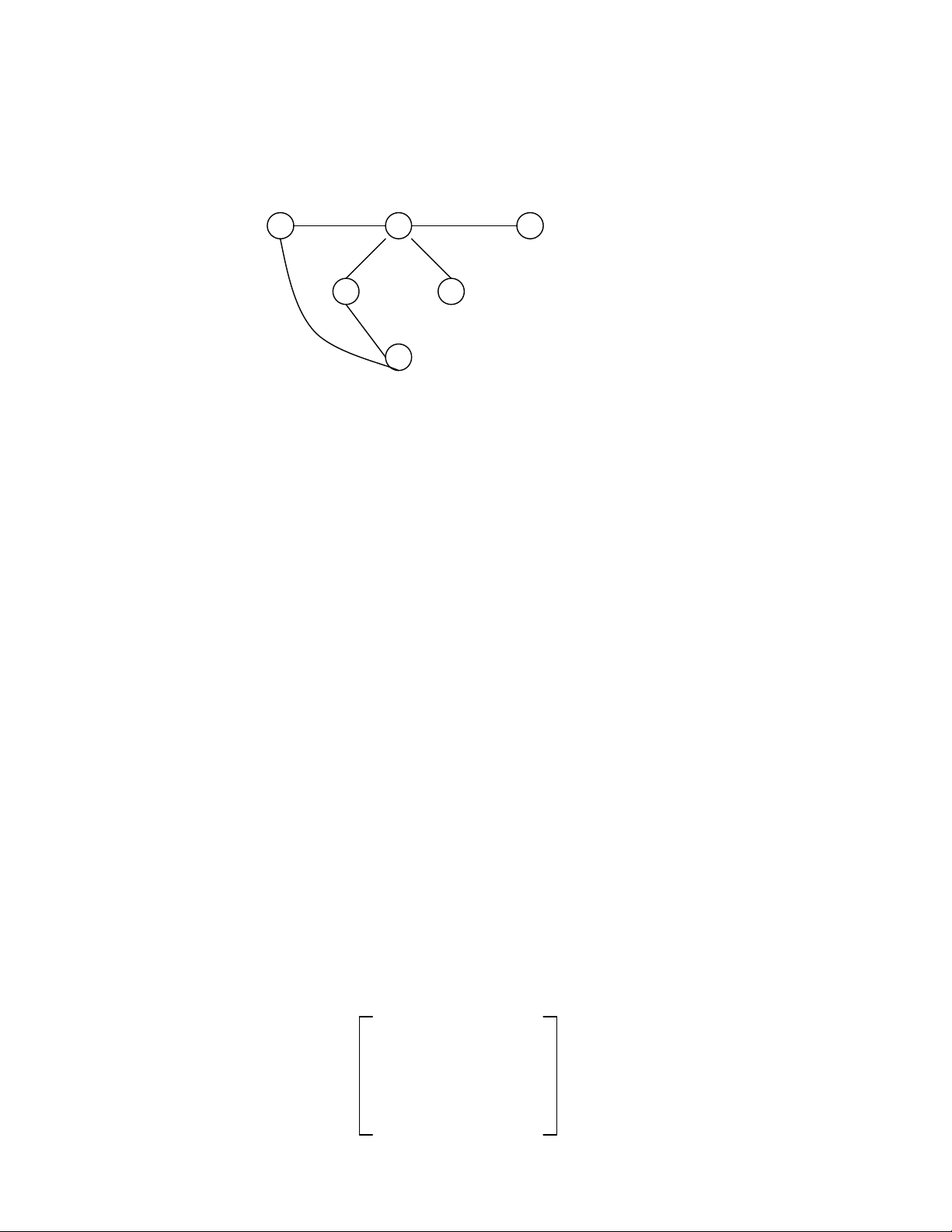
a) Đồ thị có hướng 1 1 2 3 2 3 4 5 G4 4 5 G3 b ) Đồ thị vô hướng Hình 6.1 Mộ t đường đi (path) từ đ ỉnh u tới đỉnh v là 1 dãy các đỉnh : x0, x1,…,xn-1, xn (n là số nguyên dương), trong đó : u = x0, v = xn và (xi, xi+1) với i = 0, 1, 2, …, n-1 là các cung thuộc E , u gọi là đỉnh đầu , v gọi là đỉnh cuối. Số lượng các cung trên 1 đường đi được gọ i là độ dài của đ ường đ i (path length). Mộ t đường đ i đơn (simple path) là đường đ i mà mọi đ ỉnh trên đó, trừ đ ỉnh đầu và đỉnh cuối đều khác nhau. Trường h ợp đỉnh đầu trùng với đỉnh cuố i ta gọi là chu trình (cycle). Ví dụ : với đồ th ị G2 (hình 6.1),ta có : Đường đ i 1, 2, 3, 4 là đường đi đ ơn có độ dài bằng 3. Đường đ i 1, 4, 2, 3, 1 là 1 chu trình có độ dài bằng 4. Mộ t đồ thị gọi là liên thông(cennected) nếu luôn có đường đi giữa 2 đ ỉnh bất kì của nó. Đố i với đồ thị có hướng thì trường hợp đó người ta gọ i là liên thông mạnh (strengly connected). Ví dụ : trong hình 6.1 : - Các đồ th ị G2 và G3 là liên thông. - Các đồ th ị G1 và G4 là không liên thông (vì ở G1 không có đường đi, chẳng hạn, từ đ ỉnh 1 đ ến đỉnh 2 ; ở G4 không có đường đ i từ đỉnh 4 d ến đỉnh 3 v.v…). Có khi ở mỗ i cung củ a đồ thị người ta gắn vào đấy 1 giá trị thể hiện 1 thông tin nào đó có liên quan tới cung, giá trị đó được gọ i là trọng số, và đồ thị đ ược gọ i là đồ thị có trọng số (weighted graph).
Ví dụ : đồ thị trên hình 6.2 thể hiện các đường đi nố i giữ a6 tỉnh A, B, C, D, E, F với các trọng số là độ dài tính theo km, của các tuyến đường. 83 55 A B C 60 47 D E 150 26 F Hình 6.2 II. BIỂU DIỄN TRONG MÁY CỦA ĐỒ THỊ Cũng như các cấu trúc dữ liệu nói ở các chương trước, đối với đồ th ị, ta cũng xét tới 2 cách biểu diễn thông dụng sau đ ây : 1. Biểu diễn bằ ng ma trận lân cận (lưu trữ kế tiếp) Xét 1 đồ thị có hướng G (V, E) với V có n đỉnh (n≥1). Giả sử các đ ỉnh đã được đánh số từ 1 đến n. Đồ th ị G có thể được biểu diễn trong máy bởi 1 ma trận vuông A, kích thước n × n, mà các phần tử Aij của nó sẽ nhận giá trị 1 hoặc 0 : Aij = 1 nếu trên G tồn tại 1 cung đi từ đỉnh i tới đỉnh j. Aij = 0 nếu không có cung giữa đỉnh i và j. Dĩ nhiên với đồ thị vô hướng, n ếu tồn tại 1 cung (i, j) thì ta có th ể h iểu là tồn tại 1 cung đi từ i đến j, và ngược lại, cũng tồn tại 1 cung đi từ j tới i, ngh ĩa là Aij =1thì Aji = 1. Như vậy với đồ th ị vô hướng thì ma trận A biểu diễn nó có các phân tử đố i xứng với nhau qua đường chéo chính. Ma trận A được gọi là ma trận lân cận hay ma trận kề (adjacency matrix) của đồ thị G. Ví dụ : với đồ th ị G2 ở h ình 6.1 thì ma trận lân cận có dạng 0 1 1 1 A= 0 0 1 0 1 0 0 1 0 1 0 0
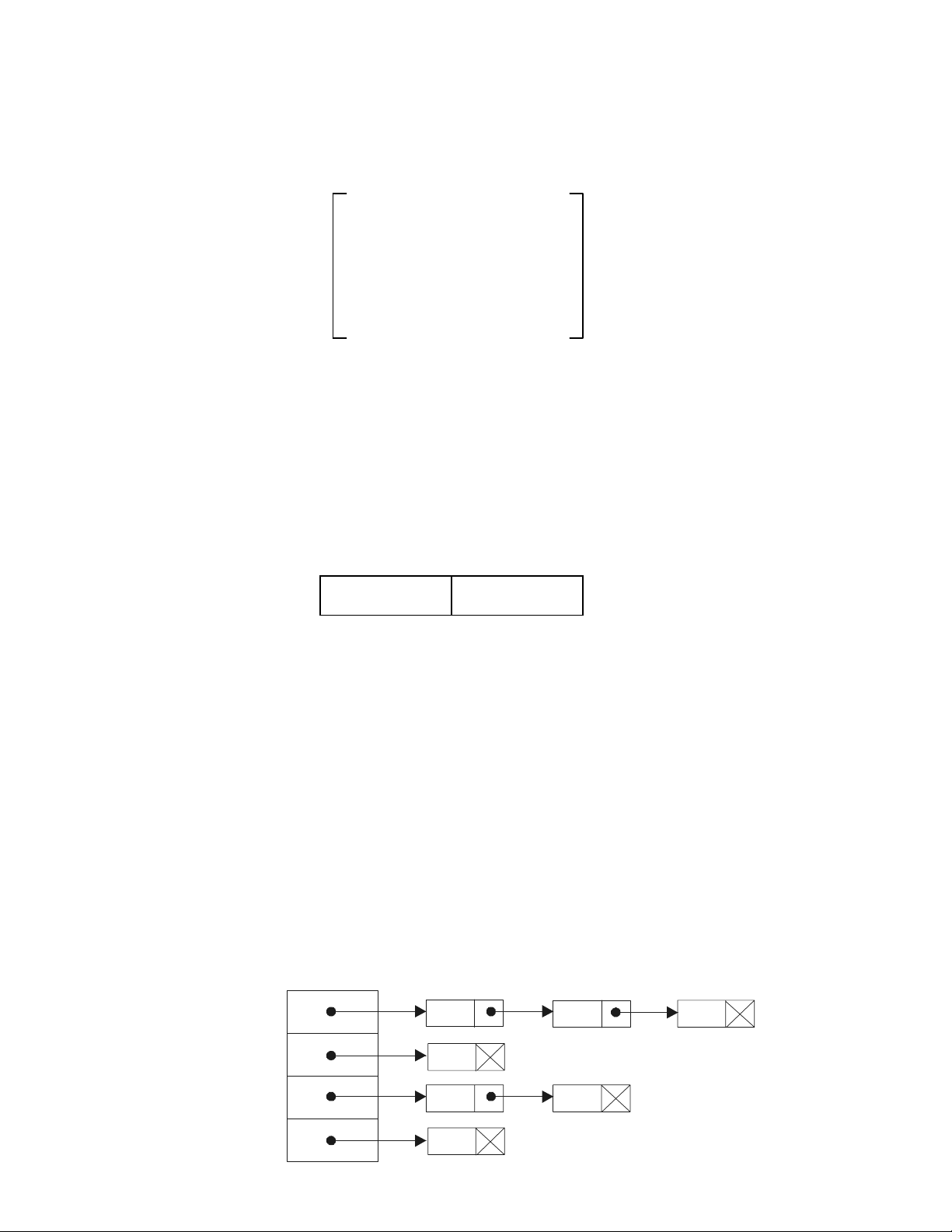
Với đồ th ị G3 ở h ình 6.1 thì ma trận lân cận có dạng : 0 1 0 1 0 1 0 1 1 0 A= 0 1 0 0 1 1 1 0 0 1 0 0 1 1 0 Do ma trận được lưu trữ kế tiếp (đã nêu ở mục 2.2.2 chương 2) nên việc truy cập vào các phần tử của ma trận lân cận được thự c hiện trực tiếp với tố c độ nhanh. Nhưng cách lưu trữ này rõ ràng tốn không gian nhớ khi n lớn. 2. Biểu diễn bằ ng danh sách lân cận (lưu trữ móc nố i) Với cách biểu diễn này mỗi đ ỉnh sẽ ứng với 1 danh sách móc nối được gọi là danh sách lân cận hay danh sách kề (adjacency list). Mỗi nút trong danh sách đó có quy cách : VERTEX LINK Trường VERTEX chứa số j ứng với đ ỉnh j là lân cận củ a đỉnh i (1≤ i ≤ n) trong danh sách lân cận củ a i. Trường LINK chứa con trỏ, trỏ tới nút tiếp theo trong danh sách. Danh sách có m nút (người ta còn gọi là “nút danh sách”) ; nếu đ ỉnh i có m đỉnh lân cận. Mỗ i danh sách như vậy lại có “nút đầu danh sách” (list head node). Thường các “ nút đầu danh sách” là các phần tử của 1 vectơ V, có kích thước bằng n, phần tử V[i] của V(1≤ i ≤ n ), ứng với danh sách lân cận của nút thứ i, nó chứa địa chỉ nút đầu tiên của danh sách lân cận này. Hình ảnh danh sách lân cận biểu diễn đồ thị G2 và G3 sẽ như sau : V[1] 2 3 4 V[2] 3 V[3] 1 4 V[4] 2
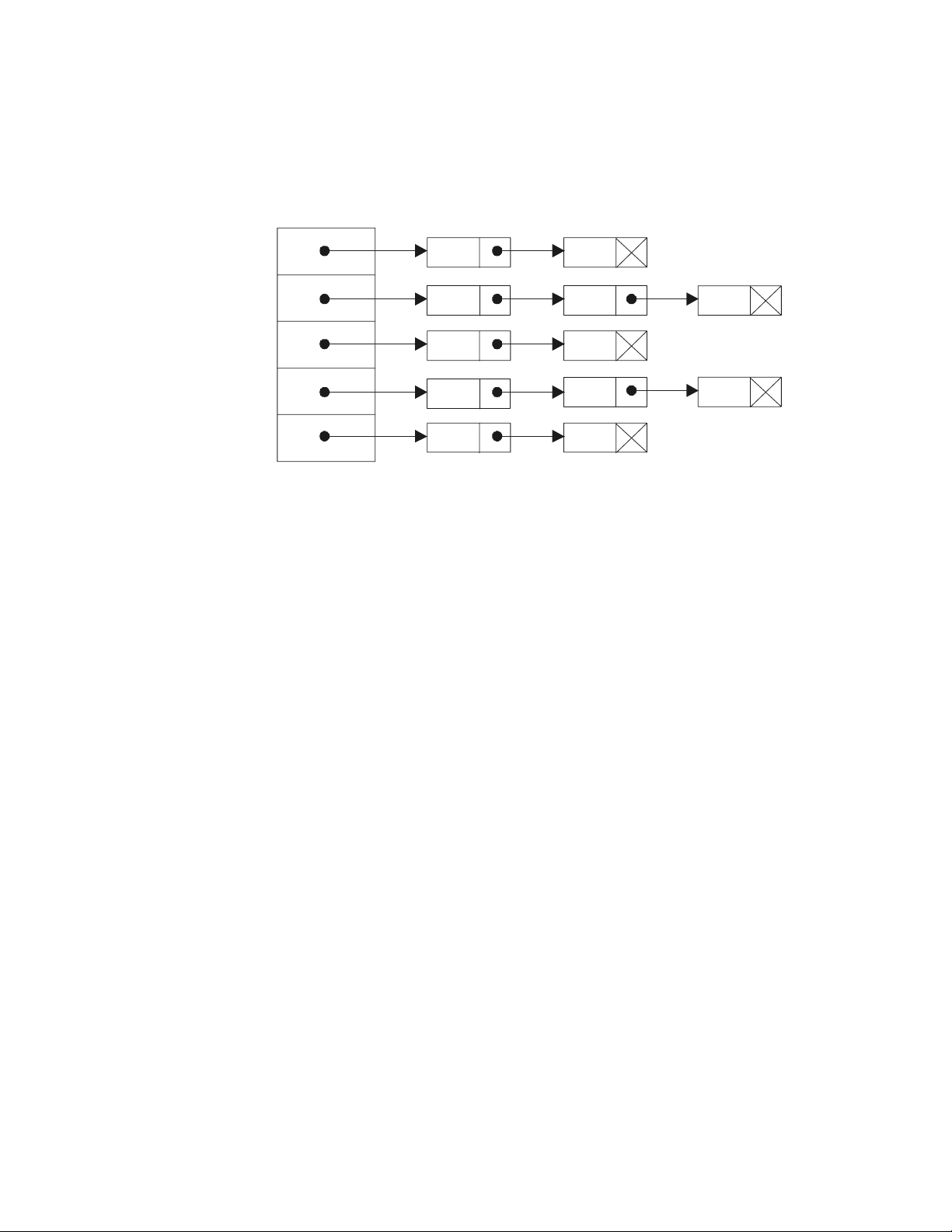
a) Danh sách lân cận biểu diễn G2 V[1] 2 4 V[2] 1 3 4 V[3] 2 5 V[4] 2 5 1 V[5] 3 4 b ) Danh sách lân cận biểu diễn G3 (ở đây ta quy ước : Các số ở trường VERTEX củ a các nút được sắp xếp theo thứ tự tăng d ần ) Hình 6.3 Ta thấy nếu đồ thị có hướng G (V, E) có n đỉnh, e cung thì số nút cần thiết sẽ là : n “nút đ ầu danh sách” và e “nút danh sách”. Nhưng với đồ thị vô hướng thì lại cần n + 2e nút. III. ÁP DỤNG 1.Bài toán đi tìm đường đi Xét 1 đồ thị G(V, E) với n đỉnh được đánh số từ 1 tới n. Mộ t câu hỏi có thể được đặt ra là : “có hay không đ ường đi từ đ ỉnh i tới đỉnh j ?”(1) Nếu đồ thị này biểu diễn 1 mạng lưới đường bộ giữa các thành phố thuộ c 1 vùng nào đó thì đố i với 1 người đi du lịch bằng xe đạp, muốn đi từ i đ ến j, câu hỏ i này họ sẽ phải đ ặt ra đầu tiên. Hành trình của họ ch ỉ có thể tiếp tụ c được nếu câu trả lời là “có”. Mà “có” thì cần phải hiểu là : có thể có nhiều đường nhưng ít nhất thì cũng phải có 1 đường. Vậy để trả lời cho câu hỏi (1) đặt ra ở trên ta phải dự a vào đâu? Ta biết rằng : đồ thị G(V, E) được biểu diễn trong máy bởi ma trận lân cận A. Nếu Aij = 1 thì nghĩa là có 1 cung đi từ i tới j hay có thể nói : có đường đ i độ dài 1 (bằng 1 cung) từ i tới j.
Nhưng ma trận A không đủ để trả lời cho câu hỏi trên, vì đường đi từ i tới j không nh ất thiết ph ải là 1 cung. Rất có thể không có cung đi từ i tới j, nhưng vẫn có đường đi từ i tới j, qua 1 số đỉnh khác. Nếu qua 1 đ ỉnh khác thì đường đi đơn sẽ có độ dài 2, nếu qua 1 đỉnh khác thì đ ường đi đ ơn có độ dài 3, v.v…Nếu đỉnh i khác đỉnh j thì đường đi đơn dài nh ất từ i tới j sẽ có độ dài (n – 1) còn nếu i trùng với j thì có th ể ta có 1 chu trình với độ d ài cực đại là n. Vì vậ y ta cần xét thêm các ma trận mới được xây d ựng từ ma trận lân cận A của G(V, E). Trước h ết ta th ấy ; các phân tử củ a ma trận A chỉ lấy giá trị là 1 hoặc 0 ( giá trị lôgích). Vì vậy ta có thể coi ma trận A là 1 ma trận lôgích. Bây giờ ta xét tới các phép toán lôgích tác động lên các ma trận lôgích. Đầu tiên ta nhắc lại 2 phép toán lôgích tác động trên các biến lôgích a và b (biến ch ỉ nh ận giá trị 0 ho ặc 1) đó là phép cộng lôgích và phép nhân lôgích. - Phép cộng lôgích (hay còn gọi là phép tuyển, phép hoặ c) được kí hiệu là ∨ (trong ngôn ngữ lập trình được gọi là OR). - Phép nhân lôgích (hay còn gọ i là phép hội, phép và) được kí hiệu là ∧ (trong ngôn ngữ lập trình được gọ i là AND).Quy tắc của chúng được nêu trong bản sau : a∨b a∧b a b 0 0 0 0 0 1 1 0 1 0 1 0 1 1 1 1 Xét 2 ma trận lôgích A và B, kích thước n × n : • Phép cộng lôgích A và B đ ể cho ma trận tổng C, kích thước n × n : C = A ∨ B, sẽ được thự c hiện bằng cách tính : Cij = Aij ∨ Bij với 1≤ i ≤ n 1≤ j ≤ n • Phép nhân lôgích A và B đ ể cho ma trận tích D kích thước n × n : D = A ∧ B, sẽ được thực hiện bằng cách tính : (Aik ∧ Bkj) với 1≤ i ≤ n Dij = 1 ≤ j ≤ n. Với ma trận lân cận A của G đã biết, ta có : A(2) = A ∧ A. Ta thấy phần tử Aij(2) của A(2) bằng 1 khi và chỉ khi, ít nh ất có 1 giá trị k đ ể
n Aik ∧ Akj = 1 (Aij(2) = V (Aik ∧ Bkj) mà Aik ∧ Bkj = 1 khi và chỉ khi có Aik = 1 k =1 và Akj = 1; ngh ĩa là có 1 cung đi từ i tới k và có 1 cung đi từ k tới j. Điều đó ch ứng tỏ : có 1 đường đi độ d ài 2 từ i tới. Như vậy ma trận A(2) sẽ cho ta câu trả lời của câu hỏi : “có hay không đường đi độ dài 2 từ i tới j” : Nếu Aij(2) = 1 thì nghĩa là “có”. Nếu Aij(2) = 0 thì nghĩa là “không”. Tương tự như vậy ta có thể xét tới các ma trận : A(3) = A ∧ A(2) ; A(4) = A ∧ A(3) ; … A = A ∧ A(r-1) (r) và ta cũng suy ra đ ược : Nếu Aij(r ) = 1 thì “có” đường đi độ dài r từ i tới j (ít nh ất cũng có 1 đường). Nếu Aij(r ) = 0 thì “không có”. Từ đó ta th ấy rằng : để trả lời cho câu hỏi (1) đặt ra ở trên ta ph ải lập ma trận : P = A ∨ A(2) ∨ A(3) ∨ … ∨ A(n) (2) n = V A(k) k =1 và n ếu : Pij = 1 thì câu trả lời là “có” Pij = 0 thì câu trả lời là “không”. Ma trận P đ ược gọ i là ma trận đường đi (path matrix) củ a G. Việc tính P theo công thức (2) sẽ tốn nhiều th ời gian khi n lớn. Giải thuật của warshall nêu sau đ ây, có hiệu lực cao hơn. Void WARSHALL (A, n, P) ; { for (i=1;i
Ví dụ : Cho đồ thị G với ma trận lân cận A có dạng như sau : 0 0 1 1 0 1 2 0 1 0 1 0 1 0 0 0 0 A= 0 0 0 0 1 3 0 0 1 0 0 3 4 Hình 6.4 2 Ta xét việc tính A(2) . Biết rằng mỗi phân tử được tính theo công th ức : A ij 5 Aij = V (Aik∧Ajk) với 1 ≤ i, j≤ 5. Chẳng hạn : 2 k =1 = A11 ∧ A11 ∧ A12 ∧ A21 ∧ A13 ∧ A31 ∧ A14 ∧ A41∧ A15 ∧ A51 2 A 11 = 0 ∧ 0 ∨ 1 ∧ 0 ∨ 0 ∧1 ∧1 ∨ 0 ∧ 0 ∨ 0 ∧ = 0 A12 = 0 ∧ 1 ∨ 1 ∧ 0 ∨ 0 ∧0 ∧1 ∨ 0 ∧ 0 ∨ 1 ∧ = 0… 2 cuối cùng, ta có ; 0 0 1 1 1 1 0 0 0 1 A(2)= 0 1 0 1 0 = 0 1 0 0 0 0 0 1 1 0 Tương tự ta cũng tính được : 0 1 1 1 0 1 0 1 0 1 0 0 1 1 1 A(3)= 1 0 0 1 0 A(4)= 1 0 1 1 0 0 1 0 1 1 = 1 0 0 0 1 = 0 1 0 1 0 0 1 0 1 0 0 0 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1 1 0 A(6)= 1 1 1 1 1 A(5)= 1 1 0 0 1 1 1 = 1 1 1 1 1 0 0 0 = 1 1 1 1 1 0 1 1 0 1
Từ kết qu ả trên có thể nêu lên 1 số nhận xét, ví dụ : A(2)[1,5] = 1 ngh ĩa là : có đường đi độ dài 2 từ 1 tới 5 (không có cung từ 1 tới 5). Kiểm tra trên đồ thị ta thấy đó chính là đường đi 1, 4, 5. (3) A [4, 3] = 1 nghĩa là : có đ ường đi độ dài 3 từ 4 tới 3. Đó chính là đường đ i 4, 5, 2, 3. A(4)[3, 2] = 1 nghĩa là có đường đi độ dài 4 từ 3 đ ến 2. Đó chính là đường đ i 3, 1, 4, 5, 2. A(5)[5, 5] = 1 nghĩa là : có chu trình độ dài 5, tại đỉnh 5. Đó chính là chu trình 5, 2, 3, 1, 4, 5. Các phân tử củ a P đều b ằng 1 chứng tỏ từ bất kì 1 đỉnh nào trên đồ thị G cũng có đường đ i tới 1 đ ỉnh khác. Nói 1 cách khác G là đồ thị liên thông mạnh. Hơn nữa : bất kì đỉnh nào trên đồ thị G cũng là đỉnh đ ầu và đỉnh cuối củ a ít nh ất 1 chu trình. 2. Bài toán sắp xếp Tô – pô Ta hãy xét 1 bài toán cụ thể : Có n công việc ; giả sử, để phân biệt, ta đánh số từ 1 đến n. Giữa các công việc này có 1 quan hệ mà ta gọi là quan hệ “làm trước” và kí hiệu bởi d ấu
8, 7, 2, 4, 5, 3, 6, 1, (3) Ho ặ c 7, 8, 2, 4, 3, 5, 6, 1, (4) thì việc thực hiện sẽ hoàn toàn thu ận lợi vì nếu theo (3): - Khi công việc 2 được thự c hiện thì các công việc cần phải làm trước như công việc 7, công việc 8 đã dược thực hiện rồ i - Khi công việc 4 thực hiện thì công việc 2 đã được thực hiện rồ i - Khi công việc 3 được th ực hiện thì công việc 2 và 4 đã được thực hiện rồi - Khi công việc 5 thực hiện thì công việc 4 đã được thực hiện rồ i - Khi công việc 6 thực hiện thì công việc 3 và 5 đ ã được thực hiện rồi Mộ t thứ tự như (3) ho ặc (4), được gọi là thứ tự Topo (Topological order), việc sắp xếp như trên gọi là sắp xếp Topo (Topological sort). Ta cũng th ấy: Các công việc với quan h ệ “làm trước”, kí hiệu bằng
Như vậy sắp xếp Topo đ ối với tập các công việc này chính là sắp xếp các đỉnh của đồ th ị nói trên thành một dãy theo hàng ngang sao cho các cung (mũ i tên) đ ều hướng từ trái sang phải . Có thể thực hiện được đ iều này bằng qui tắ c chung như sau: - Đầu tiên chọn ra một đỉnh không có cung nào đ i tới nó (không có mũ i tên đâm vào nó) và đưa đỉnh đó ra sắp xếp - Lo ại đ ỉnh này ra kh ỏi đồ th ị cùng với các cung xuất phát từ nó. Vì nó đ ã trở thành “trước” của các đỉnh lân cận củ a nó rồ i nên cung thể h ịên quan hệ n ày không cần nữa - Đồ th ị với các đỉnh còn lại, lại đ ược thực hiện tương tự như trên và cứ như th ế cho tới khi các đ ỉnh đã được đưa ra sắp xếp theo thứ tự tuyến tính Trường h ợp cùng một lúc nếu có nhiều đ ỉnh đều không có cung nào đi tới nó thì có thể chọn một đ ỉnh tu ỳ ý. Như vậy nghĩa là: có thể có nhiều th ứ tự Topo khác nhau. Có thể diễn tả quá trình thực hiện “qui tắc sắp xếp Topo” nêu trên, với đồ th ị hình 6.5 như hình 6.6 Đỉnh đưa ra sắp xếp Phần đồ thị còn lại
2 3 4 1 7 8 5 6 8 1 2 3 4 5 6 1 3 4 2 6 5 1 3 4 5 6 1 3 6 5 5 1 6 1 6 1 Hình 6.6 Tho ạt đ ầu ta thấy đ ỉnh 7 và 8 đều không có cung nào đi tới nó. Giả sử ta chọn 7 để đưa ra sắp xếp trước tiên.
Như vậy ta đã có một thứ tự Topo giống nh ư dãy (4) đã nêu ở trên. Bây giờ đồ thị với các đỉnh được sắp xếp theo thứ tự tuyến tính, sẽ có dạng như h ình 6.7 7 8 2 4 3 5 6 1 Hình 6.7 Rõ ràng: ở đây các cung đ i từ trái sang ph ải nghĩa là theo thứ tự tuyến tính này thì th ứ tự bộ phận đã được đ ảm bảo, hay nói mộ t cách khác khi thực hiện tu ần tự các công việc như trên việc nào cần làm trước đều đã được làm trước. Việc xây dựng một giải thuật sắp xếp Topo sẽ đòi hỏi ta phải biết được: - Số các cung đi tới một đỉnh. Nếu số này bằng 0 thì đ ỉnh dó có th ể đư a ra săp xếp được. - Các cung đ i ra từ một đ ỉnh i, ngh ĩa là biết các đỉnh lân cận của i. Để khi một đỉnh i nào đó đã được đưa ra sắp xếp thì số lượng cung đi vào đỉnh lân cận j của nó sẽ được giảm đi 1 (ứng với việc loại cung xuất phát từ đỉnh i). Các yêu cầu này sẽ đ ược thoã mãn nếu ta cài đặt đồ thị bằng danh sách lân cận , với qui ước b ổ sung như sau: Nút “đầu danh sách” của danh sách lân cận ứng với đỉnh i, ngoài trường LINK, như thông thường còn có thêm trường COUNT mà COUNT (i) ghi nh ận số các cung đi tới đỉnh i. Như với đồ th ị hình 6.5 thì cấu trúc lưu trữ của nó có dạng như h ình 6.8 Dĩ nhiên phải có một chương trình tạo lập nên có cấu trúc này ở trong máy, trước khi thực hiện sắp xếp Topo Giải thuật Topo – order sau đây sẽ th ực hiện sắp xếp Topo cho tập S có thứ tự bộ ph ận với S đ ược biễu diễn bởi đồ th ị mà cấu trúc lưu trữ của nó có dạng danh sách lân cận như vừa nêu ở trên. Trong giải thuật này COUNT LINK người ta dùng một queue Q để lưu trữ các đỉnh i mà 1 COUNT (i) = 0 V[1] 2 V[2] 3 4 2 V[3] 6 1 V[4] 3 5 1 V[5] 6 2 V[6] 1 0 V[7] 2 0 V[8] 2 Hình 6.8
Void TOPO-ORDER(COUNT,VERTEX,LINK,n) { For (i=1;i