
CH NG 6ƯƠ
BÀI TOÁN Đ NG ĐI NG N NH TƯỜ Ắ Ấ
1. Các khái ni m ệ
Trong ch ng này chúng ta ch xét đ th có h ng G =(V,E), |V|=n, |E|=m v i các cung đ cươ ỉ ồ ị ướ ớ ượ
gán tr ng s , nghĩa là, m i cung (u,v) ọ ố ỗ
∈
E c a nó đ c đ t t ng ng v i m t s th c a(u,v)ủ ượ ặ ươ ứ ớ ộ ố ự
g i là tr ng s c a nó. Chúng ta s đ t a(u,v) = ọ ọ ố ủ ẽ ặ
∞
, n u (u,v) ế
∉
E.
N u dãy vế0, v1, . . ., vp là m t đ ng đi trên G, thì đ dài đ ng đi là t ng c a các tr ng s trênộ ườ ộ ườ ổ ủ ọ ố
các cung c a nó:ủ
∑
=−
p
i
ii
vva
1
1
),(
(n u gán tr ng s cho t t c cung b ng 1, thì đ dài c a đ ng đi là s cung c a đ ng đi.)ế ọ ố ấ ả ằ ộ ủ ườ ố ủ ườ
Đ ng đi ng n nh t t đ nh s đ n đ nh t là đ ng đi có đ dài nh nh t t s đ n t, đ dài c aườ ắ ấ ừ ỉ ế ỉ ườ ộ ỏ ấ ừ ế ộ ủ
nó ký hi u là d(s,t). d(s,t) còn g i là kho ng cách t s đ n t. N u không có đ ng đi t s đ n tệ ọ ả ừ ế ế ườ ừ ế
thì ta s đ t d(s,t)=ẽ ặ
∞
.
N u bi t kho ng cách t s đ n t, thì đ ng đi ng n nh t t s đ n t, trong tr ng h p tr ng sế ế ả ừ ế ườ ắ ấ ừ ế ườ ợ ọ ố
không âm, có th tìm đ c m t cách d dàng. Đ tìm đ ng đi, ch c n đ ý là đ i v i c pể ượ ộ ễ ể ườ ỉ ầ ể ố ớ ặ
đ nh s, t ỉ
∈
V tuỳ ý (s
≠
t) luôn tìm đ c đ nh v sao choượ ỉ
d(s,t) = d(s,v) + a(v,t).
Th c v y, đ nh v nh v y chính là đ nh đi tr c đ nh t trong đ ng đi ng n nh t t s đ n t.ự ậ ỉ ư ậ ỉ ướ ỉ ườ ắ ấ ừ ế
Ti p theo ta l i có th tìm đ c đ nh u sao cho d(s,v) = d(s,u) + a(u,v), . . . T đó ta có thu tế ạ ể ượ ỉ ừ ậ
toán sau đây đ tìm đ ng đi ng n nh t t s đ n t khi bi t đ dài c a nó.ể ườ ắ ấ ừ ế ế ộ ủ
void Find_Path()
/*
Đ u vào:ầ
d[v] là kho ng cách t đ nh s đ n đ nh vả ừ ỉ ế ỉ
∈
V; t là đ nh đích;ỉ
a[u,v], u, v
∈
V là ma tr n tr ng s trên các cung. ậ ọ ố
Đ u ra:ầ
M ng stack ch a dãy đ nh xác đ nh đ ng đi ng n nh t t s đ n tả ứ ỉ ị ườ ắ ấ ừ ế
*/
{
stack=
φ
; stack
⇐
t; v=t;
while (v != s)
{
u=đ nh tho mãn d[v]=d[u]+a[u,v];ỉ ả
stack
⇐
u;
v=u;
}
}
Nh n xét:ậ
-Đ ph c t p tính toán c a thu t toán là O(nộ ứ ạ ủ ậ 2), do đ tìm đ nh u ta ph i xét qua t t c cácể ỉ ả ấ ả
đ nh c a đ th . ỉ ủ ồ ị
1

-Có th dùng bi n m ng Truoc[v], đ ghi nh đ nh đi tr c v trong đ ng đi tìm ki m (khongể ế ả ể ớ ỉ ướ ườ ế
dùng m ng stack)ả
2. Đ ng đi ng n nh t xu t phát t m t đ nhườ ắ ấ ấ ừ ộ ỉ
Ph n l n các thu t toán tìm kho ng cách gi a hai đ nh s và t đ c xây d ng nh sau: ầ ớ ậ ả ữ ỉ ượ ự ư
Tính c n trên d[v] c a kho ng cách t s đ n t t c các đ nh v ậ ủ ả ừ ế ấ ả ỉ
∈
V. M i khi phát hi n ỗ ệ
d[u] + a[u,v] < d[v] (1)
c n trên d[v] s đ c làm t t lên v i giá tr m i: d[v]= d[u] + a[u,v].ậ ẽ ượ ố ớ ị ớ
Quá trình đó s k t thúc khi không làm t t thêm đ c b t kỳ c n trên nào. Khi đó, rõ ràng giáẽ ế ố ượ ấ ậ
tr c a m i d[v] s cho kho ng cách t đ nh s đ n đ nh v. C n trên d[v] s đ c g i là nhãnị ủ ỗ ẽ ả ừ ỉ ế ỉ ậ ẽ ượ ọ
c a đ nh v, còn vi c tính l i các c n này s đ c g i là th t c gán nhãn. ủ ỉ ệ ạ ậ ẽ ượ ọ ủ ụ
Nh n th y r ng đ tính kho ng cách t s đ n t, đây, ta ph i tính kho ng cách t s đ n t tậ ấ ằ ể ả ừ ế ở ả ả ừ ế ấ
c các đ nh còn l i c a đ th . Hi n nay v n ch a bi t thu t toán nào cho phép tìm đ ng điả ỉ ạ ủ ồ ị ệ ẫ ư ế ậ ườ
ng n nh t gi a hai đ nh làm vi c th c s hi u qu h n nh ng thu t toán tìm đ ng đi ng nắ ấ ữ ỉ ệ ự ự ệ ả ơ ữ ậ ườ ắ
nh t t m t đ nh đ n t t c các đ nh còn l i.ấ ừ ộ ỉ ế ấ ả ỉ ạ
S đ tính toán mà ta v a mô t còn ch a xác đ nh, b i vì còn ph i ch ra th t các đ nh u vàơ ồ ừ ả ư ị ở ả ỉ ứ ự ỉ
v đ ki m tra đi u ki n (1). Th t ch n này có nh h ng r t l n đ n hi u qu c a thu tể ể ề ệ ứ ự ọ ả ưở ấ ớ ế ệ ả ủ ậ
toán.
Bây gi ta s mô t thuât toán Ford-Bellman tìm đ ng đi ng n nh t t đ nh s đ n t t c cácờ ẽ ả ườ ắ ấ ừ ỉ ế ấ ả
đ nh còn l i c a đ th . Thu t toán làm vi c trong tr ng h p tr ng s c a các cung là tuỳ ý,ỉ ạ ủ ồ ị ậ ệ ườ ợ ọ ố ủ
nh ng gi thi t r ng trong đ th không có chu trình âm. ư ả ế ằ ồ ị
void Ford_Bellman()
/*
Đ u vào: ầ
Đ th có h ng G=(V,E) v i n đ nh, ồ ị ướ ớ ỉ
s là đ nh xu t phát, a[u,v] là ma tr n tr ng s ;ỉ ấ ậ ọ ố
Gi thi t: Đ th không có chu trình âm.ả ế ồ ị
Đ u ra:ầ
Kho ng cách t đ nh s đ n t t c các đ nh còn l i d[v] ả ừ ỉ ế ấ ả ỉ ạ
Tr c[v] ghi nh n đ nh đi tr c v trong đ ng đi ng n nh t t s đ n v.ướ ậ ỉ ướ ườ ắ ấ ừ ế
*/
{
// Kh i t o ở ạ
for (v
∈
V)
{
d[v]=a[s,v];
Truoc[v]=s;
}
d[s]=0;
//cac lenh lap
for (k=1;k<= n-2;k++)
for (v
∈
V\{s})
2
for (u
∈
V)
if (d[v] > d[u] +a[u,v])
{
d[v]=d[u]+a[u,v];
Truoc[v]=u;
}
}
Tính đúng đ n c a thu t toán có th ch ng minh trên c s trên nguyên lý t i u c a quyắ ủ ậ ể ứ ơ ở ố ư ủ
ho ch đ ng. Rõ ràng là đ ph c t p tính toán c a thu t toán là O(nạ ộ ộ ứ ạ ủ ậ 3). L u ý r ng chúng ta cóư ằ
th ch m d t vòng l p theo k khi phát hi n trong quá trình th c hi n hai vòng l p trong khôngể ấ ứ ặ ệ ự ệ ặ
có bi n d[v] nào b đ i giá tr . Vi c này có th x y ra đ i v i k<n-2, và đi u đó làm tăng hi uế ị ổ ị ệ ể ả ố ớ ề ệ
qu c a thu t toán trong vi c gi i các bài toán th c t . Tuy nhiên, c i ti n đó không th c sả ủ ậ ệ ả ự ế ả ế ự ự
c i thi n đ c đánh giá đ ph c t p c a b n thân thu t toán. Đ i v i đ th th a t t h n là sả ệ ượ ộ ứ ạ ủ ả ậ ố ớ ồ ị ư ố ơ ử
d ng danh sách k Ke(v), vv V, đ bi u di n đ th , khi đó vòng l p theo u c n vi t l i d iụ ề ể ể ễ ồ ị ặ ầ ế ạ ướ
d ngạ
For u v
If d[v] > d[u] + a[u,v] then
Begin
D[v]:=d[u]+a[u,v];
Truoc[v]:=u;
End;
Trong tr ng h p này ta thu đ c thu t toán v i đ ph c t p O(n,m).ườ ợ ượ ậ ớ ộ ứ ạ
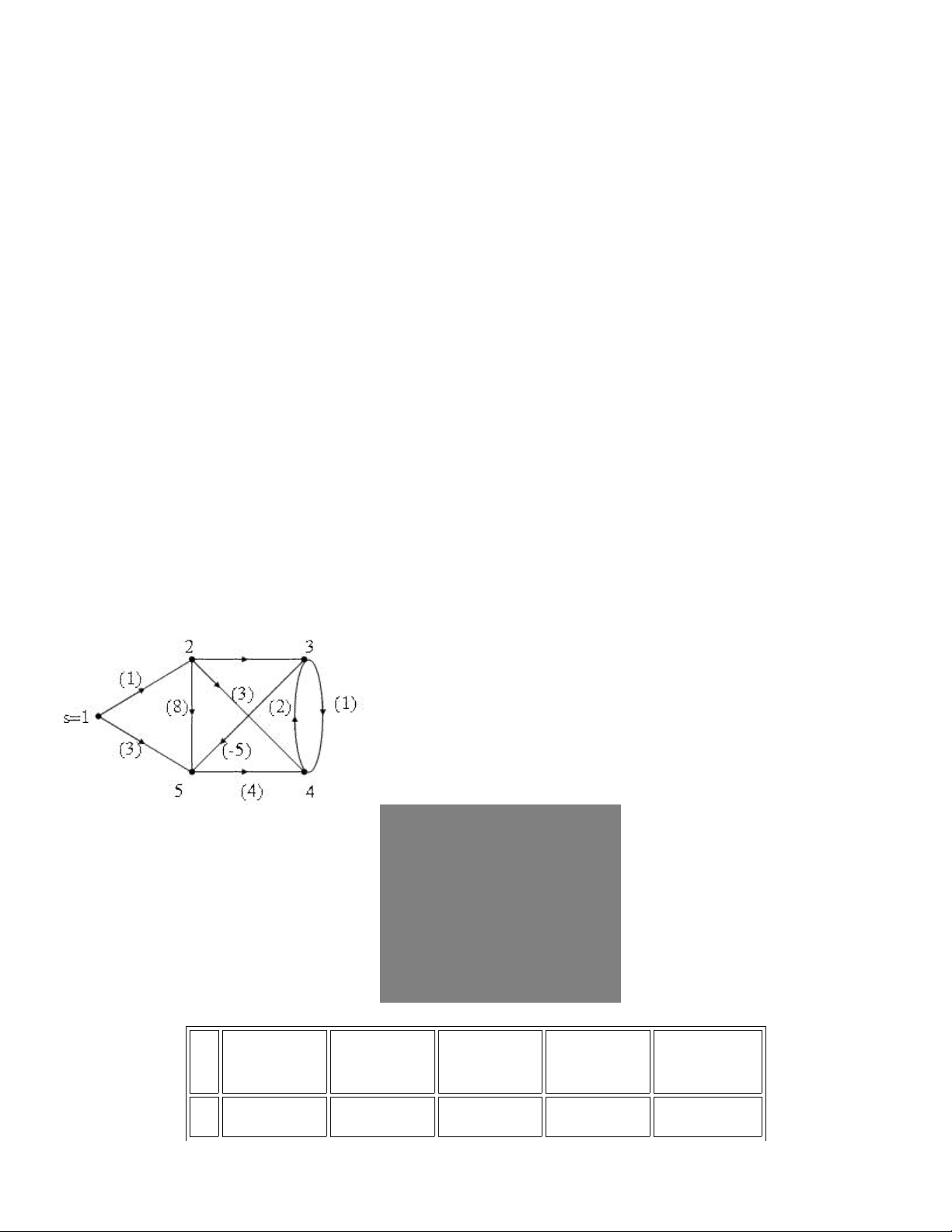
Thí d 1. xét đ th trong hình 1. Các k t qu tính toán theo thu t toán đ c mô t trong b ngụ ồ ị ế ả ậ ượ ả ả
d i đâyướ
2 2 2 2
3 3 8
A= = = = 1 -5
4 4
Hình 1. Minh h a thu t toán Ford_Bellmanọ ậ
k d[1]
Truoc[1]
d[2]
Truoc[2]
d[3]
Truoc[3]
d[4]
Truoc[4]
d[5]
Truoc[5]
0,1 1,1 1 ,1 1 ,1 3,1
3

1 0,1 1,1 4,2 4,2 -1,3
2 0,1 1,1 4,2 3,5 -1,3
3 0,1 1,1 4,2 3,5 S
B ng k t qu tính toán theo thu t toán Ford_Bellmanả ế ả ậ
Trong các m c ti p theo chúng ta s xét m t s tr ng h p riêng c a bài toán tìm đ ng điụ ế ẽ ộ ố ườ ợ ủ ườ
ng n nh t mà đ gi i chúng có th xây d ng nh ng thu t toán hi u qu h n thu t toánắ ấ ể ả ể ự ữ ậ ệ ả ơ ậ
Ford_Bellman. Đó là khi tr ng s c a t t c các cung là các s không âm ho c là khi đ thọ ố ủ ấ ả ố ặ ồ ị
không có chu trình.
3. TR NG H P MA TR N TR NG S KHÔNG ÂM - THU T TOÁN DIJKSTRAƯỜ Ợ Ậ Ọ Ố Ậ
Trong tr ng h p tr ng s trên các cung là không âm thu t toán do Dijkstra đ ngh làm vi cườ ợ ọ ố ậ ề ị ệ
h u hi u h n r t nhi u so v i thu t toán trình bày trong m c tr c. Thu t toán đ c xây d ngữ ệ ơ ấ ề ớ ậ ụ ướ ậ ượ ự
d a trên c s gán cho các đ nh các nhãn t m th i. Nhãn c a m i đ nh cho bi t c n c a đự ơ ở ỉ ạ ờ ủ ỗ ỉ ế ậ ủ ộ
dài đ ng đi ng n nh t t s đ n nó. Các nhãn này s đ c bi n đ i theo m t th t c l p, màườ ắ ấ ừ ế ẽ ượ ế ổ ộ ủ ụ ặ
m i b c l p có m t nhãn t m th i tr thành nhãn c đ nh. N u nhãn c a m t đ nh nào đóở ỗ ướ ặ ộ ạ ờ ở ố ị ế ủ ộ ỉ
tr thành m t nhãn c đ nh thì nó s cho ta không ph i là c n trên mà là đ dài c a đ ng điở ộ ố ị ẽ ả ậ ộ ủ ườ
ng n nh t t đ nh s đ n nó. Thu t toán đ c mô t c th nh sau.ắ ấ ừ ỉ ế ậ ượ ả ụ ể ư
Procedure Dijstra;
(*
Đ u vào:ầ
Đ th có h ng G=(v,E) v i n đ nh,ồ ị ướ ớ ỉ
s V là đ nh xu t phát, a[u,v], u,v V, ma trr n tr ng s ;ỉ ấ ậọ ố
Gi thi t: a[u,v]≥0, u,v V.ả ế
Đ u ra:ầ
Kho ng cách t đ nh s đ n t t c các đ nh còn l i d[v], v V.ả ừ ỉ ế ấ ả ỉ ạ
Truoc[v], v V, ghi nh n đ nh đi tr c v trong đ ng đi ng nậ ỉ ướ ườ ắ
nh t t s đ n v ấ ừ ế
*)
Begin
(* Kh i t o *)ở ạ
for v u V do
begin
d[v]:=a[s,v];
Truoc[v]:=s;
end;
d[s]:=0; T:=V\\ ss ; (* T là tt p các đ nh cá nhãn t m th i *)ậỉ ạ ờ
(* B c l p *)ướ ặ
while T <> ; do
begin
tìm đ nh u T tho mãn d[u]=minn d[z]:z TT ;ỉ ả
T:=T\\ uu ; (* CC đ nh nhãn c a đ nh u*)ốị ủ ỉ
For v T do
4
If d[v]>d[u]+a[u,v] then
Begin
d[v]:=d[u]+a[u,v];
Truoc[v]:=u;
End;
end;
End;
Đ nh lý 1. Thu t toán Dijkstra tìm đ c đ ng đi ng n nh t trên đ th sau th i gian c O(nị ậ ượ ườ ắ ấ ồ ị ờ ỡ 2).
Ch ng minh. ứ
Tr c h t ta ch ng minh là thu t toán tìm đ c đ ng đi ng n nh t t đ nh s đ n các đ nhướ ế ứ ậ ượ ườ ắ ấ ừ ỉ ế ỉ
còn l i c a đ th . Gi s m t b c l p nào đó các nhãn c đ nh cho ta đ dài các đ ng điạ ủ ồ ị ả ử ở ộ ướ ặ ố ị ộ ườ
ng n nh t t s đ n các đ nh có nhãn c đ nh, ta s ch ng minh r ng l n g p ti p theo n uắ ấ ừ ế ỉ ố ị ẽ ứ ằ ở ầ ặ ế ế
đ nh u* thu đ c nhãn c đ nh d(u*) chính là đ dài đ ng đi ng n nh t t s đ n u*.ỉ ượ ố ị ộ ườ ẵ ấ ừ ế
Ký hi u Sệ1 là t p h p các đ nh có nhãn c đ nh còn Sậ ợ ỉ ố ị 2 là t p các đ nh có nhãn t m th i b cậ ỉ ạ ờ ở ướ
l p đang xét. K t thúc m i b c l p nhãn t m th i d(uặ ế ỗ ướ ặ ạ ờ *) cho ta đ dài c a đ ng đi ng n nh tộ ủ ườ ắ ấ
t s đ n u* không n m tr ng trong t p Sừ ế ằ ọ ậ 1, t c là nó đi qua ít nh t m t đ nh c a t p Sứ ấ ộ ỉ ủ ậ 2. G i z ọ
S2 là đ nh đ u tiên nh v y trên đ ng đi này. Do tr ng s trên các cung là không âm, nênỉ ầ ư ậ ườ ọ ố
đo n đ ng t z đ n u* có đ dài L>0 và ạ ườ ừ ế ộ
d(z) < d(u*) – L < d(u*).
B t đ ng th c này là mâu thu n v i cách xác đ nh đ nh u* là đ nh có nhãn t m th i nh nh t.ấ ẳ ứ ẫ ớ ị ỉ ỉ ạ ờ ỏ ấ
V y đ ng đi ng n nh t t s đ n u* ph i n m tr n trong Sậ ườ ắ ấ ừ ế ả ằ ọ 1, và vì th , d[u*] là đ dài c a nó.ế ộ ủ
Do l n l p đ u tiên Sở ầ ặ ầ 1 = ss và sau mmi l n l p ta ch thêm vào m t đ nh u* nên gi thi tỗầ ặ ỉ ộ ỉ ả ế
là d(v) cho đ dài đ ng đi ng n nh t t s đ n v v i m i v Sộ ườ ắ ấ ừ ế ớ ọ 1 là đúng v i b c l p đ u tiên.ớ ướ ặ ầ
Theo qui n p suy ra thu t toán cho ta đ ng đi ng n nh t t s đ n m i đ nh c a đ th .ạ ậ ườ ắ ấ ừ ế ọ ỉ ủ ồ ị
Bây gi ta s đánh giá s phép toán c n th c hi n theo thu t toán. û m i b c l p đ tìm raờ ẽ ố ầ ự ệ ậ Ơ ỗ ướ ặ ể
đ nh u c n ph i th c hi n O(n) phép toán, và đ gán nhãn l i cũng c n th c hi n m t sỉ ầ ả ự ệ ể ạ ầ ự ệ ộ ố
l ng phép toán cũng là O(n). thu t toán ph i th c hi n n-1 b c l p, vì v y th i gian tínhượ ậ ả ự ệ ướ ặ ậ ờ
toán c a thu n toán c O(nủ ậ ỡ 2).
Đ nh lý đ c ch ng minh.ị ượ ứ
Khi tìm đ c đ dài c a đ ng đi ng n nh t d[v] thì đ ng đi này có th tìm d a vào nhãnượ ộ ủ ườ ắ ấ ườ ể ự
Truoc[v], vv V, theo qui t c gi ng nh chúng ta đã xét trong ch ng 3.ắ ố ư ươ
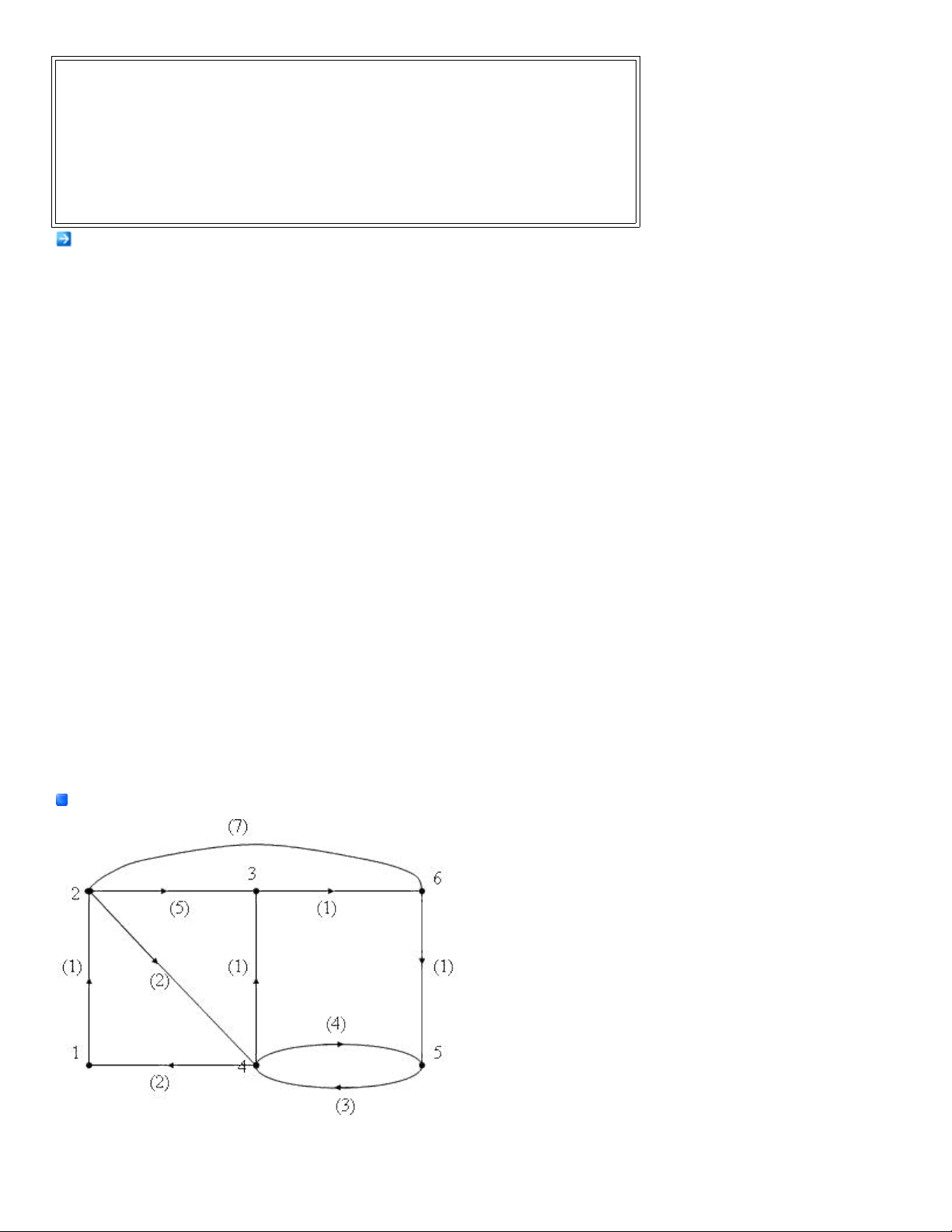
Thí d 2. Tìm đ ng đi ng n nh t t 1 đ n các đ nh còn l i c a đ th hình 2.ụ ườ ắ ấ ừ ế ỉ ạ ủ ồ ị ở
Hình 2. Minh h a thu t toán Dijkstraọ ậ
5


























