CHƯƠNG II : HÀM SỐ BẬC NHẤT VÀ HÀM SỐ BẬC HAI
§1 HÀM SỐ
Số tiết: 2
1. Mục tiêu
1.1 Về kiến thức
- Hiểu khái niệm hàm số, tập xác định của hàm số, đồ thị của hàm số.
- Hiểu hàm số động biến, nghịch biến, hàm số chẵn , lẻ. Biết được tính đối xứng của đồ thị hàm
số chẵn, đồ thị hàm số lẻ.
1.1. Về kĩ năng
- Biết tìm tập xác định của hàm số đơn giản.
- Biết chứng minh tính đồng biến, nghịch biến của một hàm số trên một khoảng cho trước.
- Biết xét tính chẳn, lẻ của một hàm số đơn giản.
2. Chuẩn bị phương tiện dạy học:
- GV: Soạn giáo án, SGK
- HS: đã biết đn HS ở cấp II
3. Tiến trình bài học và các hoạt động
TIẾT 1
Hoạt động 1: Hàm số . tập xác định của hàm số
Hoạt động 2: Cách cho hàm số bằng bảng
HĐ của GV HĐ của HS Nội dung
Ví dụ 1: cho y = x- 1.
Tìm y khi x = 1, x = -1, x
= 2. Với mỗi giá trị x ta
tìm được bao nhiêu giá trị
y
Ví dụ 2 (VD1. SGK)
Hãy nêu một ví dụ thực tế
về hàm số
- Cho biết kết quả
x -1 1 ……
y ? ? ……
- Từ kiến thức lớp 7 & 9 hs
hình thành khái niệm hàm số.
- Học sinh cho
- HS nhận xét
- Chỉnh sửa
Giả sử có hai đại lượng biến thiên x
và y trong đó x nhận giá trị thuộc tập
số D.
KN: SGK
Trang 2
Từ ví dụ 2 hãy chỉ ra các giá trị của hàm số trên tại x = 2001 ; 2004 ; 1999.
Hoạt động 3: Cách cho hàm số bằng biểu đồ
Từ ví dụ 2( SGK) hãy chỉ ra các giá trị của mỗi hàm số trên tại các giá trị x
D
Hoạt động 4 : Hàm số cho bằng công thức
HĐ của GV HĐ của HS Nội dung
- Hãy kể tên các hàm số đã
học ở bậc THCS.
- Các bi
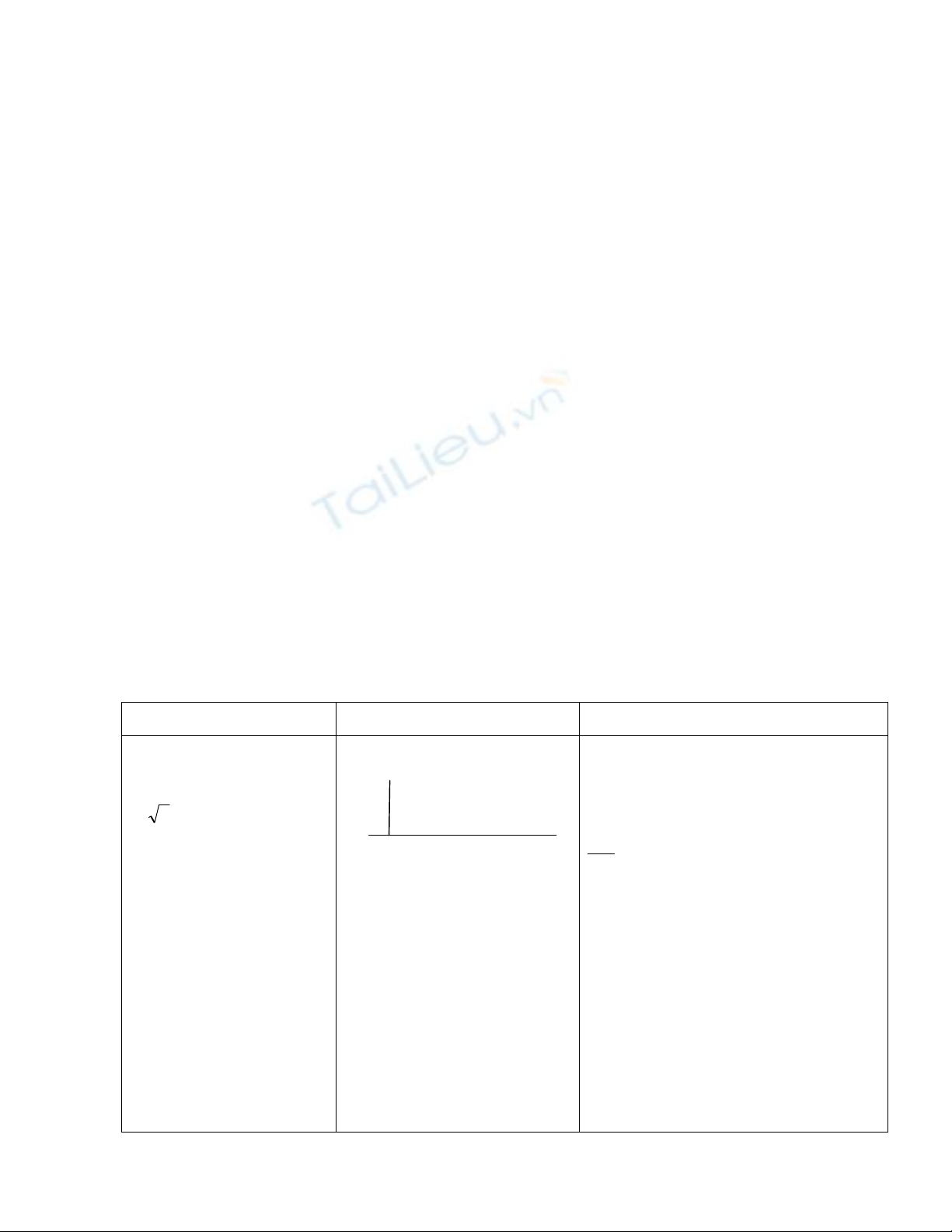
ểu thức y = ax + b,
y =
x
a, y = ax2 có phải là
hàm số không ?
Điều kiện đề nó có nghĩa.
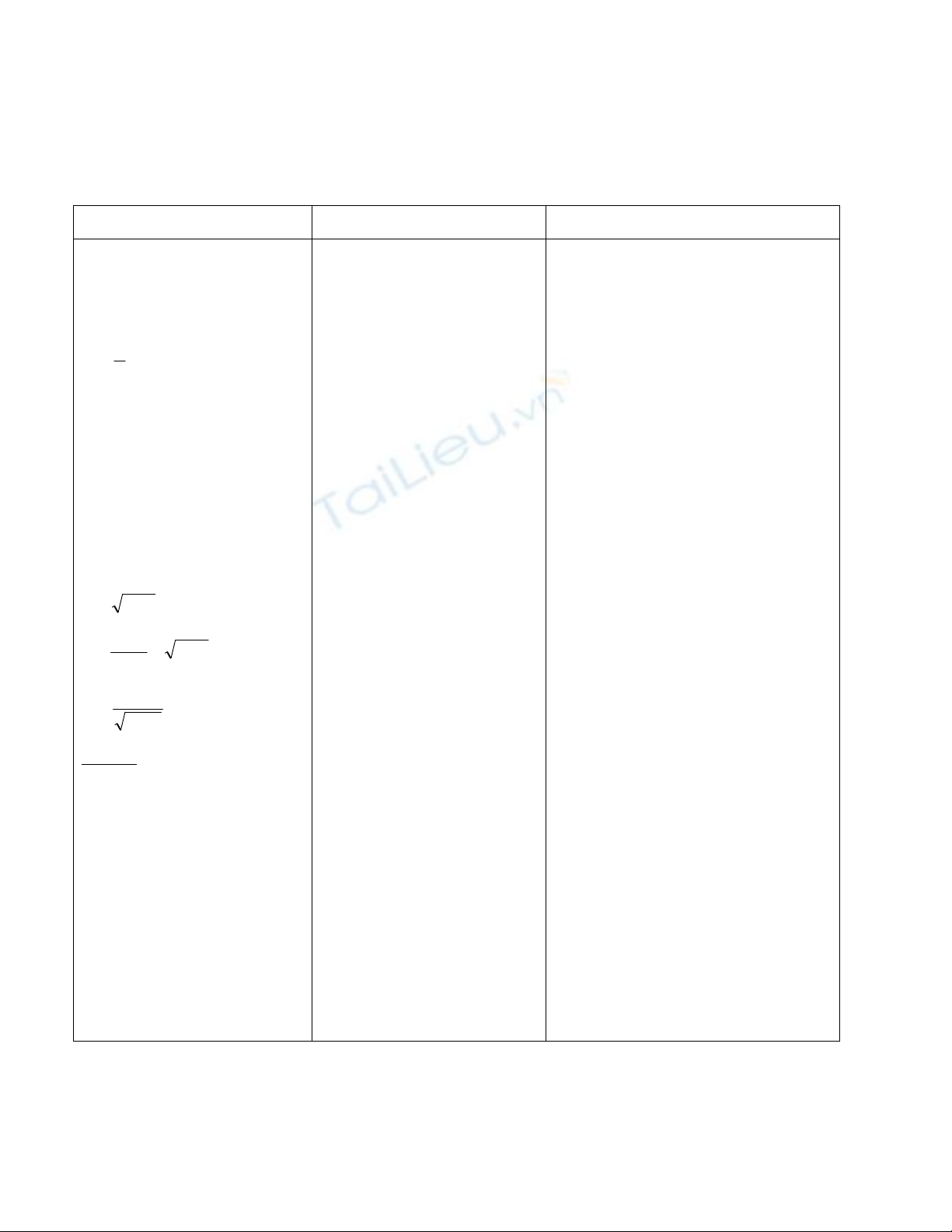
Vd: Tìm tập xác định của
các hàm số:
1 xy
1
2
1
x
x
y
x
y
2
2
Chú ý Với hàm số có thể
được xác định bởi hai, ba, …
công thức. Chẳng hạn cho
hàm số:
0
012
2xkhix
xkhix
y
Hãy tính giá trị của hàm số
này tại x = -2 và x = 5
- Mỗi nhóm cho một ví
dụ về hàm số đã học
ở cấp 2
- Các nhóm trả lời
- Hoàn thiện đưa ra câu
trả lời đúng
- Hình thành kiến thức
- Từng nhóm nhận nhiệm
vụ
Và giải quết vấn đề
- Đưa ra kết quả
- KL
+ Hàm số cho bởi công thức có
dạng: y = f(x)
+ Tập xác định của hàm số y =
f(x) là tập tất cả các số thưcx sao
cho biểu thức f(x) có nghĩa.
Hoạt động 5: Đồ thị của hàm số
Trang 3
Hoạt động 6: Sự biiến thiên của hàm số
HĐ của GV HĐ của HS Nội dung
1. Ôn tập
SGK trang 36
HĐ của GV HĐ của HS Nội dung
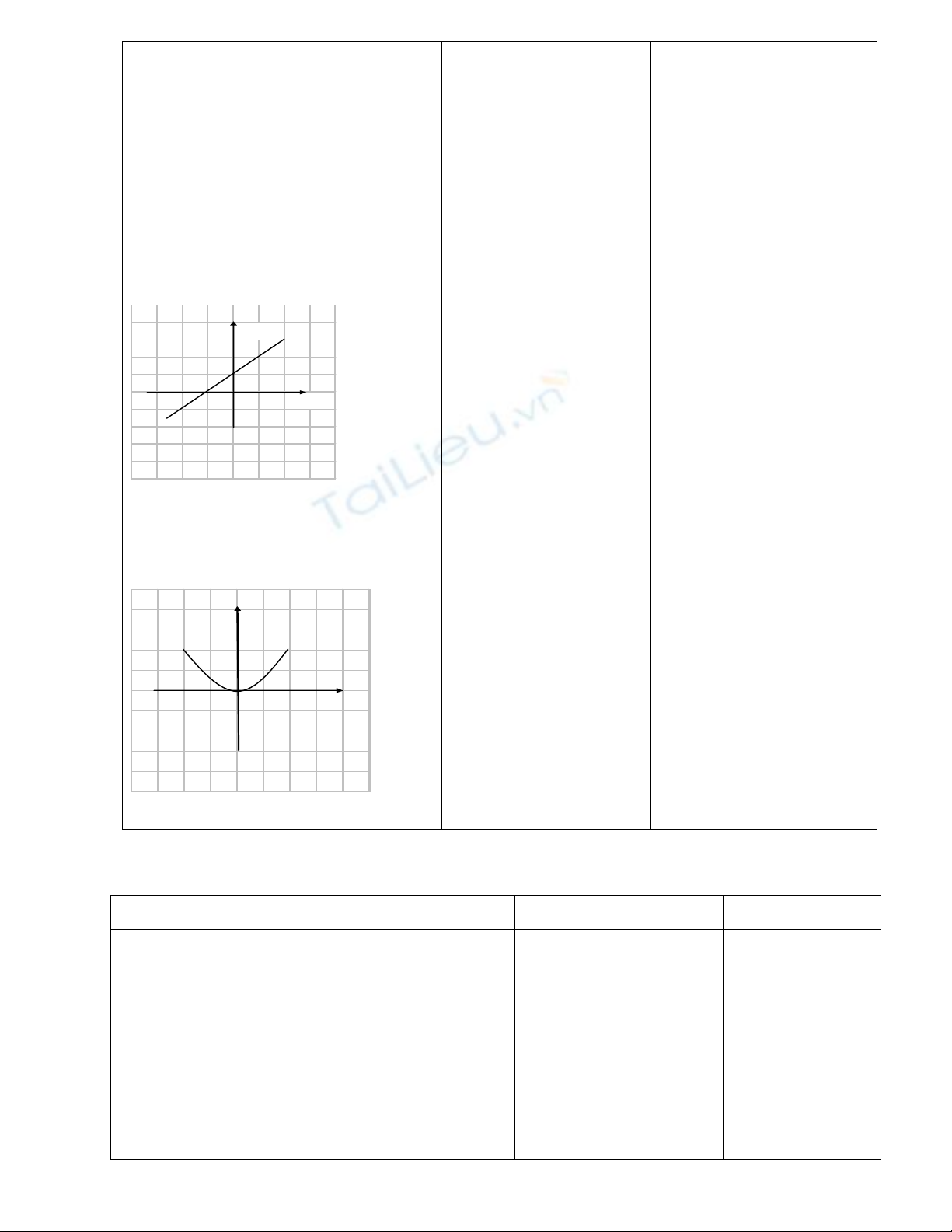
VD1: Dựa vào đồ thị của hai hàm số
sau , hãy tính
a) f(-2), f(-1), f(0), f(2), g(-1), g(-
2), g(0).
b) Tìm x sao cho f(x) = 2
Tìm x sao cho g(x) = 2
y
1
-1
x
VD2: Xét xem trong các đểm A(0 ; 1),
B(1; 0), C(-2 ; -3), D(-3 ; 19), điểm nào
thuộc đồ thị hàm số y = f(x) = 2x2 + 1
y
2
1
-1 0 1 x
- Các nhóm lần lượt đưa
ra kết quả
- Tổng hợp kết quả
- Hình thành kiến thức
- Các nhóm lần lượt
đưa ra kết quả
- Hoàn thiện , đưa ra
kết quả đúng.
Đồ thị của hàm số y = f(x)
xác định trên tập D là tập
hợp tất cả các điểm M(x,
f(x)) trên mặt phẳng tọa độ
với mọi x thuộc D.
Trang 4
y
0 x
y
f(x2)
f(x1)
0 x1 x2 x
y
f(x2)
f(x1)
x1 x2 0
x
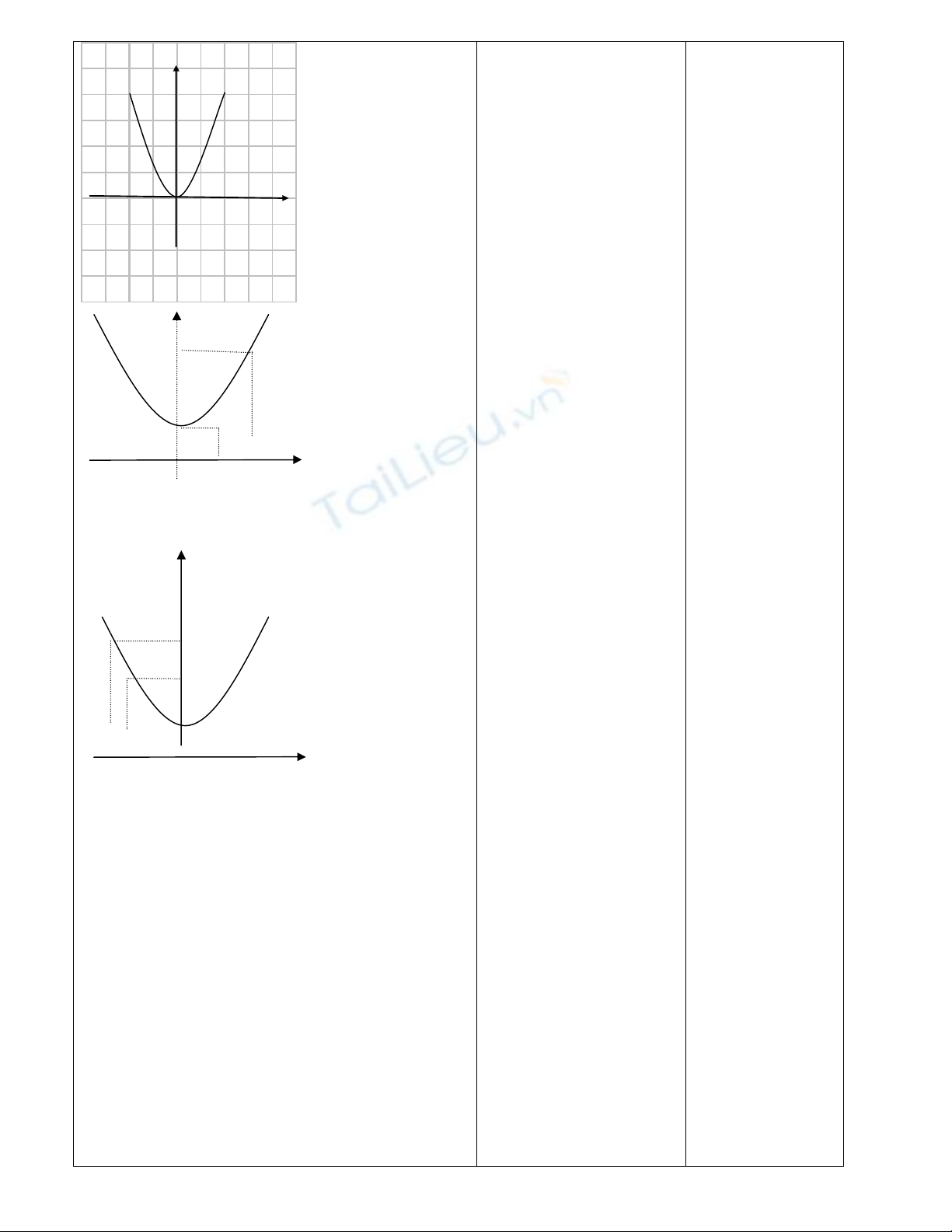
Trên khoảng (0 ; +
) đồ thị đi lên hay xuống từ
trái sang phải
Trên khoảng (-
: 0) đồ thị đi lên hay xuống từ
trái sang phải
2. Bảng biến thiên
+ Dựa vào tính đồng biến nghịch biến của
hàm số lập bảng biến thiên.
+ Lưu ý hàm số đồng biến ta mô tả bằng mũi
tên đi lên, còn hàm số nghịch biến ta mô tả
bằng mũi tên đi xuống.
VD: Vẽ bảng biến thiên của hàm số y = - x2
- Các nhóm trả lời
- Chỉnh sửa (nếu có)
- Hình thành khái niệm.
- Các nhóm cho kết quả
của công việc.
- Hoàn chỉnh kết quả
- Hình thành kiến thức
Trang 5
Hoạt động 7: Củng cố bằng bài tập
Xét tính đồng biến , nghịch biến của các hàm số sau trên khoảng đã chỉ ra:
a) y = -3x + 1 trên R
b) y = 2x2 trên (0 ; +
)
TIẾT 2
Hoạt động 8: Hàm số chẵn, hàm số lẻ và đồ thị của hàm số chẵn lẻ
1) Hàm số chẵn, hàm số lẻ
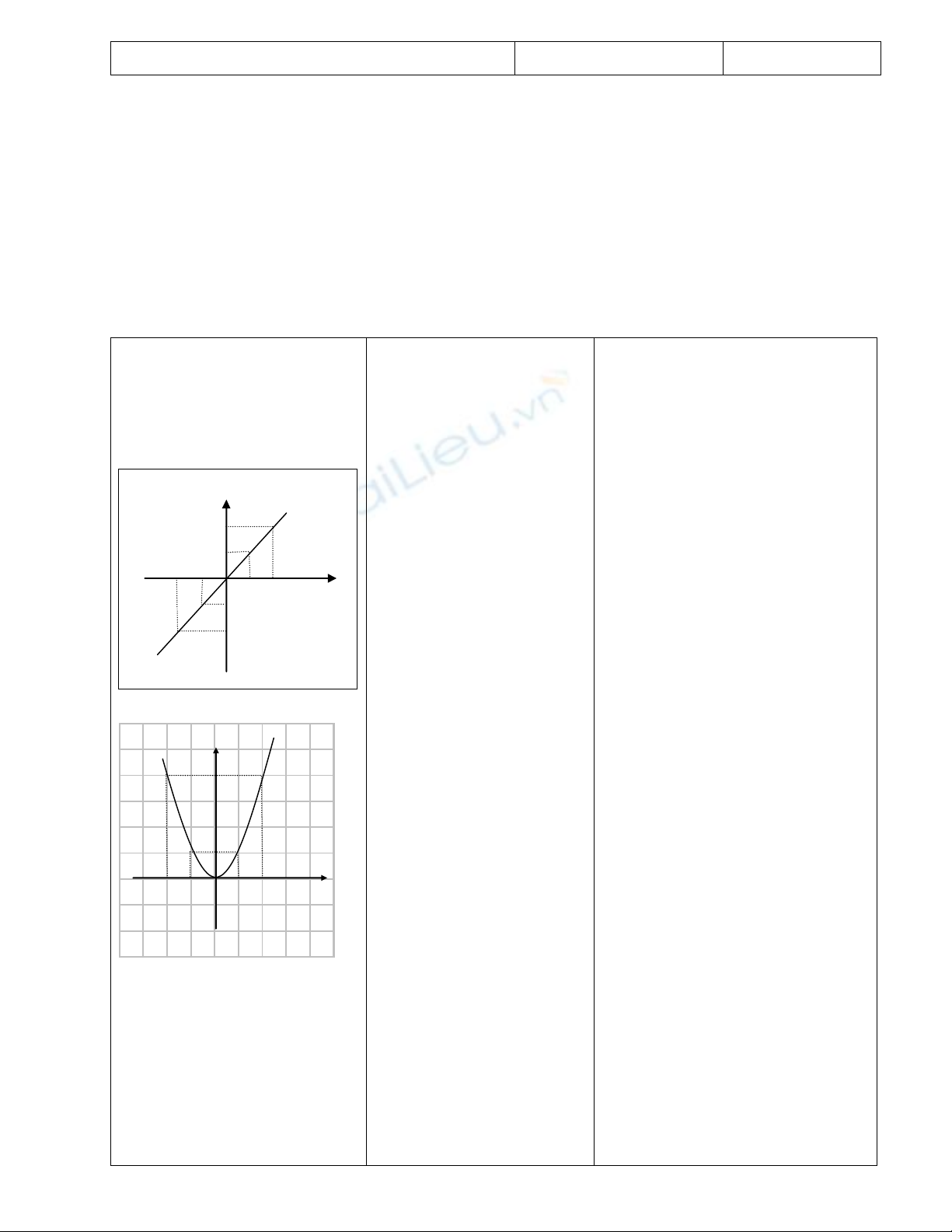
Xét đồ thị của hai hàm số
y = f(x) = x2 và y = g(x) = x
y
-2 -1 0 1 2 x
- TXĐ của hàm số f(x) ?
1 và -1 , 2 và -2 có thuộc
TXĐ không ?
Tính và so sánh f(-1) và f(1)
f(-2) và f(2)
- TXĐ của hàm số g(x) ?
-2
-1