CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025 Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ SÁCH GIÁO KHOA
a) Khái niệm tính đơn điệu của hàm số
Giả sử
K
là một khoảng, một đoạn hoặc một nửa khoảng và
( )y f x
là hàm số xác định trên
K
.
- Hàm số
( )y f x
được gọi là đồng biến trên
K
nếu
1 2 1 2 1 2
, ,x x K x x f x f x
.
- Hàm số
( )y f x
được gọi là nghịch biến trên
K
nếu
1 2 1 2 1 2
, ,x x K x x f x f x
.
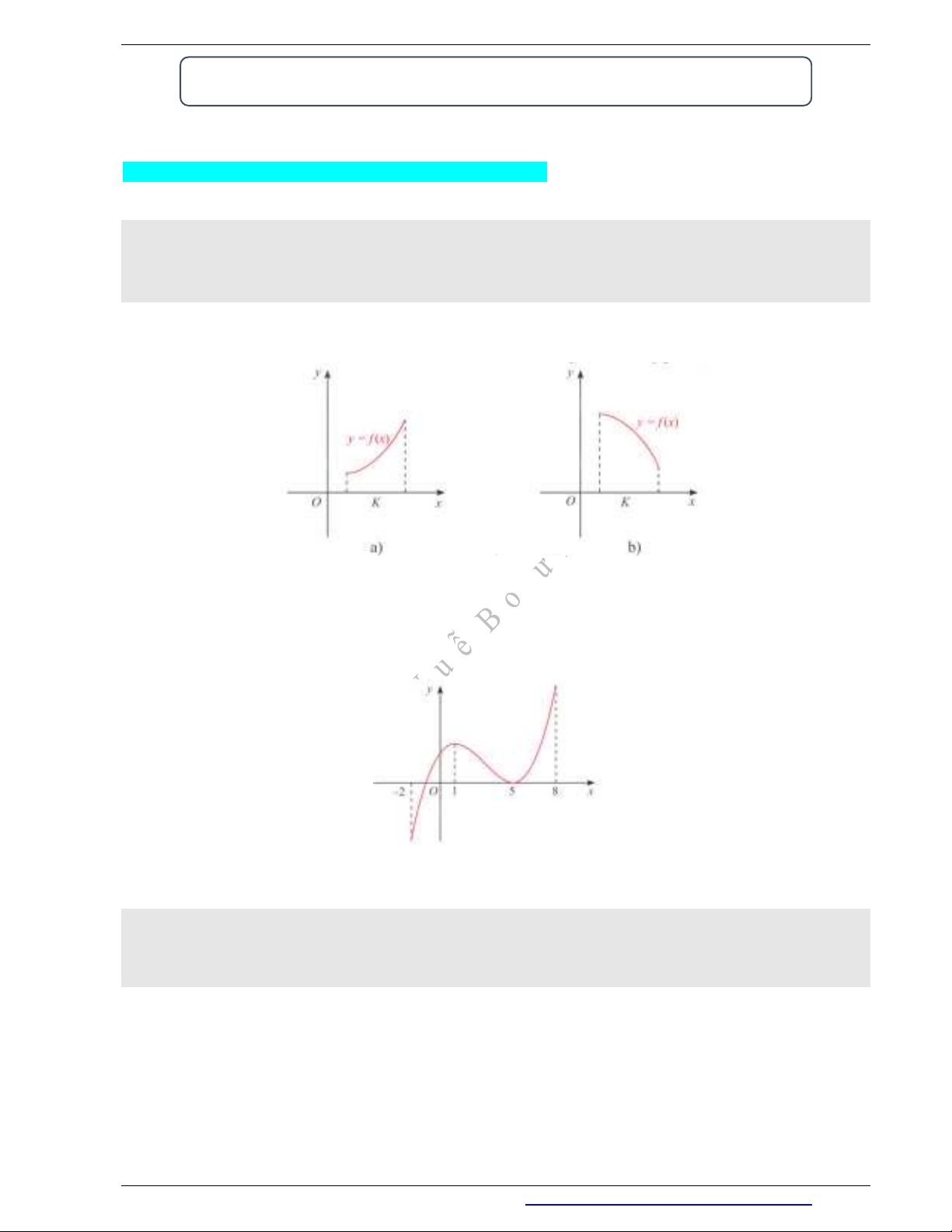
Chú ý
- Nếu hàm số đồng biến trên
K
thì đồ thị của hàm số đị lên từ trái sang phải (H.a).
- Nếu hàm số nghịch biến trên
K
thì đồ thị của hàm số đi xuống từ trái sang phải (H.b).
- Hàm số đồng biến hay nghịch biến trên
K
còn được gọi chung là đơn điệu trên
K
. Việc tìm các khoảng
đồng biến, nghịch biến của hàm số còn được gọi là tìm các khoảng đơn điệu (hay xét tính đơn điệu) của
hàm số.
- Khi xét tính đơn điệu của hàm số mà không chỉ rõ tập
K
thì ta hiểu là xét trên tập xác định của hàm số
đó.
Ví dụ 1. Tìm các khoảng đơn điệu của hàm số
( )y f x
có đồ thị cho ở Hình.
Giải
Hàm số đồng biến trên các khoảng
( 2;1)
và
(5;8)
, nghịch biến trên khoảng
(1;5)
.
ĐỊNH LÍ
Cho hàm số
( )y f x
có đạo hàm trên khoảng
K
.
a) Nếu
( ) 0f x
với mọi
x K
thì hàm số
( )f x
đồng biến trên khoảng
K
.
b) Nếu
( ) 0
f x
với mọi
x K
thì hàm số
( )f x
nghịch biến trên khoảng
K
.
Chú ý
- Định lí trên vẫn đúng trong trường hợp
( )f x
bằng 0 tại một số hữu hạn điểm trong khoảng
K
.
- Người ta chứng minh được rằng, nếu
( ) 0
f x
với mọi
x K
thì hàm số
( )f x
không đổi trên khoảng
K
.
Ví dụ 2. Tìm các khoảng đồng biến, khoảng nghịch biến của hàm số
2
4 2y x x
.
Giải
Tập xác định của hàm số là
.
Ta có:
2 4; 0y x y
với
(2; ); 0x y
với
( ;2)x 
.
CHUYÊN ĐỀ 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
• Fanpage: Nguyễn Bảo Vương - https://www.nbv.edu.vn/
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Do đó, hàm số đồng biến trên khoảng
(2; )
, nghịch biến trên khoảng
( ;2)
.
b) Sử dụng bảng biến thiên xét tính đơn đlệu của hàm số
Các bước để xét tính đơn điệu của hàm số
( )y f x
:
1. Tìm tập xác định của hàm số.
2. Tính đạo hàm
( )f x
. Tìm các điểm
( 1,2, )
i
x i
mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
3. Sắp xếp các điểm
i
x
theo thứ tự tăng dần và lập bảng biến thiên của hàm số.
4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số.
Ví dụ 3. Tìm các khoảng đơn điệu của hàm số
2
2 5
1
x x
yx
.
Giải
Tập xác định của hàm số là
\{1}
.
Ta có:
22
2 2
(2 2)( 1) 2 5 2 3; 0 1
( 1) ( 1)
x x x x x x
y y x
x x
hoặc
3x
.
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có:
Hàm số đồng biến trên các khoảng
( ; 1)
và
(3; )
.
Hàm số nghịch biến trên các khoảng
( 1;1)
và
(1;3)
.
Ví dụ 4. Xét chiều biến thiên của hàm số
2
1
x
y
x
.
Giải
Tập xác định của hàm số là
\{ 1}
.
Ta có:
2 2
( 1) ( 2) 3 0
( 1) ( 1)
x x
yx x
, với mọi
1x
.
Lập bảng biến thiên của hàm số:
Từ bảng biến thiên, ta có: Hàm số đồng biến trên các khoảng
( ; 1)
và
( 1; ) 
.
Ví dụ 5. Tìm các khoảng đơn điệu của hàm số
3 2
15
3
y x x x
.
Giải
- Hàm số đã cho có tập xác định là
.
- Ta có:
2 2
2 1 ( 1)
y x x x
;
0, và 0 1.
y x y x
Bảng biến thiên của hàm số như sau:
Vậy hàm số nghịch biến trên
.
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
PHẦN B. BÀI TẬP TỰ LUẬN
Dạng 1. Xét tính đơn điệu của hàm số cho trước
Từ kết quả trên, để xét tính đơn điệu của hàm số
( )y f x
, ta thực hiện các bước sau:
Bước 1. Tìm tập xác định
D
của hàm số.
Bước 2. Tính đạo hàm
( )f x
của hàm số. Tìm các điểm
1 2
; ; ;
n
x x x
thuộc
D
mà tại đó đạo
hàm
( )f x
bằng 0 hoặc không tồn tại.
Bước 3. Sắp xếp các điểm
1 2
; ; ;
n
x x x
theo thứ tự tăng dần, xét dấu
( )f x
và lập bảng biến
thiên.
Bước 4. Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
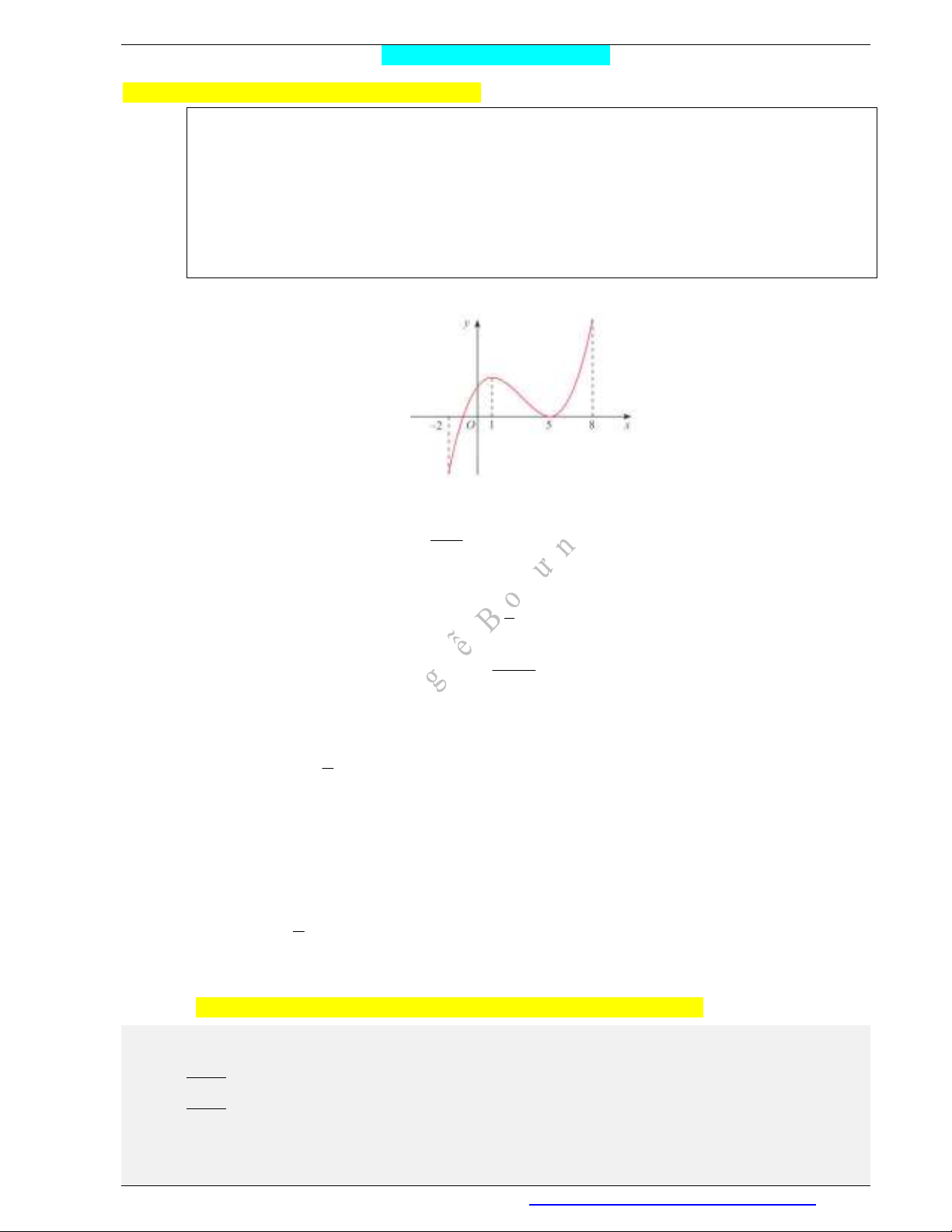
Câu 1. Tìm các khoảng đơn điệu của hàm số
( )y f x
có đồ thị cho ở Hình.
Câu 2. Xét dấu
y
rồi tìm khoảng đồng biến, nghịch biến của hàm số
2
2 4 3 y x x
Câu 3. Chứng minh rằng hàm số
( ) 1
x
g x x
nghịch biến trên khoảng
(1; )
.
Câu 4. Tìm các khoảng đơn điệu của hàm số
3 2
3 9 1. y x x x
Câu 5. Tìm các khoảng đơn điệu của hàm số
3 2
15
3
y x x x
.
Câu 6. Tìm các khoảng đơn điệu của hàm số
2
4
x
yx
.
Câu 7. Xác định các khoảng đồng biến, nghịch biến và lập bảng biến thiên của hàm số:
a)
3 2
( ) 3 1y f x x x
;
b)
1
( )y f x x x
.
Câu 8. Lập bảng biến thiên và xác định các khoảng đơn điệu của hàm số:
3 2
( ) 2 6 6 9y f x x x x
Câu 9. Xét tính đơn điệu của các hàm số sau:
a)
3 2
( ) 3f x x x
b)
1
( )g x x x
c)
3
( )h x x
.
Dạng 2. Tìm m để hàm số đơn điệu trên các khoảng xác định của nó
Xét hàm số bậc ba
3 2
( ) .y f x ax bx cx d
– Đáp ánước 1. Tập xác định:
.D
– Đáp ánước 2. Tính đạo hàm
2
( ) 3 2 .y f x ax bx c
+ Để
( )f x
đồng biến trên
( )
2
( )
3 0
( ) 0, ?
4 12 0
f x
f x
a a
y f x x m
b ac
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
+ Đề
( )f x
nghịch biến trên
( )
2
( )
3 0
( ) 0, ?
4 12 0
f x
f x
a a
y f x x m
b ac
Lưu ý: Dấu của tam thức bậc hai
2
( ) .f x ax bx c
Để
( ) 0,
a
f x x
0
( ) 0,
0
a
f x x
Xét hàm số nhất biến
( )
ax b
y f x
cx d
– Đáp ánước 1. Tập xác định:
\
d
D
c
– Đáp ánước 2. Tính đạo hàm
2
. .
( )
( )
a d b c
y f x
cx d
+ Để
( )f x
đồng biến trên
( ) 0, . . 0 ?D y f x x D a d b c m
+ Để
( )f x
nghịch biến trên
( ) 0, . . 0 ?D y f x x D a d b c m
Lưu ý: Đối với hàm phân thức thì không có dấu
" "
xảy ra tại vị trí
.y
Câu 10. (Đề Tham Khảo Lần 2 2020) Có bao nhiêu giá trị nguyên của tham số
m
sao cho hàm số
3 2
1
( ) 4 3
3
f x x mx x
đồng biến trên
.
Câu 11. (Mã 123 - 2017) Cho hàm số
3 2
4 9 5
y x mx m x , với m là tham số. Hỏi có bao
nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng
 
;
Câu 12. Tìm giá trị của
m
để hàm số
3 2
1– 2 3 – 5
3
y x mx m x m
đồng biến trên
Câu 13. (Đề Tham Khảo - 2017) Hỏi có bao nhiêu số nguyên
m
để hàm số
2 3 2
1 1 4y m x m x x
nghịch biến trên khoảng
;

.
Câu 14. Hỏi có tất cả bao nhiêu giá trị nguyên của tham số
m
để hàm số hàm số
2 3 2
1
2 3 2
3
y m m x mx x
đồng biến trên khoảng
;

?
Câu 15. (Mã 105 - 2017) Cho hàm số
2 3mx m
y
x m
với
m
là tham số. Gọi
S
là tập hợp tất cả các
giá trị nguyên của
m
để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của
S
.
Câu 16. (THPT Hà Huy Tập - 2018) Tìm tất cả giá trị thực của tham số
m
để hàm số
2
1
x m
y
x
nghịch
biến trên các khoảng mà nó xác định?
Dạng 3. Tìm m để hàm số nhất biến đơn điệu trên khoảng cho trước
Câu 17. (Đề Tham Khảo Lần 1 2020) Cho hàm số
4
mx
f x
x m
(
m
là tham số thực). Có bao nhiêu
giá trị nguyên của
m
để hàm số đã cho đồng biến trên khoảng
0;
?
Điện thoại: 0946798489 CHUYÊN ĐỀ ÔN THI TỐT NGHIỆP 2025
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 18. (Mã 103-2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
1
3
x
y
x m
nghịch biến
trên khoảng
6;

?
Câu 19. (Mã 102 - 2018) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
6
5
x
y
x m
nghịch
biến trên khoảng
10;

?
Câu 20. (Sở Hà Tĩnh - 2020) Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
9
4
mx
y
x m
nghịch
biến trên khoảng
0;4
?
Dạng 4. Tìm m để hàm số bậc 3 đơn điệu trên khoảng cho trước
Câu 21. (Mã 101 – 2020 -Lần 2) Tìm tập hợp tất cả các giá trị thực của tham số
m
để hàm số
3 2
3 4
y x x m x
đồng biến trên khoảng
2;

Câu 22. (Mã 102 – 2020 – Lần 2) Tìm tập hợp tất cả các giá trị của tham số
m
để hàm số
3 2
3 5
y x x m x
đồng biến trên khoảng
2;
Câu 23. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
32
( ) 7 14 2
3
mx
y f x mx x m
giảm trên nửa khoảng
[1; )
?
Câu 24. Tìm tất cả các giá thực của tham số
m
sao cho hàm số
3 2
2 3 6
y x x mx m
nghịch biến
trên khoảng
1;1
.
Câu 25. (THPT Chuyên Hạ Long - 2018) Gọi
S
là tập hợp các giá trị nguyên dương của
m
để hàm
số
3 2
3 2 1 12 5 2
y x m x m x
đồng biến trên khoảng
2;
. Tìm số phần tử của
S
Dạng 5. Tìm m để hàm số (lượng giác, chứa căn, chứa dấu giá trị tuyệt đối…) đơn điệu
trên khoảng cho trước
Câu 26. (Đề Minh Họa 2017) Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số
tan 2
tan
x
y
x m
đồng biến trên khoảng
0; .
4
Câu 27. (Đề Tham Khảo 2018) Có bao nhiêu giá trị nguyên âm của tham số
m
để hàm số
3
5
1
5
y x mx
x
đồng biến trên khoảng
0;
Câu 28. (THPT Bạch Đằng Quảng Ninh 2019) Gọi
S
là tập hợp tất cả các giá trị của tham số
m
để
hàm số
2 5 3 2 2
1 1
10 20
5 3
f x m x mx x m m x
đồng biến trên
. Tính tổng giá trị của tất cả các
phần tử thuộc
S
Câu 29. (THPT Lê Quý Đôn Đà Nẵng 2019) Tìm tập hợp các giá trị thực của tham số m để hàm số
1
2
m
y x
x
đồng biến trên mỗi khoảng xác định của nó?
Câu 30. (THPT Minh Khai Hà Tĩnh 2019) Tìm tất cả các giá trị thực của tham số để hàm số
cos 3
cos
x
y
x m
nghịch biến trên khoảng
;
2