CHUYÊN ĐỀ VD-VDC TOÁN 12 Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
Dạng 1. Thể tích, diện tích… khối trụ
Câu 1. Một hộp đựng phấn hình hộp chữ nhật có chiều dài
30cm
, chiều rộng
5cm
và chiều cao
6cm
.
Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là một một khối trụ có
chiều cao
6h cm
và bán kính đáy
1
2
r cm
. Hỏi có thể xếp được tối đa bao nhiêu viên phấn?
A.
150
viên. B.
153
viên. C.
151
viên. D.
154
viên.
Câu 2. Cho hình trụ có hai đường tròn đáy là
O
và
O
. Gọi
A
trên đường tròn
O
và
B
trên đường
tròn
O
sao cho
4AB a
. Biết khoảng cách từ đường thẳng
AB
đến trục của hình trụ bằng
a
và
2OO a
. Tính diện tích xung quanh của hình trụ đã cho.
A.
2
42 a
. B.
2
8a
. C.
2
16 a
. D.
2
8a
.
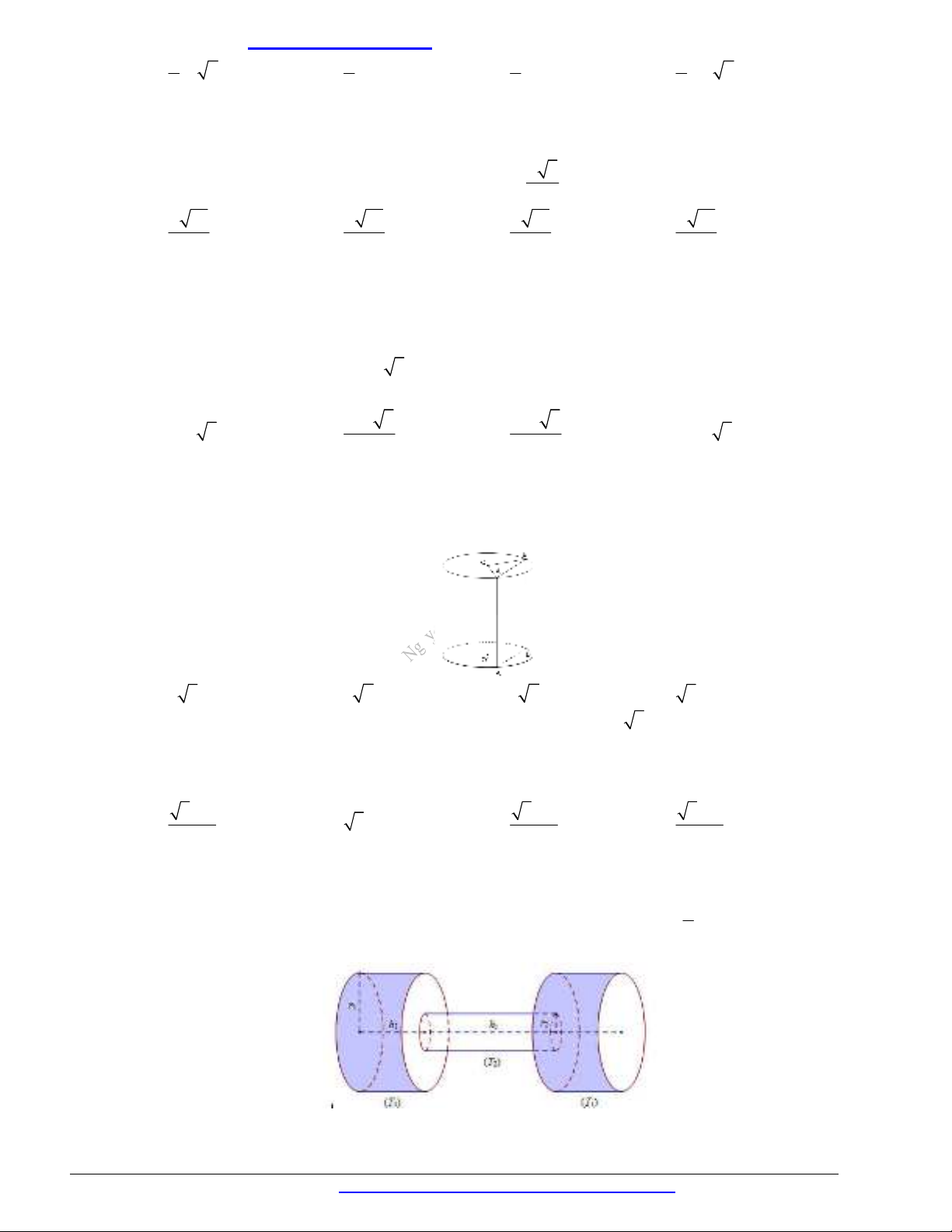
Câu 3. Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao
1,5mh
gồm:
- Phần dưới có dạng hình trụ bán kính đáy
1mR
và có chiều cao bằng
1
3h
;
- Phần trên có dạng hình nón bán kính đáy bằng
R
đã bị cắt bỏ bớt một phần hình nón có bán
kính đáy bằng
1
2R
ở phía trên (người ta thường gọi hình đó là hình nón cụt);
- Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng
1
4R
(tham khảo hình vẽ bên dưới).
Thể tích của khối bê tông (làm tròn đến chữ số thập phân thứ ba) bằng
A.
3
2,815m. B.
3
2,814m. C.
3
3,403m. D.
3
3,109m.
Câu 4. Người ta thiết kế một thùng chứa hình trụ (như hình vẽ) có thể tích
V
nhất định. Biết rằng giá của
vật liệu làm mặt đáy và nắp của thùng bằng nhau và đắt gấp ba lần so với giá vật liệu để làm mặt
xung quanh của thùng (chi phí cho mỗi đơn vị diện tích). Gọi chiều cao của thùng là
h
và bán
kính đáy là
.r
Tính tỉ số
h
r
sao cho chi phí vật liệu sản xuất thùng là nhỏ nhất?
Chuyên đề 20. KHỐI TRỤ
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
A.
2.
h
r
B.
2.
h
r
C.
6.
h
r
D.
3 2.
h
r
Câu 5. Cho hình trụ có hai đáy là hai hình tròn
O
và
,O
thiết diện qua trục của hình trụ là hình
vuông. Gọi
,A B
là hai điểm lần lượt nằm trên hai đường tròn
O
và
.O
Biết
2AB a
và
khoẳng cách giữa hai đường thẳng
AB
và
OO
bằng
3.
2
a
Bán kính đáy bằng
A.
14 .
3
a
B.
14 .
2
a
C.
14 .
4
a
D.
14 .
9
a
Câu 6. Cho hình trụ có chiều cao bằng
8a
. Biết hai điểm
,A C
lần lượt nằm trên hai đáy thỏa
10AC a
,
khoảng cách giữa
AC
và trục của hình trụ bằng
4a
. Thể tích của khối trụ đã cho là
A.
3
128
a
. B.
3
320
a
. C.
3
80
a
. D.
3
200
a
.
Câu 7. Cho hình trụ có
,O O
là tâm hai đáy. Xét hình chữ nhật
ABCD
có
,A B
cùng thuộc
O
và
,C D
cùng thuộc
O
sao cho 3AB a,
2BC a
đồng thời
ABCD
tạo với mặt phẳng đáy hình
trụ góc
60
. Thể tích khối trụ bằng
A.
3
3a
. B.
3
3
9
a
. C.
3
3
3
a
. D.
3
2 3a
.
Câu 8. Một hình trụ có diện tích xung quanh là
4
, thiết diện qua trục là một hình vuông. Một mặt
phẳng
song song với trục, cắt hình trụ theo thiết diện
ABB A
, biết một cạnh của thiết diện là
một dây của đường tròn đáy của hình trụ và căng một cung
0
120
. Diện tích của thiết diện
ABB A
bằng
A. 2 3 . B.
2 2
. C.
3 2
. D. 3 .
Câu 9. Cho hình trụ có hai đáy là hình tròn tâm
O
và
O
, chiều cao 3h a. Mặt phẳng đi qua tâm
O
và tạo với
OO
một góc
30
, cắt hai đường tròn tâm
O
và
O
tại bốn điểm là bốn đỉnh của một
hình thang có đáy lớn gấp đôi đáy nhỏ và diện tích bằng
2
3a
. Thể tích của khối trụ được giới hạn
bởi hình trụ đã cho bằng
A.
3
3
3
a
. B.
3
3a. C.
3
3
12
a
. D.
3
3
4
a
.
Câu 10. Một chiếc tạ tay có hình dạng gồm 3 khối trụ, trong đó hai khối trụ ở hai đầu bằng nhau và khối
trụ làm tay cầm ở giữa. Gọi khối trụ làm đầu tạ là
1
T
và khối trụ làm tay cầm là
2
T
lần lượt có
bán kính và chiều cao tương ứng là
1
r,
1
h,
2
r,
2
h thỏa mãn
1 2
4r r,
1 2
1
2
h h
(tham khảo hình
vẽ).
Biết rằng thể tích của khối trụ tay cầm
2
T
bằng 30
3
cm
và chiếc tạ làm bằng inox có khối
lượng riêng là
3
7,7 /D g cm. Khối lượng của chiếc tạ tay bằng
Điện thoại: 0946798489 CHUYÊN ĐỀ VD-VDC TOÁN 12
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
A.
3,927
kg
. B.
2,927
kg
. C.
3,279
kg
. D.
2,279
kg
.
Câu 11. Cho hình trụ có hai đáy là hai hình tròn
và
,O
bán kính đáy
5.
r
Biết
AB
là một dây
cung của đường tròn
sao cho tam giác
O AB
là tam giác đều và mặt phẳng
O AB
tạo với
mặt phẳng chứa hình tròn
một góc
0
60 .
Thể tích của khối trụ đã cho bằng
A.
25 5
. B.
75 5
. C.
375 7
7
. D.
125 7
7
.
Câu 12. Cho hình trụ có các đáy là
2
hình tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
a
.
Trên đường tròn đáy tâm
O
lấy điểm
A
, trên đường tròn đáy tâm
O
lấy điểm
B
sao cho
2AB a
. Thể tích khối tứ diện
OO AB
theo
a
là
A.
3
3
4
a
V
. B.
3
3
8
a
V
. C.
3
3
6
a
V
. D.
3
3
12
a
V
.
Câu 13. Một khối gỗ có hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy
nào đó ta lấy hai điểm A,B sao cho cung
AB
có số đo
0
120 .
Người ta cắt khúc gỗ bởi một mặt
phẳng đi qua A, B và tâm của hình trụ (tâm của hình trụ là trung điểm của đoạn nối tâm hai đáy)
để được thiết diện như hình vẽ. Biết diện tích
S
của thiết diện thu được có dạng
3S a b
.
Tính
P a b
.
A.
30
P
. B.
45
P
. C.
60
P
. D.
50
P
.
Câu 14. Cho hình trụ
( )T
có chiều cao bẳng
2a
, hai đường tròn đáy của (T) có tâm lần lượt là
1
,O O
, bán
kính bằng
a
. Trên đường tròn đáy tâm
O
lấy điểm
A
, trên đường tròn đáy tâm
1
O
lấy điểm
B
sao
cho
7AB a
. Thể tích khối tứ diện
1
OO AB
bằng:
A.
3
3
6a
. B.
3
3
3a
. C.
3
3
12 a
. D.
3
3
4a
.
Câu 15. Cho hình trụ tròn xoay có hai đáy là hai hình tròn
; 7
O
và
'; 7
O
. Biết rằng tồn tại dây cung
AB
của đường tròn sao cho tam giác
'O AB
là tam giác đều và mặt phẳng
'
O AB
hợp với mặt đáy
của hình trụ một góc bằng
0
60
. Thể tích khối trụ đã cho
là
A.
3 7
. B.
21
. C.
7
. D.
7
.
Câu 16. Người ta cần đổ một ống cống thoát nước hình trụ với chiều cao
2m
, độ dày thành ống là
10cm
.
Đường kính ống là
50cm
. Tính lượng bê tông cần dùng để làm ra ống thoát nước đó?
A.
3
0,045 m
. B.
3
0,12 m
. C.
3
0,08 m
. D.
3
0,5 m
.
Câu 17. Một người thợ có một khối đá hình trụ. Kẻ hai đường kính
,MN PQ
của hai đáy sao cho
.MN PQ
Người thợ đó cắt khối đá theo các mặt cắt đi qua 3 trong 4 điểm
, , ,M N P Q
để thu
được khối đá có hình tứ diện
MNPQ
. Biết rằng
6dm
MN
và thể tích khối tứ diện
MNPQ
bằng
3
36dm
. Tìm thể tích của lượng đá bị cắt bỏ (làm tròn kết quả đến 1 chữ số thập phân).
A.
3
133,6dm
. B.
3
143,6dm
. C.
3
123,6dm
. D.
3
113,6dm
.
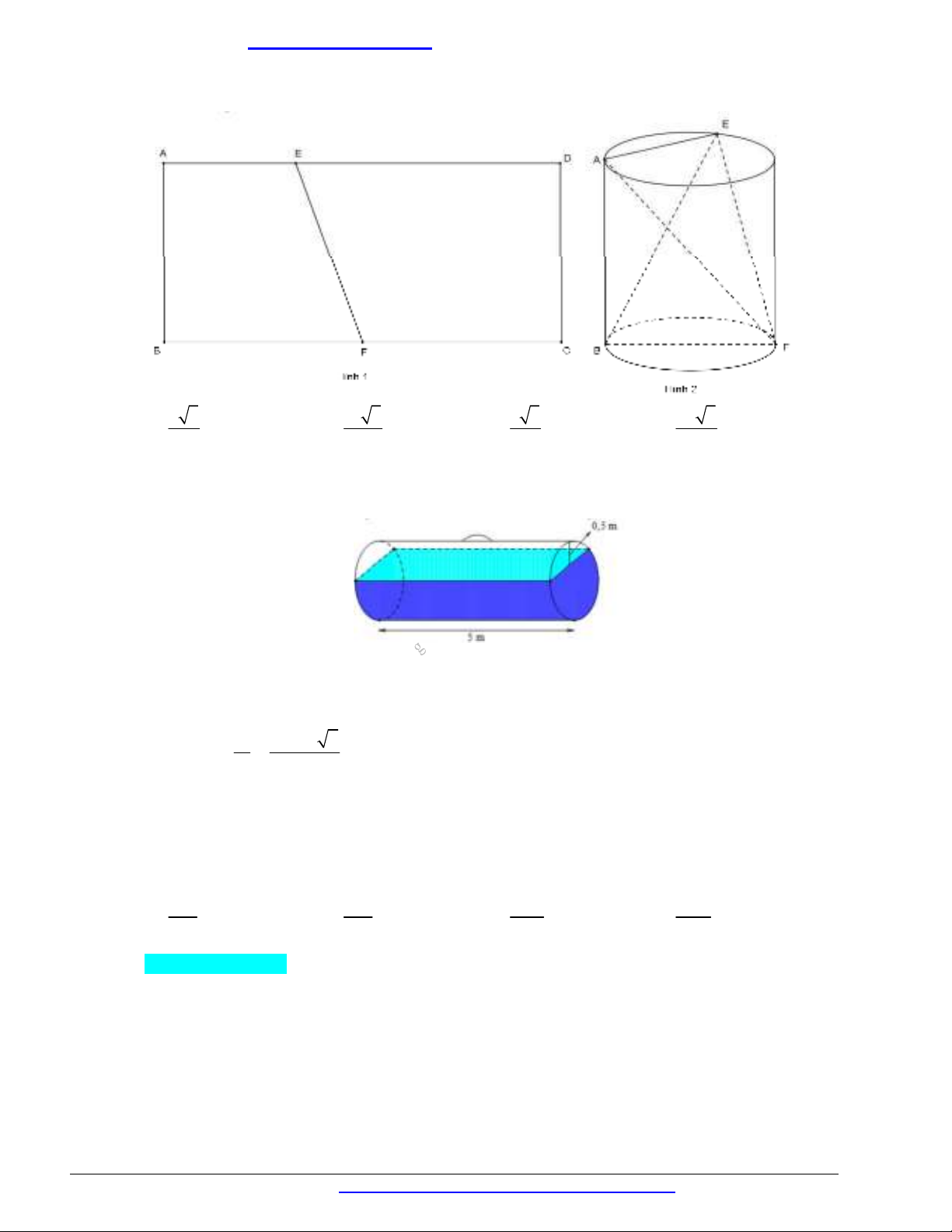
Câu 18. Một miếng tôn mỏng hình chữ nhật
ABCD
với
3dm
AB
và
6dm
AD
. Trên cạnh
AD
lấy
điểm
E
sao cho
2dm
AE
, trên cạnh
BC
lấy điểm
F
là trung điểm
BC
(tham khảo hình
1
).
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Cuộn miếng tôn lại một vòng sao cho cạnh
AB
và
DC
trùng khít nhau. Khi đó miếng tôn tạo
thành mặt xung quanh của một hình trụ (tham khảo hình
2
). Thể tích
V
của tứ diện
ABEF
trong
hình
2
bằng:
A.
3
2
9 3 dm
2
. B.
3
2
81 3 dm
2
. C.
3
2
3 3 dm
2
. D.
3
2
27 3 dm
2
.
Câu 19. Một bồn hình trụ chứa dầu được đặt nằm ngang, có chiều dài
5m
, bán kính đáy
1m
, với nắp bồn
đặt trên mặt nằm ngang của mặt trụ. Người ta rút dầu trong bồn tương ứng với
0,5
m của đường
kính đáy. Tính thể tích gần đúng nhất của khối dầu còn lại trong bồn.
A.
3
11,781m. B.
3
12,637m. C.
3
14,923m. D.
3
8,307m.
Câu 20. Cho trụ có thể tích
V
. Hình lăng trụ đều
.ABC A B C
nội tiếp hình trụ. Mặt phẳng
ABB A
chia
khối trụ làm hai phần có thể tích lần lượt là
1
V và
2
V biết
1 2
V V
.
Khi đó tỉ số
1
12
Va b b
V
với
,a b N
. Tính tổng
T a b
.
A.
16T
. B.
11T
. C.
7T
. D.
14T
.
Câu 21. Có một mảnh bìa hình chữ nhật
ABCD
với
4 , 2 .AB a AD a
Người ta đánh dấu M là trung
điểm của AB, N và P là các điểm thuộc CD sao cho
DN CP a
. Sau đó người ta cuốn mảnh bìa
lại sao cho cạnh
BC
trùng với cạnh
AD
tạo thành một hình trụ. Thể tích của tứ diện
AMNP
với
các đỉnh
, , ,A M N P
nằm trên hình trụ vừa tạo thành bằng
A.
3
2
4
3
a
. B.
3
2
8
3
a
. C.
3
2
16
3
a
. D.
3
2
32
3
a
.
Dạng 2. Min – max
Câu 1. Khi sản xuất vỏ lon sữa bò hình trụ, các nhà thiết kế luôn đặt mục tiêu sao cho chi phí nguyên liệu
làm vỏ lon là ít nhất, tức là diện tích toàn phần của hình trụ là nhỏ nhất. Muốn thể tích khối trụ đó
bằng
2
và diện tích toàn phần hình trụ nhỏ nhất thì bán kính đáy gần số nào nhất?
A.
0,5
. B.
0,6
. C.
0,8
. D.
0,7
.
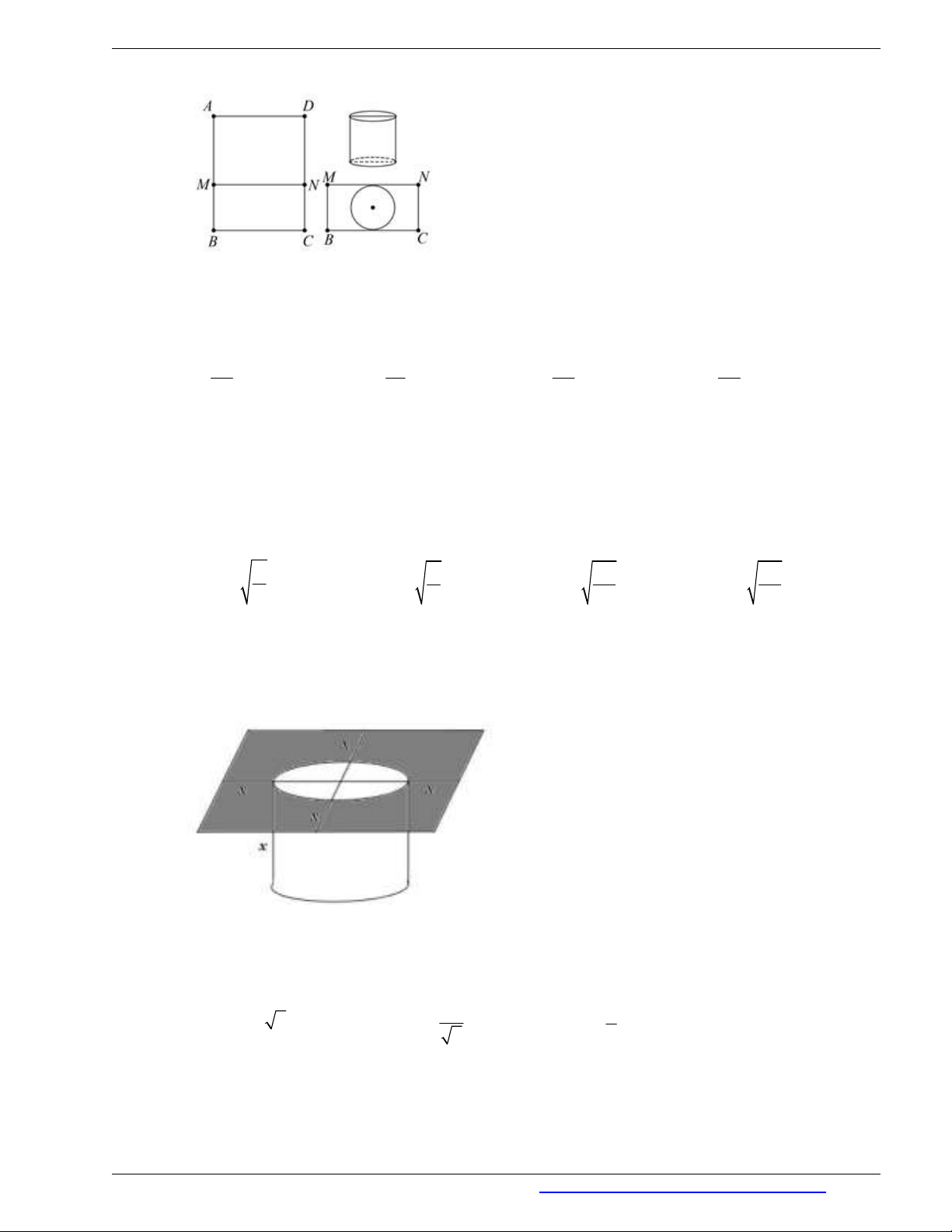
Câu 2. Sử dụng mảnh inox hình chữ nhật
ABCD
có diện tích bằng
2
1m và cạnh
BC x
m
để làm một
thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật
ABCD
thành
hai hình chữ nhật
ADNM
và
BCNM
, trong đó phần hình chữ nhật
ADNM
được gò thành phần
xung quanh hình trụ có chiều cao bằng
AM
; phần hình chữ nhật
BCNM
được cắt ra một hình
Điện thoại: 0946798489 CHUYÊN ĐỀ VD-VDC TOÁN 12
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị
x
để
thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
A.
1,37 m
. B.
1,02 m
. C.
0,97 m
. D.
1m
.
Câu 3. Gia đình An làm bể hình trụ có thể tích
3
150 m
. Đáy bể làm bằng bê tông giá
2
100000 / m
. Phần
thân làm bằng tôn giá
2
90000 / m
, nắp bằng nhôm giá
2
120000m
. Hỏi khi chi phí làm bể đạt mức
thấp nhất thì tỷ số giữa chiều cao bể và bán kính đáy là bao nhiêu?
A.
22
9
. B.
21
32
. C.
31
22
. D.
9
22
.
Câu 4. Anh H dự định làm một cái thùng đựng dầu hình trụ bằng sắt có nắp đậy thể tích
3
12m
. Chi phí
làm mỗi
2
m
đáy là 400 ngàn đồng, mỗi
2
m
nắp là 200 ngàn đồng, mỗi
2
m
mặt xung quanh là 300
ngàn đồng. Để chi phí làm thùng là ít nhất thì anh H cần chọn chiều cao của thùng gần nhất với số
nào sau đây? (Xem độ dày của tấm sắt làm thùng là không đáng kể).
A.
1, 24 m
. B.
1, 25 m
. C.
2,50 m
. D.
2,48m
.
Câu 5. Người ta cần làm một cái bồn chứa dạng hình trụ có thể tích 1000 lít bằng inox để chứa nước, tính
bán kính
R
của hình trụ đó sao cho diện tích toàn phần của bồn chứa có giá trị nhỏ nhất.
A.
3
2
R
. B.
3
1
R
. C.
3
1
2
R
. D.
3
3
2
R
.
Câu 6. Trên một mảnh đất hình vuông có diện tích
2
81m
người ta đào một cái ao nuôi cá hình trụ (như
hình vẽ) sao cho tâm của hình tròn đáy trùng với tâm của mảnh đất. Ở giữa mép ao và mép
mảnh đất người ta để lại một khoảng đất trống để đi lại, biết khoảng cách nhỏ nhất giữa mép ao
và mép mảnh đất là
x m
. Giả sử chiều sâu của ao cũng là
x m
. Tính thể tích lớn nhất V của
ao.
A.
3
13,5
V m
. B.
3
27
V m
. C.
3
36
V m
. D.
3
72
V m
.
Câu 7. Cho hình trụ có đáy là hai đường tròn tâm
O
và
O
, bán kính đáy bằng chiều cao và bằng
2a
.
Trên đường tròn đáy có tâm
O
lấy điểm
A
, trên đường tròn tâm
O
lấy điểm
B
. Đặt
là góc
giữa
AB
và đáy. Tính
tan
khi thể tích khối tứ diện
OO AB
đạt giá trị lớn nhất.
A.
tan 2
B.
1
tan
2
C.
1
tan
2
D.
tan 1
Câu 8. Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi bằng
12
.
Giá trị lớn nhất của thể tích khối trụ là
A.
. B.
32
. C.
8
. D.
64
.
Câu 9. Trong các hình trụ có diện tích toàn phần bằng
2
1000
cm
thì hình trụ có thể tích lớn nhất là bao
nhiêu
3
cm