§¹i häc ®µ n½ng
Tr−êng ®¹i häc B¸ch KHOA
khoa s− ph¹m kü thuËt
-------¶ ·-------
bµi gi¶ng
c¬ häc ®¹i c−¬ng - MÐcanique gÐnÐrale
(C¥ Häc vËt r¾n – dao ®éng vµ sãng c¬)
dïng cho sinh viªn ch−¬ng tr×nh ®µo t¹o kü s− chÊt l−îng cao
(L¦U HµNH NéI Bé)
Biªn so¹n :
L£ CUNG - Khoa s− ph¹m kü thuËt
®µ n¨ng 2006

Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
PHÁÖN I :
CÅ HOÜC VÁÛT RÀÕN
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Chæång än táûp:
MÄÜT SÄÚ KHAÏI NIÃÛM VAÌ ÂËNH LYÏ CÅ BAÍN
CUÍA ÂÄÜNG HOÜC VAÌ ÂÄÜNG LÆÛC HOÜC HÃÛ CHÁÚT
§1. Håüp váûn täúc - Håüp gia täúc :
Xeït hãû quy chiãúu (R2) chuyãøn âäüng tæång âäúi so våïi hãû quy
chiãúu (R1). Goüi vaì
1111
(; , , )
xyz
Oe e e
GGG
2222
(; , , )
xyz
Oe e e
G
GG laì hai hãû
toüa âäü Descartes láön læåüt gàõn liãön våïi (R1) vaì (R2).
ez2
1) Chuyãøn âäüng tæång âäúi cuía hai hãû quy chiãúu :
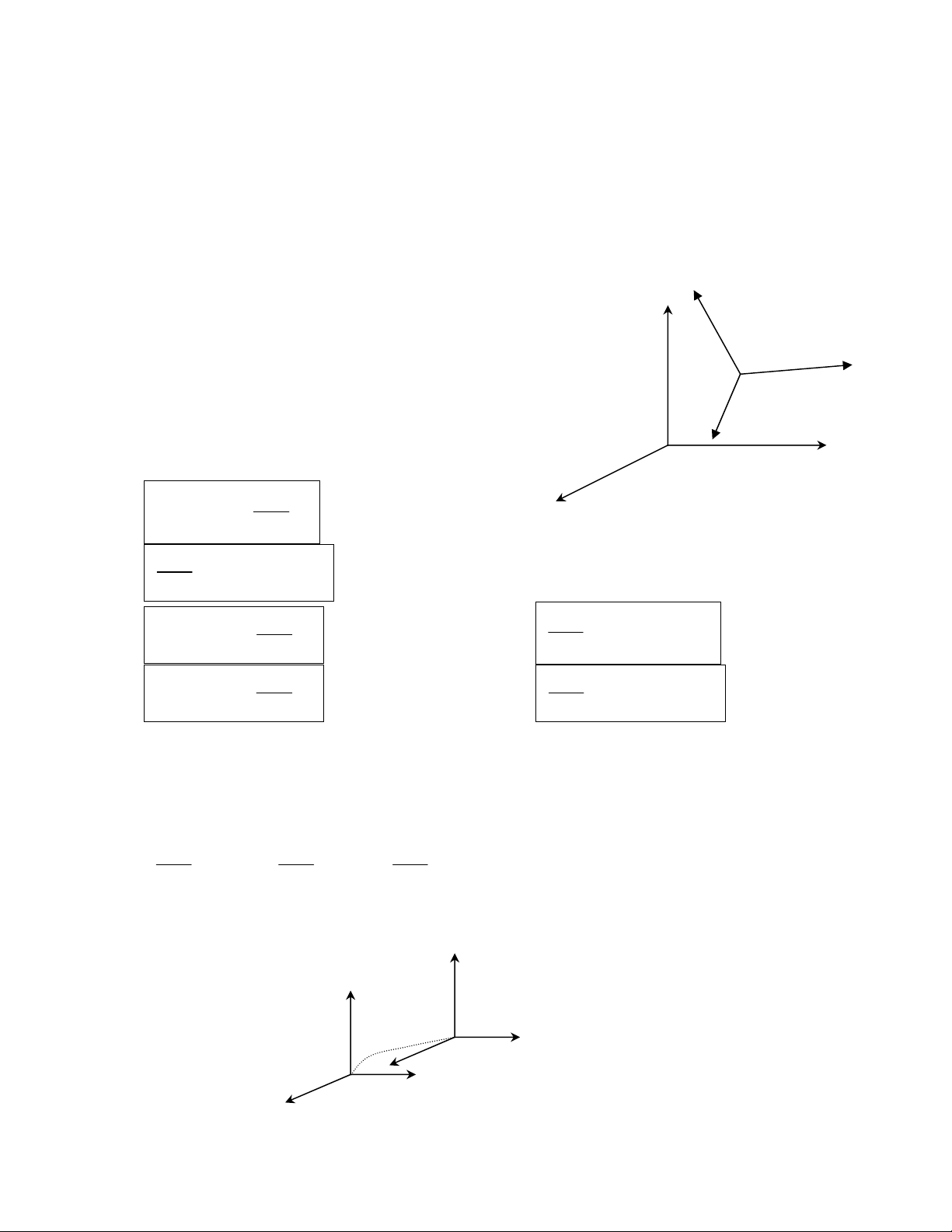
a) Veïctå quay :
Vectå quay 2/ 1
R
R
Ω
G
cuía hãû quy chiãúu (R2) âäúi våïi hãû quy
chiãúu (R1) :
R2/R1 2 2 2 2 2 2
...
x
xyyz
eeΩ=Ω +Ω +Ω
z
e
GGG
Gvåïi :
2
22
/1
() . y
xz
R
de
te dt
⎛⎞
Ω=
⎜⎟
⎝⎠
G
G
Suy ra :
2
2/ 1 2
/1
x
R
Rx
R
de e
dt
⎛⎞
=Ω ×
⎜⎟
⎝⎠
GGG
O2
e
y
2
ex2
e
y
1
ez1
1
()
R
2
()
R
O1
ex1
2
22
/1
() . z
yx
R
de
te dt
⎛⎞
Ω=
⎜⎟
⎝⎠
G
G
2
2/ 1 2
/1
y
R
Ry
R
de e
dt
⎛⎞
=
Ω×
⎜⎟
⎝⎠
G
G
G
2
22
/1
() . x
zy
R
de
te dt
⎛⎞
Ω=
⎜⎟
⎝⎠
G
G
2
2/ 1 2
/1
z
R
Rz
R
de e
dt
⎛⎞
=
Ω×
⎜⎟
⎝⎠
G
G
G
Vectå âàûc træng cho chuyãøn âäüng quay cuía hãû (R2) âäúi våïi hãû (R1) vaì âæåüc goüi laì vectå
quay keïo theo.
2/ 1RR
Ω
G
b) Træåìng håüp (R2) chuyãøn âäüng tënh tiãún tæång âäúi so våïi (R1) :
G
Ta coï : Ω=
2/ 1 0
RR
⇒ 2
/1
0
x
R
de
dt
⎛⎞
=
⎜⎟
⎝⎠
G
; 2
/1
0
y
R
de
dt
⎛⎞
⎜⎟ ;
=
⎝⎠
G
2
/1
0
z
R
de
dt
⎛⎞
=
⎜⎟
⎝⎠
G
O1
z1
y1
1
()
R
z2
x2
O2
2
()
R
x1
y2
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
⇒ Caïc veïctå vaì moüi vectå gàõn liãön våïi hãû quy chiãúu (R2) âãöu laì khäng âäøi trong hãû
quy chiãúu (R1).
22
,,
xyz
eee
GGG
2
Váûn täúc 12
2/1
/1
()
R
R
dOO
vO âàûc træng cho chuyãøn âäüng tënh tiãún cuía hãû (R2) so våïi hãû (R1).
dt
⎛⎞
=⎜⎟
⎝⎠
JJJJJG
G
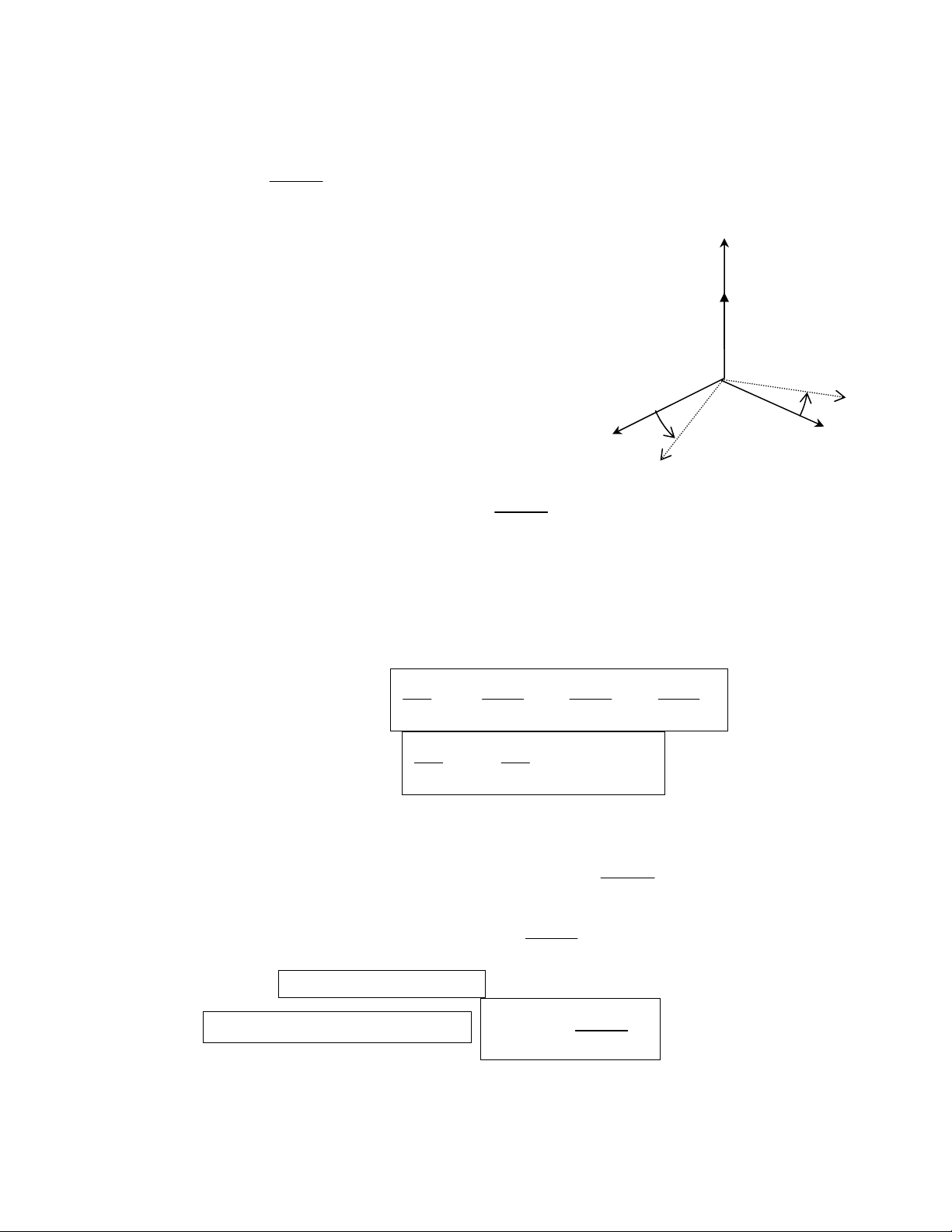
b) Træåìng håüp hãû (R2) quay tæång âäúi xung quanh mäüt truûc cäú âënh cuía hãû (R1):
Giaí sæí hãû quy chiãúu (R2) quay xung quanh truûc cäú âënh (O1z1)
cuía hãû quy chiãúu (R1) vaì giaí sæí O1 = O2, hai truûc (O1z1) vaì (O2z2)
truìng nhau.
z1= z
2
x1
O1 = O2
y1
θ
θ
2
R/R1
Ω
G
x2
Vectå quay cuía hãû quy chiãúu (R2) âäúi våïi hãû quy chiãúu (R1) :
R2/R1 1
.z
e
θ
Ω=
G
G
)
Trong âoï :
12 12
(, )(,
xx yy
OO OO
θ
==
JJJGJJJG JJJGJJJG y2
b) Træåìng håüp täøng quaït :
Trong træåìng håüp täøng quaït, chuyãøn âäüng tæång âäúi cuía hãû (R2)
cuía so våïi hãû (R1) coï thãø xem laì håüp cuía hai chuyãøn âäüng :
• Chuyãøn âäüng tënh tiãún våïi váûn täúc : 12
2/1
/1
()
R
R
dOO
vO dt
⎛⎞
=⎜⎟
⎝⎠
J
JJJJG
G
• Chuyãøn âäüng quay våïi vectå quay ΩR2/R1
G
coï phæång chiãöu thay âäøi theo thåìi gian.
2) Âaûo haìm cuía mäüt vectå trong hãû (R1) vaì trong hãû (R2):
G
Xeït mäüt veïctå Ut phuû thuäüc vaìo thåìi gian t vaì âæåüc mä taí trong cå såí (,
() 222
,)
xyz
eee
G
GG cuía hãû (R2)
nhæ sau : 22 22 22
() . . .
x
xyyz
Ut U e U e U e=++
z
G
GGG
G
Âaûo haìm cuía Ut trong hãû (R2) :
() 2
22
22
/2
..
y
xz
2
.
x
yz
R
dU
dU dU dU
ee
dt dt dt dt
⎛⎞
=++
⎜⎟
⎝⎠ e
G
G
GG
Âaûo haìm cuía Ut trong hãû (R1) :
()
G
2/ 1
/1 /2
RR
RR
dU dU U
dt dt
⎛⎞ ⎛⎞
=
+Ω ×
⎜⎟ ⎜⎟
⎝⎠ ⎝⎠
G
G
G
G
3) Håüp váûn täúc :
Xeït hãû quy chiãúu (R2) chuyãøn âäüng tæång âäúi so våïi hãû quy chiãúu (R ). Xeït mäüt âiãøm M chuyãøn
âäüng våïi váûn täúc
1
/2
()
R
vM
G trong hãû quy chiãúu (R2):
2
2
2
/
/
()
R
R
dO M
vM dt
⎛⎞
=⎜⎟
⎝⎠
J
JJJJG
G vaì chuyãøn âäüng våïi
váûn täúc /1
()
R
vM
G trong hãû quy chiãúu (R1) :
1
1
1
/
/
()
R
R
dOM
vM dt
⎛⎞
=⎜⎟
⎝⎠
J
JJJJG
G
Âënh lyï håüp váûn täúc : /1 /2
() () ()
R
eR
vM v M vM=+
GGG
Trong âoï : 2/1 2/1 2
() ()
eRRR
vM vO OM=+Ω×
J
JJJJG
G
GG
; 1
1
12
2/
/
()
R
R
dOO
vO dt
⎛⎞
=⎜⎟
⎝⎠
J
JJJJG
G
()
e
vM
G âæåüc goüi laì váûn täúc theo cuía âiãøm M.
4
Baìi giaíng Cå hoüc âaûi cæång (Meï canique Geïneïrale) PFIEV Âaì nàông
Váûn täúc theo cuía âiãøm M, taûi thåìi âiãøm âang xeït, chênh laì váûn täúc trong hãû (R1) cuía âiãøm
M* gàõn liãön våïi hãû (R2) vaì taûi thåìi âiãøm âang xeït M* truìng våïi âiãøm M. M* goüi laì truìng âiãøm
cuía M taûi thåìi âiãøm noïi trãn :
()
e
vM
G
/1
() (*)
eR
vM vM
=
G
G
4) Håüp gia täúc :
Xeït hãû quy chiãúu (R2) chuyãøn âäüng tæång âäúi so våïi hãû quy chiãúu (R1). Xeït mäüt âiãøm M chuyãøn
âäüng trong hãû quy chiãúu (R2) våïi gia täúc /2
()
R
aM
G
vaì trong hãû quy chiãúu (R1) våïi gia täúc
/1
()
R
aM
G.
Âënh lyï håüp gia täúc : /1 /2
() () () ()
R
eC
aM a M a M aM=+ +
GGGG
R
Trong âoï : 2/ 1
21 2 2/1 2/1 2
/1
() () (
RR
eR RRRR
R
d
a M aO OM OM
dt
⎛⎞
Ω
=+ ×+Ω×Ω×
⎜⎟
⎝⎠ )
G
J
JJJJG JJJJJG
G
G
GG
()
e
aM
G âæåüc goüi laì gia täúc theo cuía âiãøm M.
Gia täúc theo cuía âiãøm M, taûi thåìi âiãøm âang xeït, chênh laì gia täúc trong hãû (R1) cuía truìng
âiãøm M* cuía âiãøm M taûi thåìi âiãøm noïi trãn : aM
()
e
aM
G
/1
() (*)
eR
aM
=
G
G
R
Vaì : 2/ 1 / 2
()2 ()
CRR
aM vM=Ω ×
G
GG
()
C
aM
G âæåüc goüi laì gia täúc Coriolis cuía âiãøm M.
5) Caïc træåìng håüp chuyãøn âäüng âàûc biãût cuía (R2) âäúi våïi (R1):
a) Hãû (R2) chuyãøn âäüng tënh tiãún âäúi våïi hãû (R1) :
G
y2
y1
O1 = O2
2
θ
θ
R2/R1
Ω
G
H M = M*
x2
z1= z
Ta coï : 2/ 1 0
RR
Ω=
2/1
() ()
eR
vM vO=
GG
Do âoï :
2/1
() ()
eR
aM aO=
GG
()0
C
aM=
G
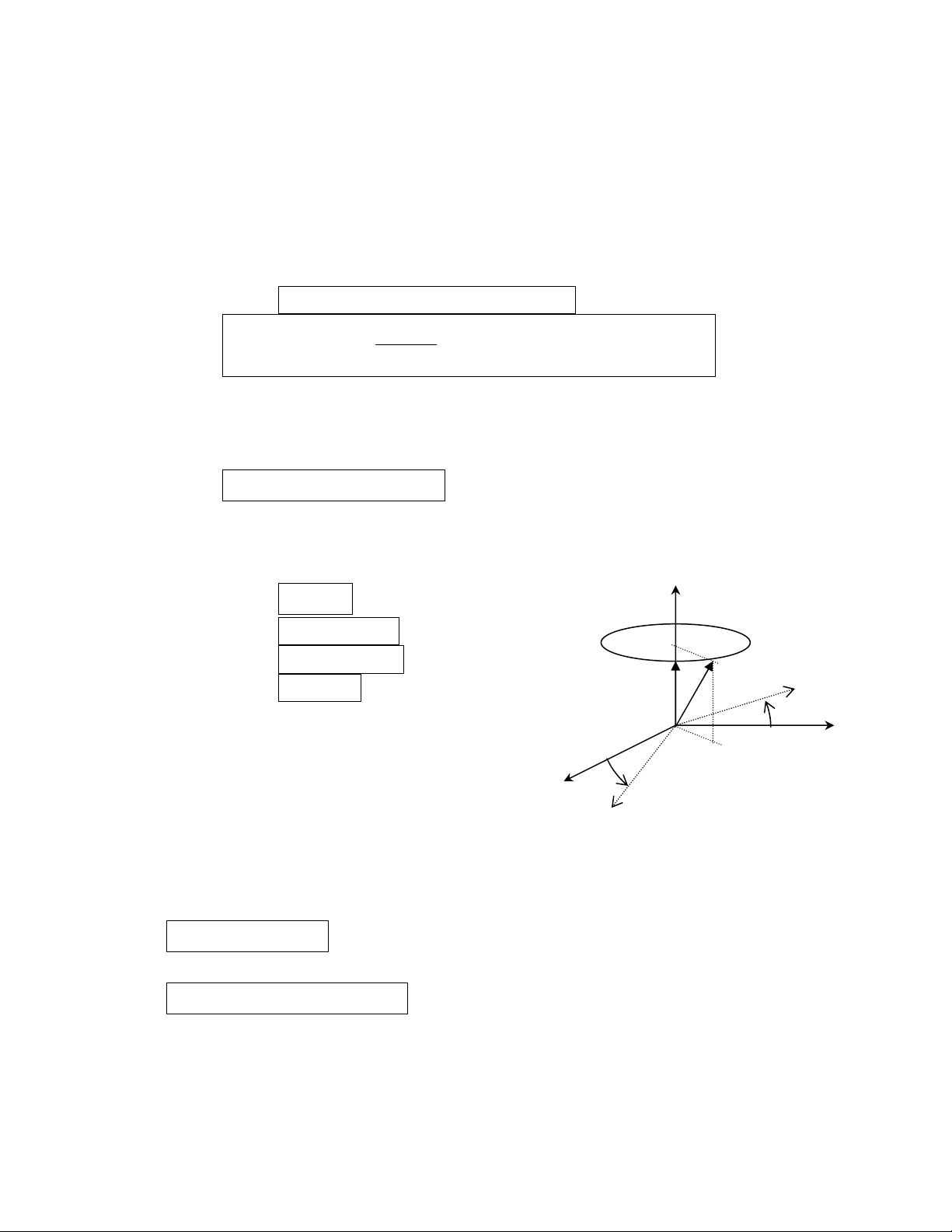
b) Hãû (R2) quay quanh mäüt truûc cäú âënh cuía (R1) :
Giaí sæí hãû quy chiãúu (R2) quay xung quanh truûc cäú
âënh (O1z1) cuía hãû quy chiãúu (R1) vaì giaí sæí O1 = O2,
hai truûc (O1z1) vaì (O2z2) truìng nhau.
x1
Vectå quay cuía hãû quy chiãúu (R2) âäúi våïi hãû quy
chiãúu (R1) : R2/R1 1
.z
e
θ
Ω=
G
G
Trong træåìng håüp naìy, ta coï :
2/1
() 0
R
vO =
G (do O2 cäú âënh trong R1)
1
() .
ez
vM e HM
θ
=×
JJJJG
GG
2/1
() 0
R
aO =
G (do O2 cäú âënh trong R1)
2
1
() . .
ez
aM e HM HM
θθ
=×−
JJJJG JJJJG
GG
Trong âoï : H laì hçnh chiãúu cuía M trãn truûc quay Oz1 = Oz2 .
•Ghi chuï : Gia täúc gäöm hai thaình pháön : Thaình pháön
()
e
aM
G
1
.z
aeH
τ
θ
=×
JJJJG
M
G
G
vuäng goïc våïi
HM (gia täúc tiãúp tuyãún) vaì thaình pháön 2.
n
aH
θ
=− M
J
JJJG
G
hæåïng tæì M vãö H (gia täúc hæåïng tám).
5