1
UBND HUYỆN LẠC SƠN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM HỌC SINH GIỎI CẤP HUYỆN
GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY CẤP THCS
NĂM HỌC 2012 – 2013
C¸c chó ý:
1. NÕu trong ®Ò yªu cÇu tãm t¾t c¸ch gi¶i nhng häc sinh chØ cho kÕt qu¶ ®óng víi ®¸p
¸n th× cho một nửa điểm của phần đó
2. Trêng hîp häc sinh gi¶i theo c¸ch kh¸c:
- NÕu ra kÕt qu¶ kh«ng ®óng víi ®¸p ¸n th× kh«ng cho ®iÓm.
- NÕu ra kÕt qu¶ ®óng víi ®¸p ¸n th× gi¸m kh¶o kiÓm tra cô thÓ tõng bíc, nếu các
bước đúng thì cho điểm tối đa
3. Nếu học sinh không làm tròn theo quy ước là 5 chữ số thì trừ đi 1 điểm của bài đó
Đề bài và tóm tắt lời giải Ghi kết
quả
Câu 1: (5 ®iÓm): Mỗi phần đúng cho 2.5 điểm
a, Tính 33
3
33
326
21
18
21
54
2126200
B
b) Tính D và viết dưới dạng phân số tối giản
4
D=5+ 4
6+ 4
7+
4
8+
4
9+
10
a, B = 8
b, D =
1209
6785
Câu
2
(
5 đi
ểm)
Ph
ần 1 cho 3 điểm, phần 2 cho 2
đi
ểm
.
1, Cho a = 11994; b = 153923; c = 129935.
a,Tìm ƯCLN( a, b, c) b,Tìm BCNN( a, b, c)
2, Tìm 3 chữ số cuối cùng bên phải của 2012
7
Lời giải tóm tắt:
1, a, Áp dụng quy tắc tìm ước cơ bản tìm được ƯCLN (a,b) = 1999;
ƯCLN(a,b,c) = 1999
b, BCNN (a,b) = 923538; BCNN(a,b,c) = 60029970
2,
)1000(mod2014924917777)1000(mod0017
)1000(mod0017);1000(mod001)249()1000(mod001249
);1000(mod249)7(7);1000(mod2497
210200020122000
100522
10101010010
xxxx
1, a
ƯCLN( a, b, c)
= 1999
b,
BCNN( a, b, c)
= 60029970
2,
3 chữ số cuối
cùng bên phải
là: 201
2
Câu 3: (5 điểm) Phần 1 cho 1 điểm, phần 2 cho 2 điểm, phần 3 cho 2 điểm
Cho đa thức: 260228418)( 234 xxxxxP
1, Hãy tìm số dư trong phép chia P(x) cho đa thức 2x + 5
2, Hãy tìm m để đa thức
P(x)
+ m
3
2 chia hết cho đa thức 2x - 7
3, Hãy tìm các nghiệm của đa thức P(x)
Lời giải tóm tắt:
1, Áp dụng định lý Bozu ta có dư của phép chia đa thức P(x) cho 2x + 5 là P(
2
5
).
Ấn trên máy ta được số dư bằng: -402,1875
2, Để đa thức
P(x)
+ m
3
2 chia hết cho 2x - 7 thì
P(x)
+ m
3
2 = (2x - 7 ). Q(x)
P(
2
7) + m
3
2 = 0 .
m
= - P(
2
7) :
3
2 = -544,21875
3, Dễ thấy P(x) có một nghiệm bằng -1(có thể KT bằng chức năng của phím sifht slove )
nên áp dụng lược đồ Hoocne ta có:
P(x) = (x+1)(x3-9x2-32x+260). Dùng máy tính ta tính được các nghiệm còn lại của P(x)
1,
Số dư trong
phép chia
P(x) cho đa
thức 2x + 5
-402,1875
2,
m =-
544,21875
3,
x1= -1
x2= 5
x3= 9,48331
x4= -5,48331
Câu 4: (5 điểm) Phần 1 cho 3 điểm, phần 2 cho 2 điểm
Cho đa thức: 4 3 2
P(x)=x +ax +bx +cx+d
Biết P(1) = 1; P(2) = 4; P(3) = 7; P(4) = 10
1, Tìm các hệ số a, b ,c, d
2, Với a, b,c,d vừa tìm được ta chia đa thức
P(x)
cho 2x+3 ta được thương là
đa thức Q(x) có bậc là 3. Hãy tìm hệ số của x trong Q(x)?
Lời giải tóm tắt:
1, Đặt B(x) = 3x-2. Ta có B(1)=1; B(2)=4; B(3)=7; B(4)=10
=> P(x)-B(x) có 4 nghiệm 1; 2; 3; 4 và là đa thức bậc 4 có hệ số cao nhất bằng 1
=> P(x)-B(x)= (x-1)(x-2)(x-3)(x-4)
=> P(x)= (x-1)(x-2)(x-3)(x-4)+B(x)
=> P(x) = (x-1)(x-2)(x-3)(x-4)+3x-2
=> P(x)=x4-10x3+35x2-47x+22
2, Áp dụng lược đồ Hoocne viết :
P(x) = (2x+3)(
16
3361
)
16
1003
8
209
4
23
2
1223 xxx
1,
a = -10
b = 35
c = - 47
d = 22
2,
Hệ số của x trong
Q(x) là:
8
209
Câu 5: (5 điểm) Phần 1 cho 3 điểm, phần 2 cho 2 điểm
1, A = -0,55729
3
1, Cho sinx =
3
5
0 90
o o
x Tính A =
xx
xxx
cot6tan5
tan32sin5cos2
2
22
2, Tìm phân số tối giản sinh ra số thập phân vô hạn tuần hoàn: 621,12(2012)
2, Phân số cần
tìm là:
9999
6210599
Câu 6: (5 điểm)Phần 1 cho 3 điểm, phần 2 cho 2 điểm
Một người tiết kiệm tiền để mua một chiếc xe máy bằng cách hàng tháng gửi
vào ngân hàng a đồng . Biết rằng lãi xuất của ngân hàng là 0.8%/tháng, hàng
tháng không rút lãi ra.
1, Xây dựng công thức tính tổng số tiền tiết kiệm có được sau n tháng?
2, Đúng ba năm sau người đó mua được chiếc một xe máy trị giá 20600000
đồng . Hỏi hàng tháng người đó phải gửi vào ngân hàng một số tiền là bao
nhiêu?
Lời giải tóm tắt:
1, Gọi số tiền nhận được sau tháng thứ n là Tn. Số tiền gửi hàng tháng là
a(đồng). Lãi suất hàng tháng là m (%)
Sau 1 tháng số tiền cả gốc và lãi là: T1= a+am = a(1+m)
Đầu tháng thứ 2 số tiền là: a(1+m) + a = a(1+m+1)=
1)1( 2 m
m
a
Sau 2 tháng số tiền cả gốc và lãi là: T2=
1)1( 2 m
m
a+
1)1( 2 m
m
am
=
1)1( 2 m
m
a.(1+m)
Đầu tháng thứ 3 số tiền là:
1)1( 2 m
m
a (1+m)+ a = a (
m
mm )1(1)1( 2 +1)
=
1)1( 3 m
m
a
Sau 3 tháng số tiền cả gốc và lãi là: T2=
1)1( 3 m
m
a.(1+m)
.....................
Sau n tháng số tiền cả gốc và lãi là:
mm
m
a
Tn
n 111 (*)
2, Từ (*) suy ra a =
)1(1)1(
.
mm
mT
n
n
. Thay Tn=20600000, m=0,8 %= 0,008;
n = 36. Vậy sau 3 năm ( 36 tháng) để có 20600000 đồng thì hàng tháng người
1, Công thức tổng số
tiền có được sau n
tháng
mm
m
a
Tn
n 111
2, Số tiền phải gửi
hàng tháng là:
492105,3(đồng)
4
đó phải gửi vào ngân hàng số tiền là:a =
)008,01(1)008,01(
008,0.20600000
36 = 492105,3
Câu 7: (5 điểm)
Tìm số tự nhiên n ( 20349 < n < 47238 ) và A để A = 4789655 - 27n là lập
phương của một số tự nhiên .
Lời giải tóm tắt:
Đặt X= 3274789655 n với 20349 < n < 47238 suy ra X3 = A có
3514229 < 4789655 - 27n < 4240232 hay 351429 < X3 < 4240232
tức là 152,034921 < X < 161,8563987. Do X là số tự nhiên nên X chỉ có thể
bằng một trong các số sau : 153; 154; 155; ...; 160; 161.
Vì X= 3274789655 n nên n =
27
X4789655 3
. Ghi công thức tính n trên
máy : 153 → X X=X+1:
27
X4789655 3
cho đến khi nhận được các giá trị
nguyên tương ứng được X =158 suy ra A=393944312
n =31309
A= 393944312
Câu 8: (5 điểm) Phần 1 cho 2 điểm, phần 2; 3 mỗi phần 1,5 điểm
Cho dãy số với số hạng tổng quát được cho bởi công thức
52
)51()51( nn
n
U
với n = 1 , 2 , 3 , . . . k , . . .
1. Tính U1, U2, U3, U4, U5.
2. Lập công thức truy hồi để tính Un+2 theo Un+1 , Un .
3. Lập quy trình ấn phím liên tục tính Un+2 .
Lời giải tóm tắt:
1, Nhập biểu thức Un vào máy và thay các giá trị của n = 1,2,3,4,5 ta được 5
số hạng đầu của dãy
2, Công thức truy hồi có dạng; Un+2 =aUn+1+ b Un + c. Ta có hệ
U3 = aU2+bU1+ c -2a+b+c=8
U4 = aU3+bU2+ c
8a-2b+c=-24
U5 = aU4+bU3+ c -24a+8b+c=80
Giải hệ ta được : a = -2, b = 4, c = 0
Vậy: Un+2 =-2Un+1 +4Un
3, 1
SHIFT
STO
A
-2
SHIFT
STO
B
ANPHA
A
ANPHA
=
-2
ANPHA
B
+
4
ANPHA
A
ANPHA
:
1,
U1= 1
U2 = -2
U3 = 8
U4= -24
U5.= 80
2,
Un+2 =-2Un+1
+4Un
5
----------------------------------Hết-----------------------------------
ANPHA
B
ANPHA
=
-2
ANPHA
A
+
4
ANPHA
B
Lặp dấu bằng
=
...
=
...
Câu 9: (5 điểm)Phần a cho 2 điểm, phần b cho 3 điểm
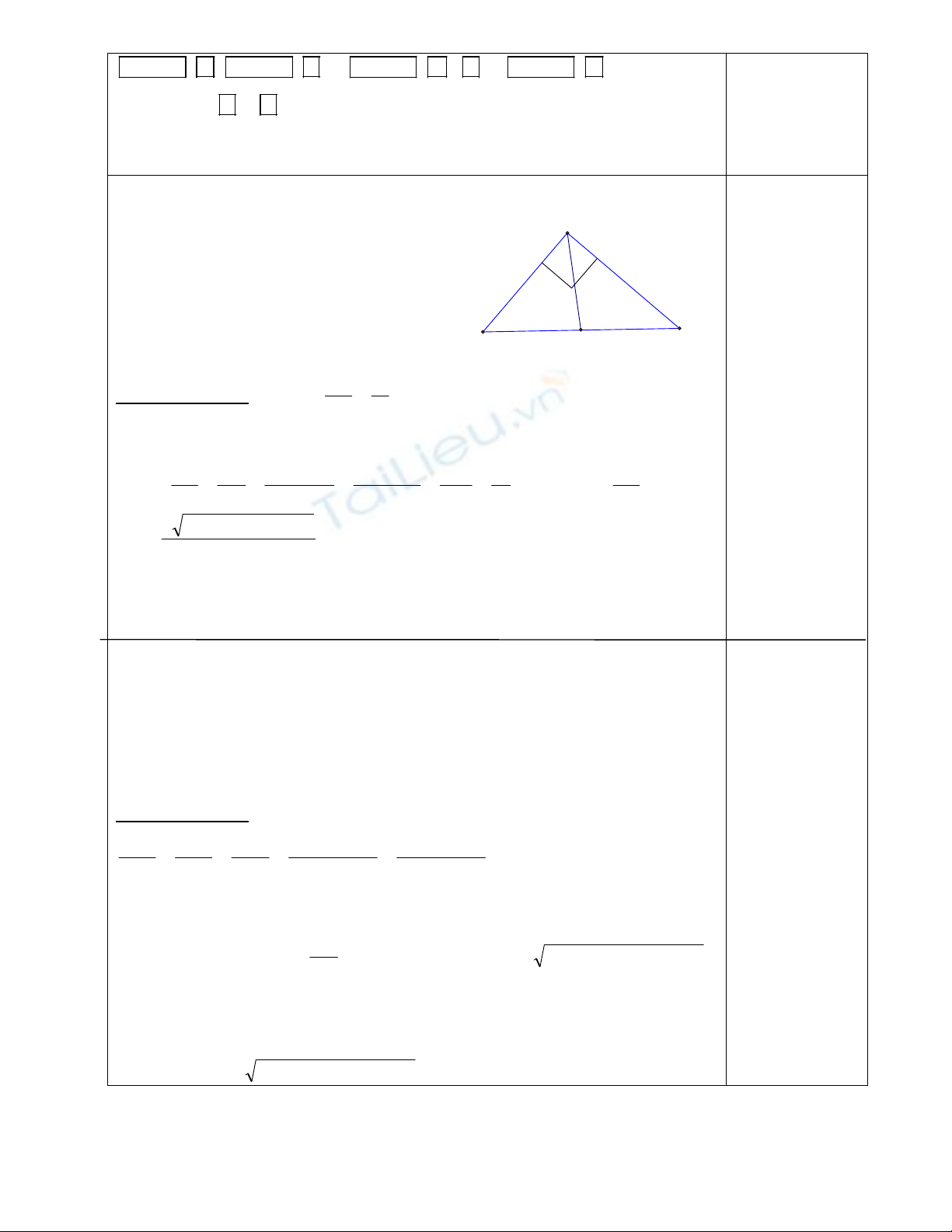
Cho
ABC
vuông tại A có BC = 2,55m;
các cạnh AB và AC tỉ lệ với 8 và 15,
AD là phân giác trong của góc A.
a, Tính góc B, góc C
b, Tính chu vi của tam giác ABD
Lời giải tóm tắt:a,
15
8
tan
AC
AB
C; góc C =2804'21''; góc B= 61055'39''
b, AC=BC.sin61055'39'' = 2,25m; AB=BC.8:15=1,2m
Ta có 23
17
45,3
55,2
ACAB
BC
ACAB
DCBD
AC
DC
AB
BD suy ra BD =
115
102 m
AD =
AC
AB
)C(..2
BppACAB
Tính chu vi của tam giác ABD là: BD+AD+AB= 3,19373m
Câu 10: (5 điểm) Phần a cho 3 điểm, phần b cho 2 điểm
Cho tam giác ABC có góc A bằng 450, góc B bằng 590, AB – BC = 12cm.
a, Tính độ dài các cạnh của tam giác ABC ?
b, Tính bán kính đường tròn ngoại tiếp tam giác ABC.
Lời giải tóm tắt:a,Góc C = 760. Áp dụng định lí hàm số Sin ta có
A
C
A
C
BCAB
C
AB
AC
A
BC
sin
sin
12
sin
sin
sin
sin
sin
suy ra AB = 44,24027cm; AC =39,08222cm ; BC =32,24027cm
b, Áp dụng công thức S=
abc
4
và công thức Hêrông S= ))()(( cpbpapp
(S là diện tích của tam giác ABC, a,b,c là độ dài các cạnh, R là bán kính đường
tròn ngoại tiếp tam giác, p là nửa chu vi của tam giác)
suy ra R= abc:(4 ))()(( cpbpapp )= 22,79731cm
a,
Góc B=
61055'39''
Góc C
= 2804'21''
b,
Chu vi của tam
giác ABD là:
3,19373m
a,
AB = 44,24027cm;
AC =39,08222cm
BC =32,24027cm
b, Bán kính đường
tròn ngoại tiếp tam
giác ABC là:
22,79731cm
DC
B
A