WWW.VNMATH.COM
ĐÁP ÁN THANG ĐIỂM THI THỬ ĐẠI HỌC MÔN TOÁN KHỐI B LẦN I
NĂM HỌC 2013-2014
Câu
NỘI DUNG Điểm
I 1.Khi m=1
Khảo sát và vẽ đồ thị hàm số
3 2
3
y x x
1
a)TXĐ:D=R
b)Sự biến thiên
-Chiều biến thiên 2
0
' 3 6 ' 0
2
x
y x x y x
………………………………………………………………………………………...
Hàm số đồng biến trên khoảng

và
(2; )

Hàm số nghịch biến trên khoảng
(0;2)
-Cực trị : Hàm số đạt cực đại tại
0 ;y 0
cd
x
Hàm số đạt cực tiểu tại
2 ;y 4
ct
x
-Giới hạn : lim ; lim
 
 
x x
………………………………………………………………………………………...
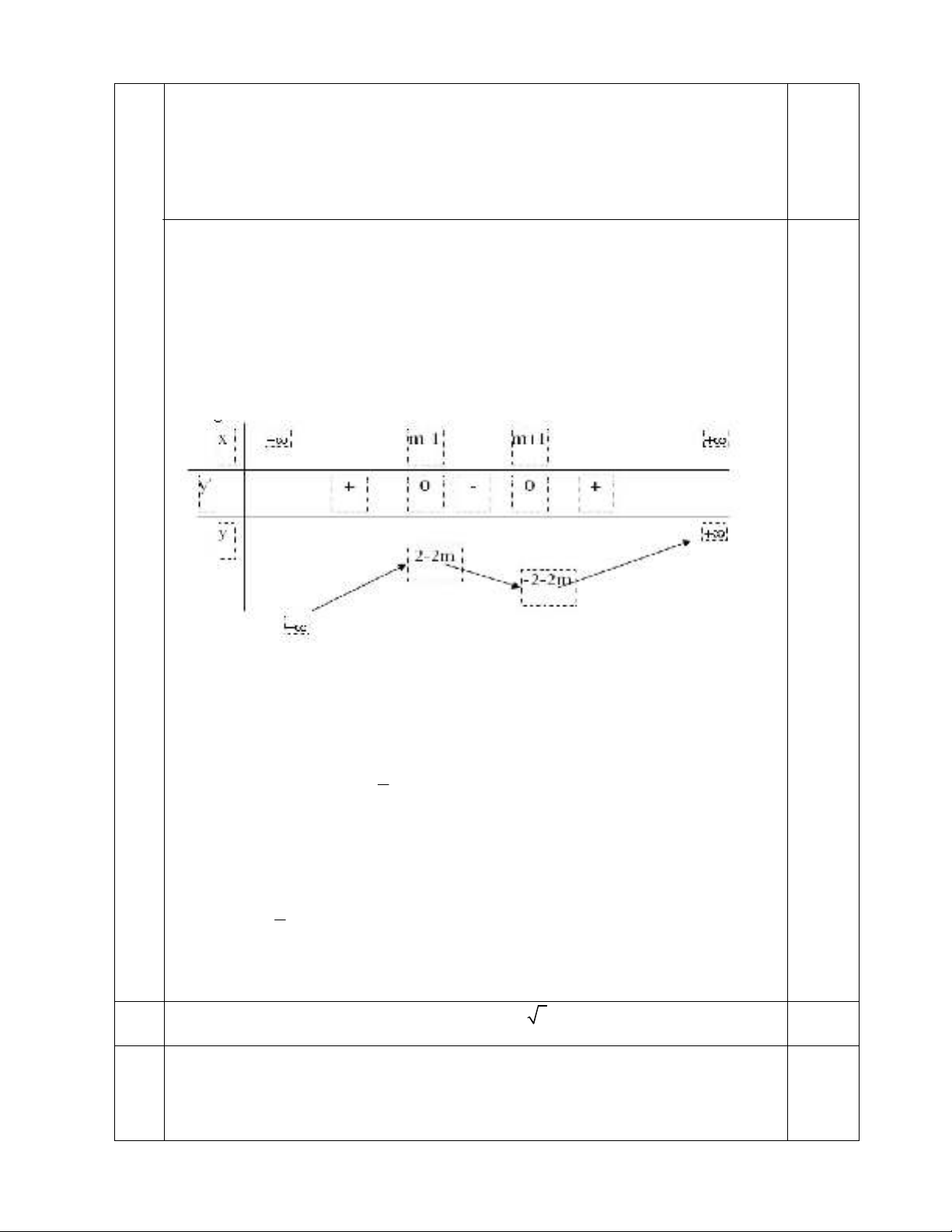
Bảng biến thiên
………………………………………………………………………………………...
Đồ thị
0.25
0.25
0.25
0.25
y'
+
+
x
y


-


0
0
0
2
0
-
4
WWW.VNMATH.COM
2:Tìm m để đồ thị hàm số cóđiểm cực đại , điểm cực tiểu và khoảng cách từ điểm
cực tiểu của đồ thị hàm số đến gốc toạ độ O bằng 3 lần khoảng cách từ điểm cực đại
của đồ thị hàm số đến gốc toạ độ O
TXD: D=R
Ta có 2 2
' 3 6 3( 1)
y x mx m
Đồ thị hàm số có điểm cực đại ,điểm cực tiểu khi và chỉ khi
' 0
y
có hai nghiệm
phân biệt và đổi dấu khi đi qua các nghiệm
2 2
3 6 3( 1) 0
x mx m
có hai nghiệm phân biệt
2 2
' 9m 9( 1) 9 0 m
m
Vậy
m
đồ thị hàm số có điểm cực đại ,điểm cực tiểu và
1
' 0
1
x m
yx m
Điểm A(m-1;2-2m);B(1+m,-2-2m) lần lượt là điểm cực đại ,điểm cực tiểu của đồ thị
hàm số theo giả thiết ta có OB=3 OA
2 2 2 2 2 2
9 (m+1) ( 2 2 ) (m-1) (2 2 )
OB OA m m
2
2
2 5 2 0
1
2
m
m m m
Vậy với
m 2
1
m
2
thì đồ thị hàm số cóđiểm cực đại , điểm cực tiểu và khoảng cách từ
điểm cực tiểu của đồ thị hàm số đến gốc toạ độ O bằng 3 lần khoảng cách từ điểm cực
đại của đồ thị hàm số đến gốc toạ độ O
1
0.25
0.25
0.25
0.25
2
Giải phương trình : 2 2
2s inx(cos x sin x) sinx 3 cos3x
(1) 1
phương trình (1)
0.25
WWW.VNMATH.COM
2sin x.cos 2 x s inx 3 cos 3x sin 3x s inx sinx 3 cos 3x
1 3
sin 3x 3 cos 3x 2sin x sin 3x cos3x s inx
2 2
cos sin 3x sin cos3x sinx sin(3x ) sin x
3 3 3
3x x k2 x k
3 6
k Z
3x x k2 x k
3 3 2
3.Giải phương trình 2
4 6 2 13 17
x x x x
Điều kiện :
4x6
Ta có :
2 2
4 6 2 13 17 ( 4 1) ( 6 1) 2 x 13 15 0
( 4 1)( 4 1) ( 6 1)( 6 1) ( 5)(2 3) 0
4 1 6 1
x x x x x x x
x x x x x x
x x
5 5
( 5)(2 3) 0
4 1 6 1
x x x x
x x
5
1 1
(2 3) 0
4 1 6 1
x
x
x x
Ta có 1 1 1 1
(2 3) 0 (2 3)
4 1 6 1 4 1 6 1
x x
x x x x
Vì
1 1 1
1 4;6
4 1 6 1 4 1 x
x x x
và
2 3 5 4;6
x x
Vậy phương trình đã cho có nghiệm duy nhất x= 5
0.25
0.25
0.25
1
0.25
0.25
0.25
0.25
4 Tính tích phân
3
2
2
ln 2 ( 3) dx
I x x
1
Ta có
3 3 3
2 3 2
2 2 2
3 3 3 3
2
2 2 2 2
ln 2 ( 3) dx ln( 3 2) ln( 1) ( 2)dx
ln( 1) dx ln( 2)dx 2 ln( 1)dx ln( 2)dx
I x x x x dx x x
x x x x
Xét
3
2
J 2 ln(x 1) dx
Đặt
2dx
u 2ln(x 1) du
x 1
dv dx
v x 1
3
3 3 3
2 2 2
2
J 2(x 1).ln(x-1) 2 dx 2(x 1).ln(x-1) 2x. 4ln 2 2
0.25
0.25
0.25
WWW.VNMATH.COM
Xét
3
2
K ln(x 2)dx
Đặt
dx
u ln(x 2) du
x 2
dv dx
v x 2
3
3 3 3
2 2 2
2
K (x 2).ln(x+2) dx (x 2).ln(x+2) x. 5ln5 4ln 4 1
vậy
5ln 5 4ln 2 3
I
0.25
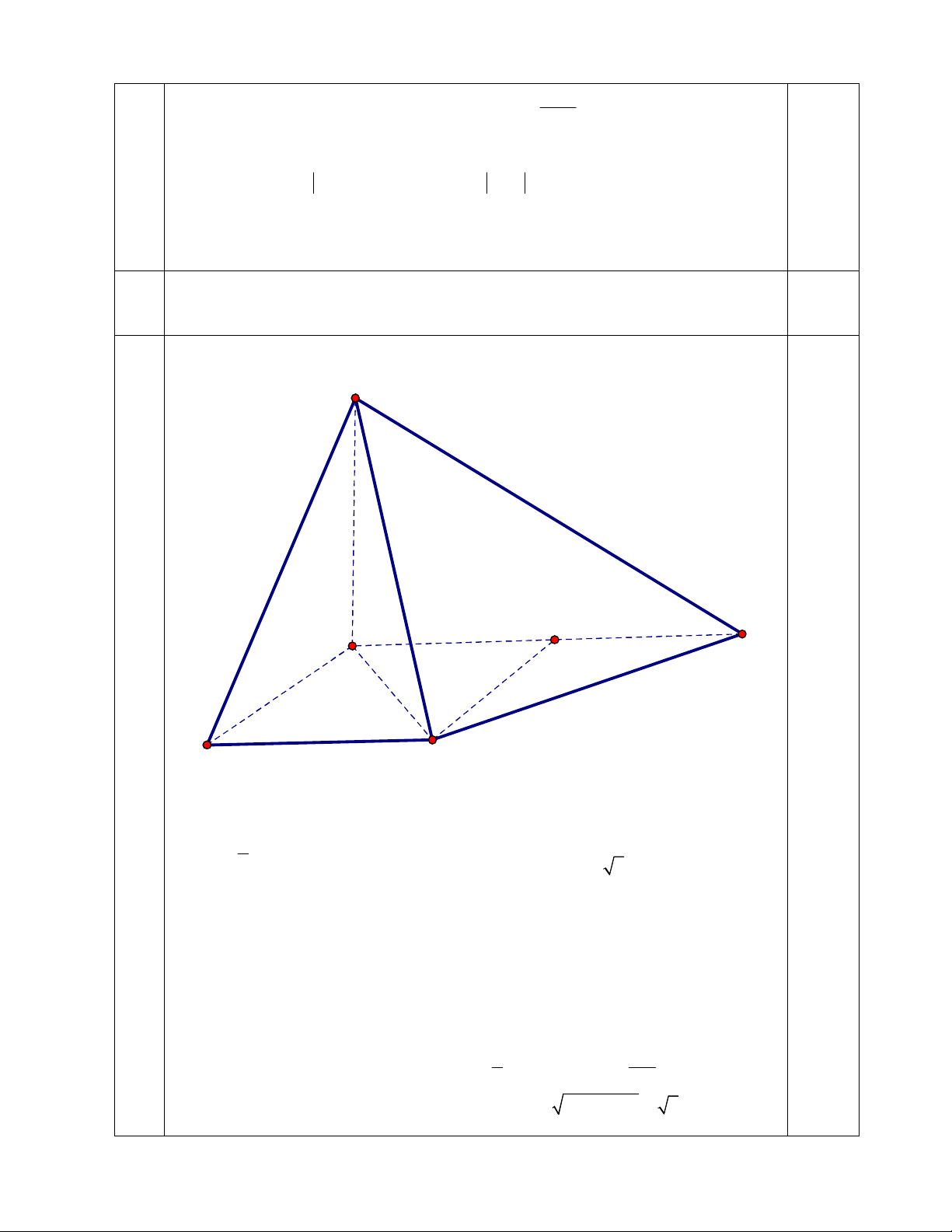
5 Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, D biết
AB =2a ; AD=DC=a.(a>0)
SA (ABCD)
,góc giữa hai mặt phẳng (SBC) và (ABCD)
bằng 45 0 Tính thể tích khối chóp SABCD và khoảng cách từ B tới mặt phẳng (SCD)
1
A
D
C
B
S
H
+Theo giả thiết ta có AD= DC = a .Gọi H là trung điểm của AB
HA=HB=a Từ giả
thiết
ADCH là hình vuông cạnh a .Trong tam giác
ABC
có CH là trung tuyến
và 1
CH AB
2
ABC
vuông cân tại C AC BC
AC BC a 2
vì
BC AC
BC (SAC) BC SC
BC SA
+Có
0
(SBC) (ABCD) BC
BC SC (SBC)
SCA 45
BC AC (ABCD)
SA (ABCD)
là góc giữa (SBC) và (ABCD)
+Ta có diện tích hình thang
2
1 3
( ).
2 2
ABCD
a
S AB DC AD
+Có tam giác
ΔSAC
vuông cân tại A ta có 2 2
SA=AC= AD +DC 2
a
0.25
0.25
WWW.VNMATH.COM
+Thể Tích khối chóp SABC là :
2
3
S.ABCD ABCD
1 1 3a 2
V S .SA a 2. a
3 3 2 2
Ta có
SDCB
SDCB BCD
BCD
3V
1
V S .d(B;(SCD)) d(B;(SCD))
3 S
Trong
BCD
có
0
C 135
nên
0 3
SDCB
1 1 2
V BC.CD.sin135 .SA a
3 2 6
Vậy
33
SDCB
2
0
BCD
2
3. a
3V
2a a 6
6
d(B;(SCD)) 1
S 3
3a
a.a 2.sin135
2
0.25
0.25
câu6 Cho x,y là các số thực và thoả mãn x,y >1 .Tìm giá trị lớn nhất của biểu thức
:
3 3 2 2
( ) ( )
( 1)( 1)
x y x y
Px y
1
Đặt t =x + y điều kiện t > 2
Áp dụng bất đẳng thức
2
4 ( )
xy x y
ta có
2
t
xy
4
3 2
(3 2)
1
t t xy t
Pxy t do 3t-2>0
2
t
xy
4
nên ta có
2
3 2
2
2
(3 2)
4
2
1
4
t
t t t
t
Pt
t
t
Xét hàm số
2
( )
2
t
f t
t
trên
(2; )

có
2
2
0 (l)
4
'( ) '( ) 0
4 (tm)
( 2)
t
t t
f t f t t
t
x
x 2
lim f(t) ; lim f (t)


0.25
0.25
0.25
0.25
f'(t)
t
f(t)
2

0


+ -
4
8