y
’
x
y
’
1
_
3
3
x
Câu Ý Nội dung Điểm
I 1 a. Tập xác định:
\ 2
D R 0.25
b. Sự biến thiên
Chiều biến thiên:
'
2
3
1
yx
y’<0 với x
D
; y’ không xác định khi x =1
Suy ra hàm số nghịch biến trên các khoảng
( ;1)

và
1;

Cực trị : Hàm số không có cực trị
0.5
Tiệm cận : 1 1 1 1
3 3
lim lim ;lim lim
1 1
x x x x
x x
y y
x x
 
Suy ra đồ thị có một tiệm cận đứng là đường x = 1
3
lim lim 3
1
x x
x
y
x
Suy ra đồ thị có một tiệm cận ngang là đường y = 3
0.5
Bảng biến thiên:
0.25
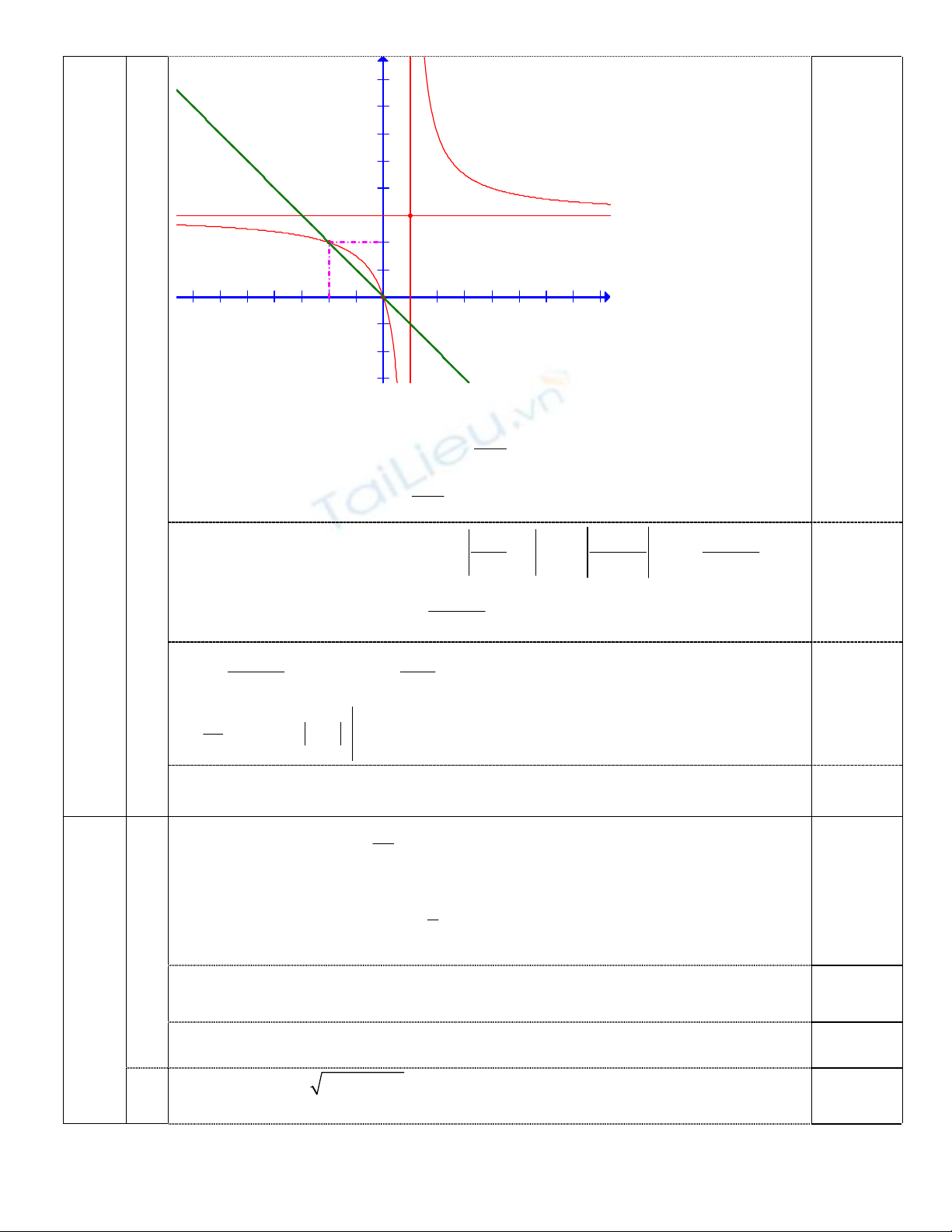
c. Đồ thị: Đồ thị đi qua gốc tọa độ; đi qua điểm (-2;2). Nhận giao của 2 đường
tiệm cận là điểm (1;3) làm tâm đối xứng của đồ thị
0.5
ĐÁP ÁN ĐỀ THI THỬ TỐT NGHIỆP THPT 2010
Đề số 1
Thời gian 180 phút
-7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8
-2
-1
1
2
3
4
5
6
7
8
x
y
O
2. Hoành độ Giao điểm của hàm số
3
1
x
y
x
và đường thẳng y = - x là nghiệm của
phương trinh: 2
0
30 2 0
2
1
x
xx x x xx
0.25
Diện tích hình phẳng cần tìm là:S = 0 0 0
2 2
2 2 2
3 2 2
1 1 1
x x x x x
xdx dx dx
x x x
(vì trên [-2;0] thì 22
2 0 2
0
1
1 0
x x x x
x
x
)
0.25
S = 0 0
2
2 2
2 3
3
1 1
x x
dx x dx
x x
0
2
2
3 3ln 1
2
xx x
0.25
4 3ln3
0.25
3x - 32-x – 8 = 0 9
3 8 0
3
x
x
Đặt 3x = t (t>0)
Phương trình đã cho có dạng: 9
8 0
t
t
t2 - 8t – 9 = 0
0.5
9
t
t
0.25
1
Với t = 9, ta có : 3x = 9
x = 2
Vậy phương trình đã cho có nghiệm là x = 2 0.25
II
2 Hàm số 2
2 3
y x x
xác định với mọi x
R
0.25
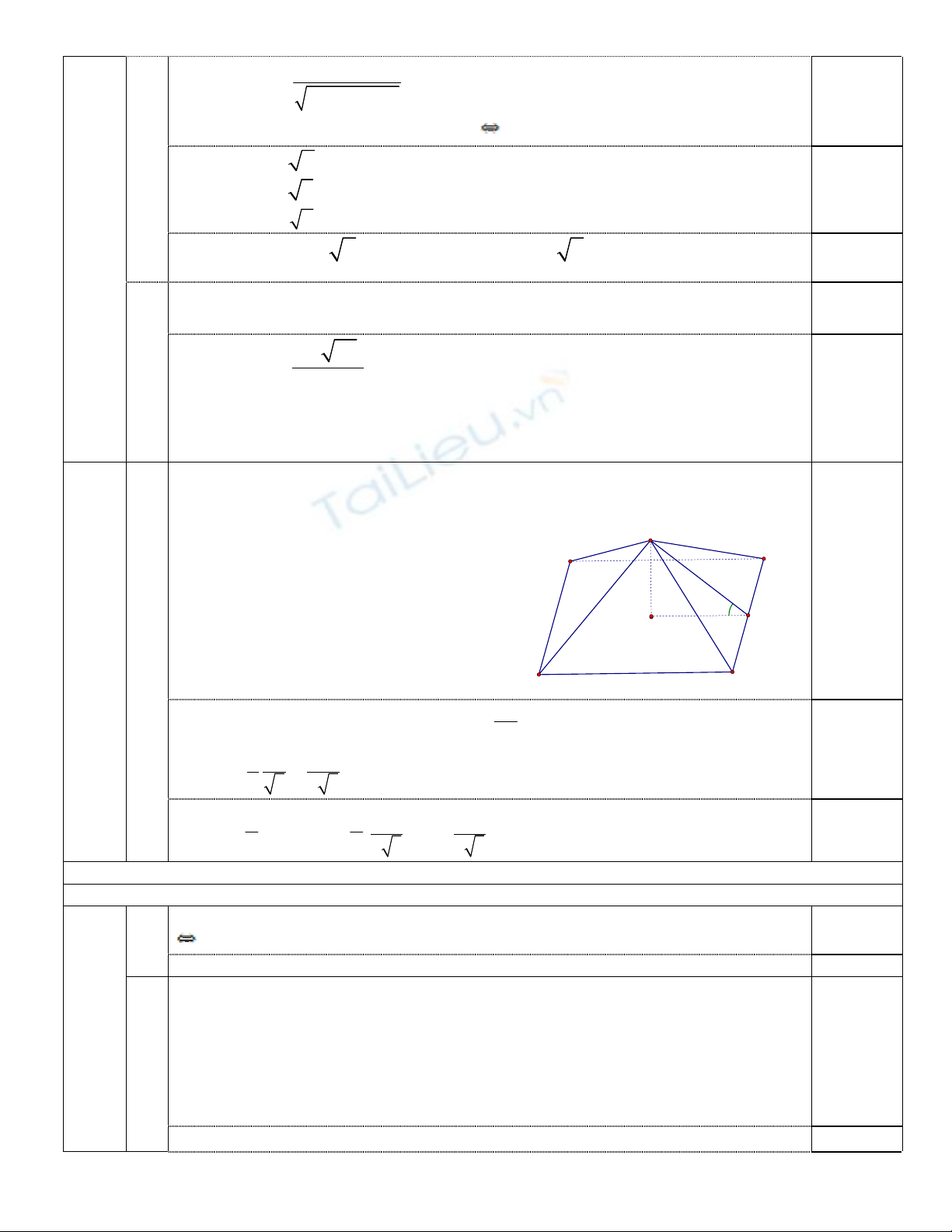
2
1
'
2 3
x
y
x x
trên đoạn
2;3
thì y’ = 0 x = -1
Ta có : y(-1)=
2
y(-2)=
3
y(3)=
3
2
0.5
2;3 2;3
min ( 1) 2 max (3) 3 2
y y y y
0.25
Ta có
2
1 40 39 39
i
0.5
3
Suy ra : 1,2
1 39
4
i
z
0.5
Gọi O là tâm hình vuông ABCD.
Do SABCD là hình chóp tứ giác đều
( )
SO ABCD
Gọi I là trung điểm BC
OI BC
SI BC
nên
SIO
là góc giữa mặt bên và mặt
đáy
0
30
SIO
0.5
Trong tam giác vuông SIO có: tan300 =
SO
OI
SO = OI. tan300
SO = 1
2
3 2 3
a a
0.25
III
VSABCD=
1
3
SO.SABCD=
1
3
2 3
a
a2 =
3
6 3
a
(đvtt) 0.25
B- Phần dành riêng:
Phần dành cho thí sinh ban Cơ Bản
x2 + y2 + z2 - 2x - 4y - 6z – 22 = 0
(x-1)2 + (y-2)2 + (z-3)2 = 36 0.5
1
Nên mặt cầu (S) có tâm I(1 ;2 ;3) và bán kính R= 6 0.5
Tọa độ giao điểm của đường thẳng (d) và mặt cầu (S) là nghiệm của hệ
2 2 2
1 2 3 36
1
2 2
3 2
x y z
x t
y t
z t
0.25
IVa
2
t2+(2t)2+(-2t)2=36
9t2 =36
2
t
0.25
300
S
a
I
O
DC
B
A
Với t=2
3
6
1
x
y
z
0.25
Với t=-2
1
2
7
x
y
z
Vậy (d) (S) tại 2 điểm : (3 ;6 ;-1) và (-1;-2;7)
0.25
Hoành độ giao điểm của 2
3
à
y x x v y x
là :
23x x x
2
0
4 0
4
x
x x x
0.25
Diện tích hình phẳng cần tìm là :
42
0
4
S x x dx
0.25
Va
4
43
2 2
00
32
( 4 ) (2 )
3 3
x
x x dx x
(đvdt) 0.5
Phần dành cho
thí sinh ban Nâng Cao
Đặt x = cost,
;
2 2
t
Đổi cận :
x
2
2
1
t
4
0
dx= d(cost)=-sint dt
0.25
1 0
2 2 4
2 2 2
0
224
.
1 x 1 cos t
. cos cos
sint sint
I d x sint dt dt
x t t
2 2
4 4 4 4
2 2 2
0 0 0 0
sin 1 cos 1
cos cos cos
t t
dt dt dt dt
ttt
0.5
IVb 1
=
4 4
0 0
tan
t t
= 1-
4
0.25
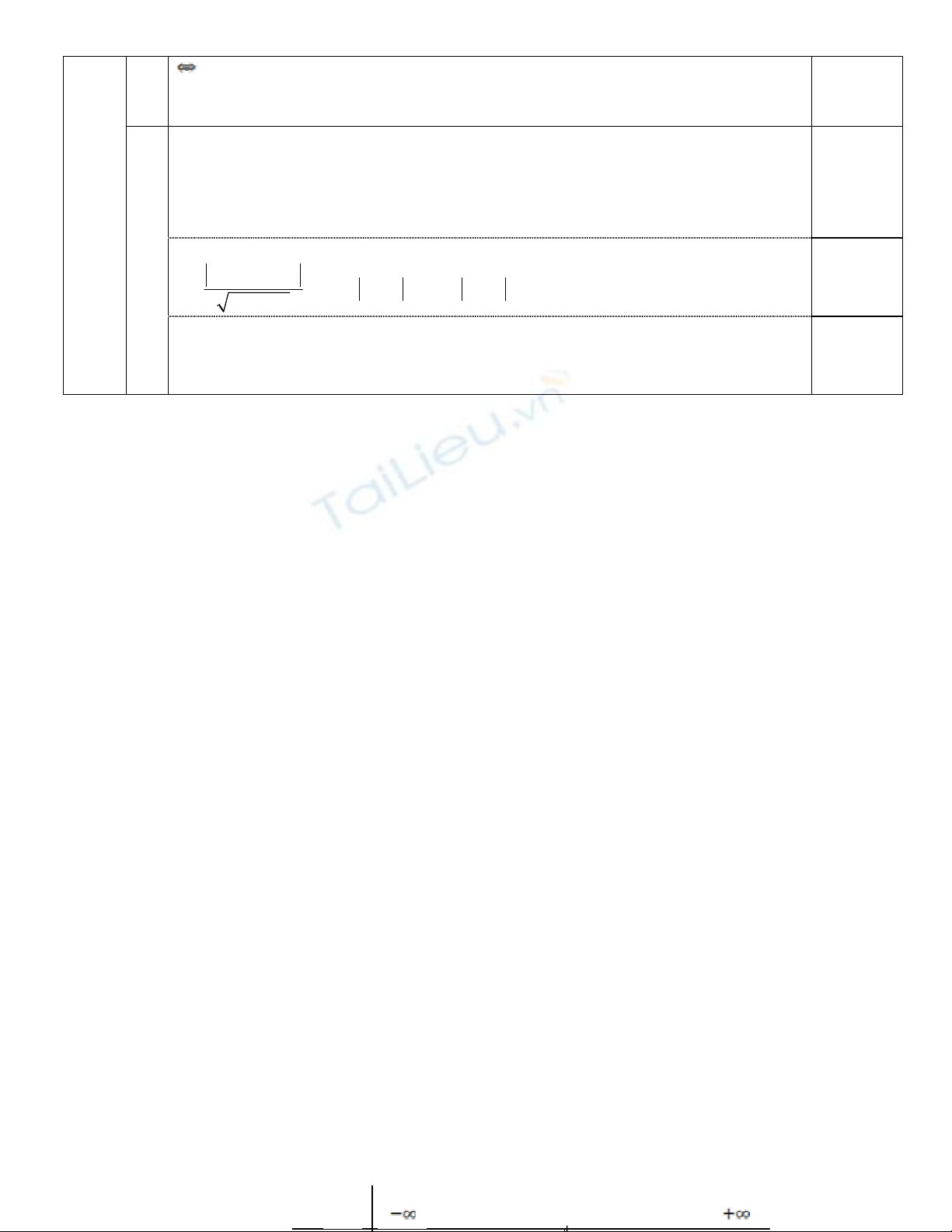
Vb 1 x2+y2+z2-2x+4y-6z+10=0 0.5
x
1
x
(x-1)2 +(y+2)2 +(z-3)2 =4
Suy ra (S) có tâm I(1 ;-2 ;3) và bán kính R= 2
1
v
d
=(-2; 2; 1);
2
v
d
=(2; -3; -2);
(P) // d1 và (P) // d2 nên 1 2
;
p d d
n v v
= (-1 ;-2 ;2)
Suy ra (P) có dạng : x + 2y - 2z + m = 0
0.5
Vì (P) tiếp xúc (S) nên khoảng cách từ tâm I(1 ;-2 ;3) đến (P) bằng R
1 4 6
1 4 4
m
=2
9 6 9 6
m m
0,5
2
15
3
m
m
Vậy (P) là: x + 2y - 2z + 15 = 0 hoặc x + 2y - 2z + 3 = 0.
0,5