1/4
BỘ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ CHÍNH THỨC
ĐÁP ÁN - THANG ĐIỂM
ĐỀ THI TUYỂN SINH ĐẠI HỌC, CAO ĐẲNG NĂM 2007
Môn: TOÁN, khối B
(Đáp án - Thang điểm gồm 04 trang)
Câu Ý Nội dung Điểm
I 2,00
1 Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1,00 điểm)
Khi m =1 ta có 32
yx3x4=− + − .
• Tập xác định: D = \.
• Sự biến thiên:
2
y' 3x 6x,=− + y' 0
=
⇔x0
=
hoặc x2.
=
0,25
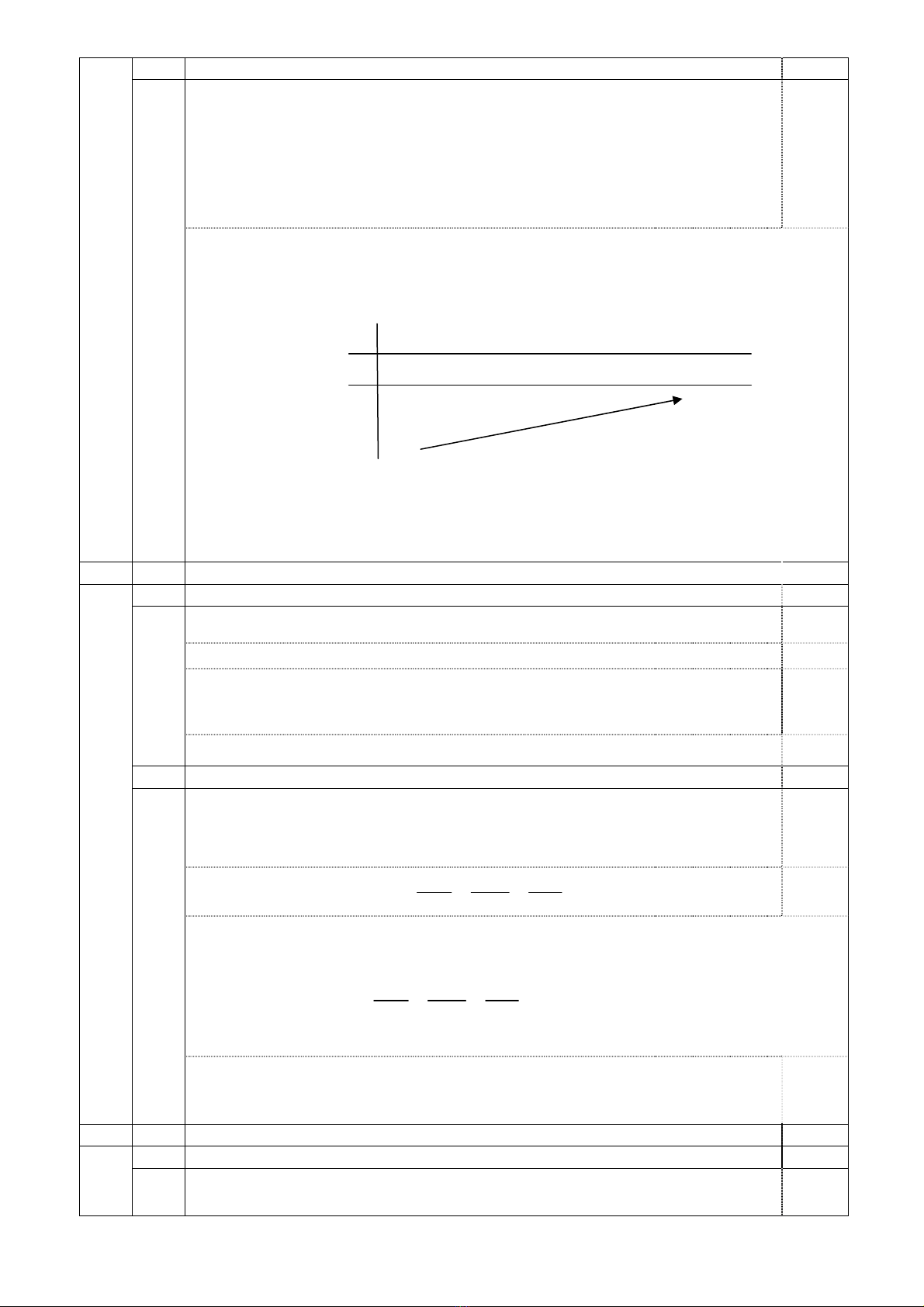
Bảng biến thiên:
yCĐ = y(2) = 0, yCT = y(0) = − 4.
0,50
• Đồ thị:
0,25
2 Tìm m để hàm số (1) có cực đại, cực tiểu … (1,00 điểm)
Ta có: 22
y' 3x 6x 3(m 1)=− + + − , y' = 0 ⇔ 22
x2xm10
−
−+= (2).
Hàm số (1) có cực trị ⇔ (2) có 2 nghiệm phân biệt ⇔ ∆' = m2 > 0 ⇔ m ≠ 0.
0,50
Gọi A, B là 2 điểm cực trị ⇒ A(1 − m; −2 − 2m3), B(1 + m; − 2 + 2m3).
O cách đều A và B ⇔ OA = OB ⇔ 8m3 = 2m ⇔ m = 1
2
±
(vì m ≠ 0).
0,50
II 2,00
1 Giải phương trình lượng giác (1,00 điểm)
Phương trình đã cho tương đương với:
(
)
2
sin 7x sin x 2sin 2x 1 0 cos 4x 2sin 3x 1 0.−+ −=⇔ −=
0,50
•
()
cos 4x 0 x k k .
84
ππ
=⇔= + ∈Z
• 12
sin 3x x k
2183
ππ
=⇔= + hoặc
()
52
xkk.
18 3
π
π
=+ ∈Z
0,50
x
−
∞ 02+ ∞
y
'
−
0+0 −
y
−
4 − ∞
+ ∞ 0
O
−
4
2
y
x
−
1
2/4
2 Chứng minh phương trình có hai nghiệm (1,00 điểm)
Điều kiện: x2.≥ Phương trình đã cho tương đương với
()
()
32
x2x 6x 32m 0−+−−= 32
x2
x6x32m0.
=
⎡
⇔⎢
+
−−=
⎣
Ta chứng minh phương trình:
(
)
32
x6x32m1+−= có một nghiệm trong
khoảng
()
2;
+
∞.
0,50
Xét hàm
(
)
32
fx x 6x 32=+ −với x2.> Ta có:
(
)
2
f' x 3x 12x 0, x 2.
=
+>∀>
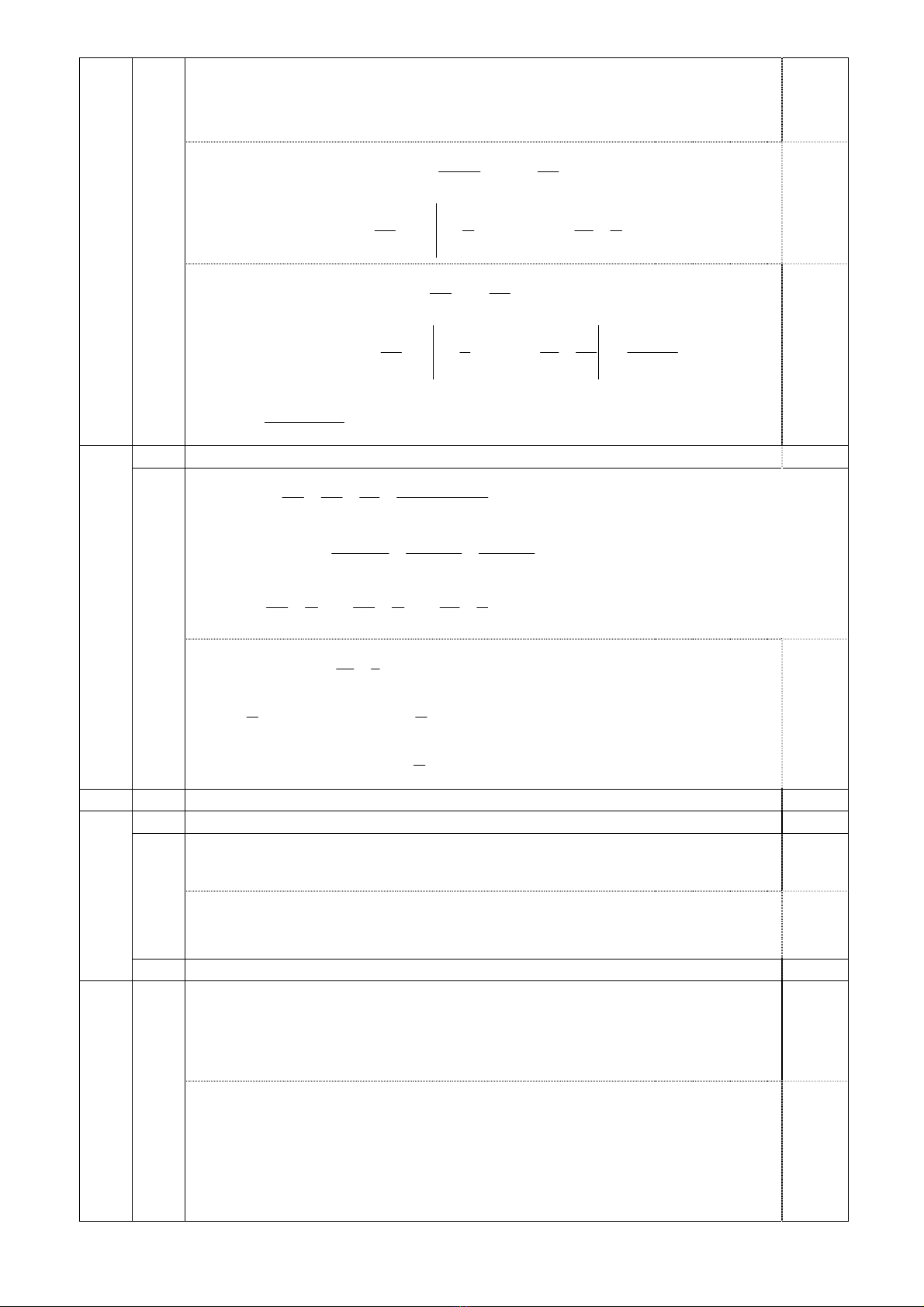
Bảng biến thiên:
Từ bảng biến thiên ta thấy với mọi m0>, phương trình (1) luôn có một
nghiệm trong khoảng
()
2;
+
∞.
Vậy với mọi m0> phương trình đã cho luôn có hai nghiệm thực phân biệt.
0,50
III 2,00
1 Viết phương trình mặt phẳng (Q) (1,00 điểm)
()( ) ( ) ( )
222
S:x 1 y 2 z 1 9−++ ++= có tâm
(
)
I1; 2; 1
−
− và bán kính R3.= 0,25
Mặt phẳng (Q) cắt (S) theo đường tròn có bán kính R = 3 nên (Q) chứa I. 0,25
(Q) có cặp vectơ chỉ phương là:
(
)
(
)
OI 1; 2; 1 , i 1;0;0=−− =
J
JG G
.
⇒ Vectơ pháp tuyến của (Q) là:
(
)
n0;1;2.=−
G
0,25
Phương trình của (Q) là:
(
)
(
)
(
)
0. x 0 1. y 0 2 z 0 0 y 2z 0.
−
−−+−=⇔−= 0,25
2 Tìm tọa độ điểm M thuộc mặt cầu sao cho khoảng cách lớn nhất (1,00 điểm)
Gọi d là đường thẳng đi qua I và vuông góc với (P). Đường thẳng d cắt (S) tại
hai điểm A, B . Nhận xét: nếu
(
)
(
)
(
)
(
)
dA;P dB;P≥ thì
()
(
)
dM;P lớn nhất
khi MA.≡
0,25
Phương trình đường thẳng d: x1 y2 z1
.
212
−
++
==
−
0,25
Tọa độ giao điểm của d và (S) là nghiệm của hệ
()( )()
222
x1 y2 z1 9
x1 y2 z1
.
212
⎧
−
++ ++ =
⎪
⎨−++
==
⎪
⎩−
Giải hệ ta tìm được hai giao điểm
(
)
(
)
A 1; 1; 3 , B 3; 3;1 .−−− −
0,25
Ta có:
()
()
(
)
()
dA;P 7 dB;P 1.=≥ =
Vậy khoảng cách từ M đến (P) lớn nhất khi
(
)
M1;1;3.
−
−−
0,25
IV 2,00
1 Tính thể tích vật thể tròn xoay (1, 00 điểm)
Phương trình hoành độ giao điểm của các đường yxlnx
=
và y0= là:
xlnx 0 x 1.
=
⇔= 0,25
f(x)
f '(x) +
0
x 2 + ∞
+ ∞
3/4
Thể tích khối tròn xoay tạo thành khi quay hình H quanh trục hoành là:
()
ee
2
2
11
V y dx x ln x dx.=π =π
∫∫
0,25
Đặt
3
22 2lnx x
u ln x,dv x dx du dx, v .
x3
==⇒= = Ta có:
()
e
eee
33
222 2
111
1
x2 e2
x ln x dx ln x x ln xdx x ln xdx.
33 33
=− =−
∫∫∫
0,25
Đặt
3
2dx x
ulnx,dvxdx du ,v .
x3
==⇒== Ta có:
ee
ee
3333
22
11
11
x1 ex2e1
x ln xdx ln x x dx .
33 399
+
=−=−=
∫∫
Vậy
(
)
3
5e 2
V27
π−
= (đvtt).
0,25
2 Tìm giá trị nhỏ nhất của P (1,00 điểm)
Ta có:
222222
xyzxyz
P.
222 xyz
++
=+++
Do
22 22 22
222
xy yzzx
xyz xyyzzx
222
+++
++= + + ≥++
nên
222
x1 y1 z1
P.
2x 2y 2z
⎛⎞⎛⎞⎛⎞
≥+++++
⎜⎟⎜⎟⎜⎟
⎜⎟⎜⎟⎜⎟
⎝⎠⎝⎠⎝⎠
0,50
Xét hàm số
()
2
t1
ft 2t
=+ với t0.> Lập bảng biến thiên của f(t) ta suy ra
()
3
ft , t 0.
2
≥∀> Suy ra: 9
P.
2
≥ Dấu bằng xảy ra
⇔
xyz1.
=
==
Vậy giá trị nhỏ nhất của P là 9.
2
0,50
V.a 2,00
1 Tìm hệ số trong khai triển… (1,00 điểm)
Ta có:
() ( )
nn
n0 n11 n22 n n
nn n n
3 C 3 C 3 C ... 1 C 3 1 2
−−
−+ −+−=−=.
Từ giả thiết suy ra n11=.
0,50
Hệ số của số hạng chứa 10
x trong khai triển Niutơn của
()
11
2x+ là:
10 1
11
C .2 22.=
0,50
2 Xác định tọa độ điểm B, C sao cho …(1,00 điểm)
Vì 12
Bd,Cd∈∈ nên
()
(
)
Bb;2 b,Cc;8 c.
−
− Từ giả thiết ta có hệ:
(
)
(
)
()()
22
22
b1c 4 2
bc 4b c 2 0
AB.AC 0
AB AC b2bc8c18
b
1c43.
−−=
⎧
−−+=
⎧
⎧=
⎪⎪ ⎪
⇔⇔
⎨⎨ ⎨
=−=−+
⎪⎪
−
−− =
⎩⎩⎪
⎩
JJJG JJJG
0,50
Đặt x b 1, y c 4=− =− ta có hệ 22
xy 2
xy3.
=
⎧
⎪
⎨
−
=
⎪
⎩
Giải hệ trên ta được x 2, y 1=− =− hoặc x 2, y 1
=
=.
Suy ra:
()()
B1;3,C3;5− hoặc
(
)
(
)
B3; 1,C5;3−.
0,50
4/4
V.b 2,00
1 Giải phương trình mũ (1,00 điểm)
Đặt
()
()
x
21 tt 0,−= > ta có phương trình
1
t220t21,t21.
t
+− =⇔=−=+
0,50
Với t21=−
ta có x1.=
Với t21=+ ta có x1.=− 0,50
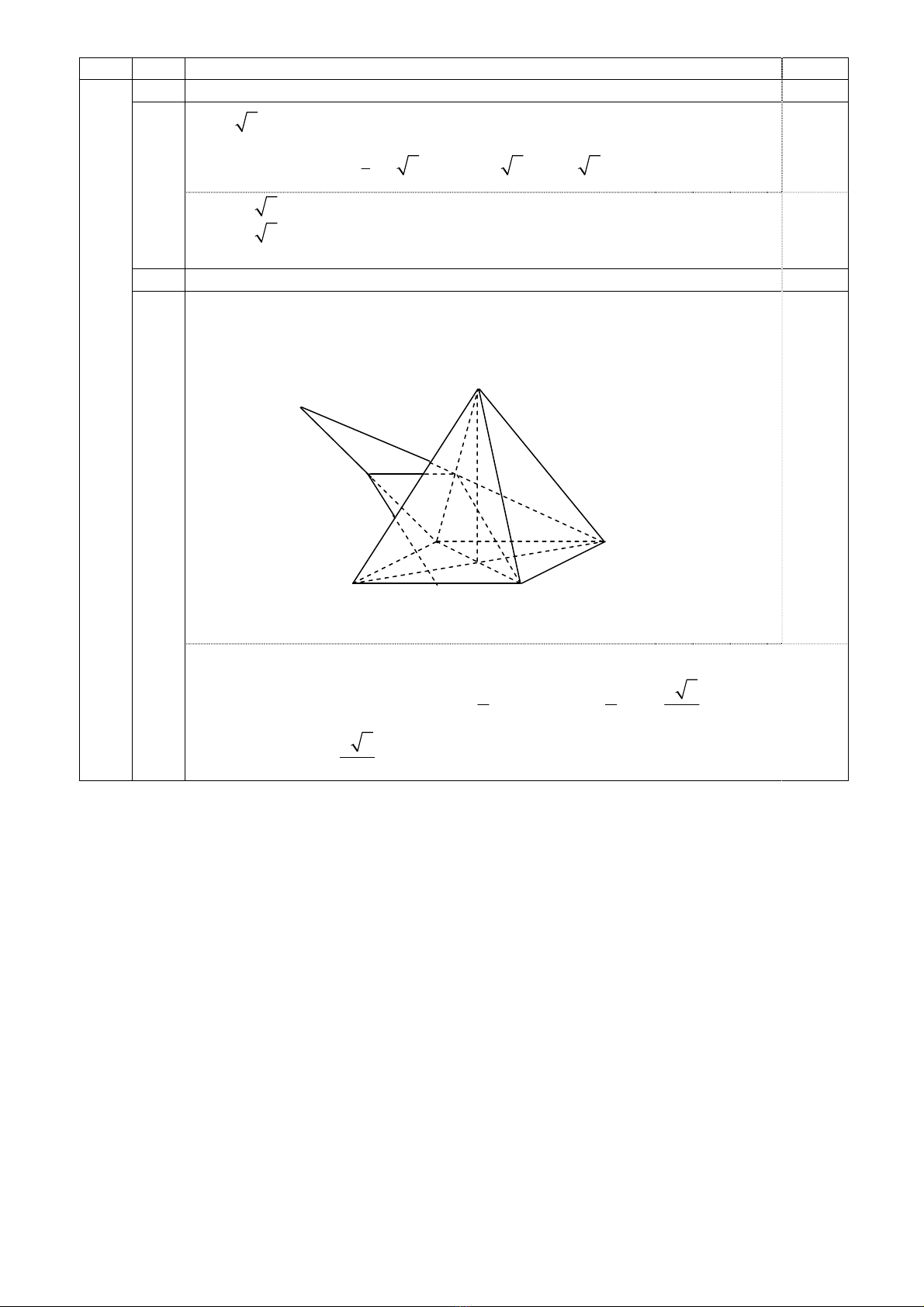
2 (1,00 điểm)
Gọi P là trung điểm của SA. Ta có MNCP là hình bình hành nên MN song
song với mặt phẳng (SAC). Mặt khác,
(
)
BD SAC⊥ nên BD MN.⊥
0,50
Vì
()
MN || SAC nên
()() ()
()
11a2
d MN;AC d N;(SAC d B; SAC BD .
244
== ==
Vậy
()
a2
dMN;AC .
4
=
0,50
NÕu thÝ sinh lµm bµi kh«ng theo c¸ch nªu trong ®¸p ¸n mµ vÉn ®óng th× ®−îc ®ñ ®iÓm tõng
phÇn nh− ®¸p ¸n quy ®Þnh.
----------------Hết----------------
N
E
C
B
M
P
D
A
S
















