S GIÁO D C VÀ ĐÀO T O Đ K L KỞ Ụ Ạ Ắ Ắ
TR NG THPT NGUY N HUƯỜ Ễ Ệ Đ THI TH Đ I H C Ề Ử Ạ Ọ
MÔN TOÁN NĂM 2012 - 2013
Th i gian làm bài: 180 phútờ.
I. PH N CHUNG CHO T T C THÍ SINH (7 đi m)Ầ Ấ Ả ể
Câu I: (2.0 đi m) ểCho hàm s ố
y x x
3 2
3 1= − +
có đ th (C).ồ ị
1) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
2) Tìm hai đi m A, B thu c đ th (C) sao cho ti p tuy n c a (C) t i A, B song song v i nhau và AB=ể ộ ồ ị ế ế ủ ạ ớ
4 2
.
Câu II : (3.0 đi m)ể
1) Cho h ph ng trình: ệ ươ
3 3
( )
2
x y m x y
x y
+ = +
− =
. Tìm t t c các giá tr c a tham s m đ h ph ng trình cóấ ả ị ủ ố ể ệ ươ
ba nghi m phân bi t (xệ ệ 1; y1), (x2; y2) và (x3; y3) sao cho x1, x2, x3 l p thành m t c p s c ng.ậ ộ ấ ố ộ
2) Gi i ph ng trình: cotx – 1 =ả ươ
2
os2x 1
sin sin 2
1 + tanx 2
cx x+ −
.3) Tính
22
3
1
1x
I dx
x x
−
=+
Câu III : (2.0 đi m)ể
1) Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O, c nh a, góc BAD = ạ
0
60
, SO
⊥
(ABCD) và
SO = a. Tính kho ng cách gi a hai đ ng th ng AD và SB theo a.ả ữ ườ ẳ
2) Cho x, y, z là các s th c d ng th a mãn: ố ự ươ ỏ x2 + y2 + z2 ≤ 3. Tìm giá tr nh nh t c a bi u th c:ị ỏ ấ ủ ể ứ
1 1 1
1 1 1
Pxy yz zx
= + +
+ + +
II. PH N RẦIÊNG (3 đi m). THÍ SINH CH N M T TRONG HAI PH N SAUể Ọ Ộ Ầ
1. Theo ch ng trình C b nươ ơ ả
Câu IVa: (2.0 đi m)ể
1) Trong m t ph ng t a đ ặ ẳ ọ ộ
cho tam giác ABC, các đ ng th ng ch a đ ng cao và đ ng trungườ ẳ ứ ườ ườ
tuy n k t đ nh ế ẻ ừ ỉ A có ph ng trình l n l t là: ươ ầ ượ
0132 =−− yx
và
.09613 =−− yx
Tìm t a đ các đ nh ọ ộ ỉ B
và C bi t tâm đ ng tròn ngo i ti p tam giác ABC là ế ườ ạ ế
).1;5(−I
2) Trong kh«ng gian víi hÖ täa ®é Oxyz cho ®iÓm A(10; 2; -1) vµ ®êng th¼ng d:
1 1
2 1 3
x y z− −
= =
.
LËp ph¬ng tr×nh mÆt ph¼ng (P) ®i qua A, song song víi d vµ kho¶ng c¸ch tõ d tíi (P) lµ lín nhÊt.
Câu Va: (1.0 đi m). Gi i ph ng trình:ể ả ươ
10)2)(3)((
2
=++−
zzzz
,
∈z
ﾣ
.
2. Theo ch ng trình Nâng caoươ
Câu IVb: (2.0 đi m)ể
1) Trong m t ph ng to đ Oxy cho tam giác ABC, có đi m A(2; 3), tr ng tâm G(2; 0). Hai đ nh B và Cặ ẳ ạ ộ ể ọ ỉ
l n l t n m trên hai đ ng th ng dầ ượ ằ ườ ẳ 1: x + y + 5 = 0 và d2: x + 2y – 7 = 0. Vi t ph ng trình đ ng trònế ươ ườ
có tâm C và ti p xúc v i đ ng th ng BG.ế ớ ườ ẳ
2) Trong không gian to đ cho đ ng th ng d: ạ ộ ườ ẳ
3 2 1
2 1 1
x y z− + +
= = −
và m t ph ng (P): x + y + z + 2 = 0.ặ ẳ
G i M là giao đi m c a d và (P). Vi t ph ng trình đ ng th ng ọ ể ủ ế ươ ườ ẳ
∆
n m trong m t ph ng (P), vuông gócằ ặ ẳ
v i d đ ng th i tho mãn kho ng cách t M t i ớ ồ ờ ả ả ừ ớ
∆
b ng ằ
42
.
Câu Vb: (1.0 đi m) Gi i h ph ng trình ể ả ệ ươ
( )
1 4
4
2 2
1
log log 1 ( , )
25
y x yx y
x y
− − =
+ =
ﾣ
------------------------- h t ----------------------------ế
(Thí sinh không s d ng tài li u, giám th không gi i thích gì thêm!ử ụ ệ ị ả )
H và tên thí sinh: ...................................ọ.........................., s báo danh: ....................ố
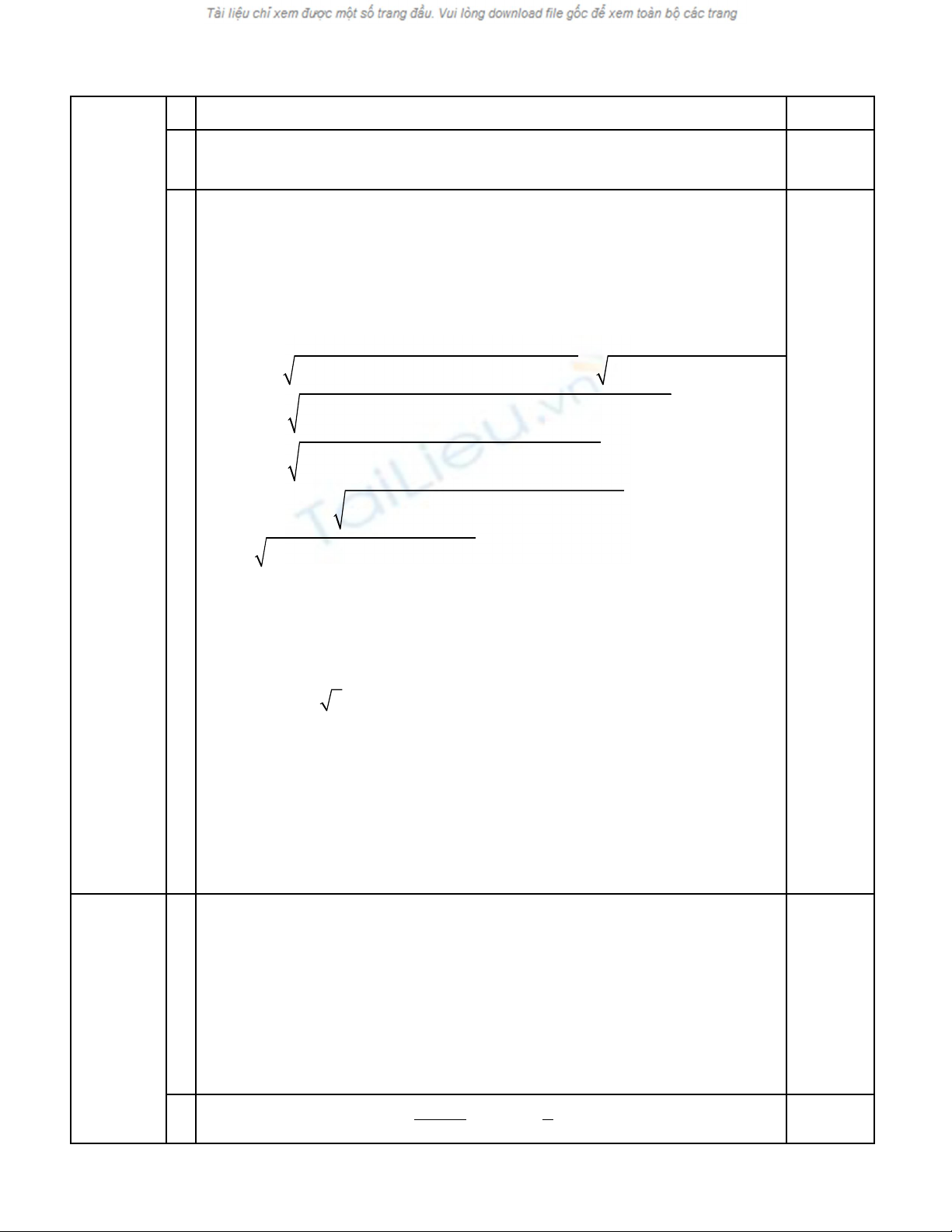
ĐÁP ÁN VÀ THANG ĐI MỂ
Câu I
Cho hàm s ố
y x x
3 2
3 1= − +
có đ th (C)ồ ị
1
- T p xác đ nhậ ị
- S bi n thiênự ế
- Đ ồthị
0.25
0.5
0.25
2
Gi s ả ử
A a a a B b b b
3 2 3 2
( ; 3 1), ( ; 3 1)− + − +
thu c (C), v i ộ ớ
a b
.
Vì ti p tuy n c a (C) t i A và B song song v i nhau nên: ế ế ủ ạ ớ
y a y b( ) ( )
=
⇔
a a b b a b a b a b a b
2 2 2 2
3 6 3 6 2( ) 0 ( )( 2) 0− = − − − − = − + − =� �
⇔
a b b a2 0 2
+ − = = −�
. Vì
a b
nên
a a a2 1−� ۹
Tacó:
AB b a b b a a b a b a b a
2 3 2 3 2 2 2 3 3 2 2 2
( ) ( 3 1 3 1) ( ) ( 3( ))= − + − + − + − = − + − − −
b a b a ab b a b a b a
2
2 3
( ) ( ) 3 ( ) 3( )( )
� �
= − + − + − − − +
� �
b a b a b a ab
2
2 2 2
( ) ( ) ( ) 3 3.2
� �
= − + − − + −
� �
b a b a b a ab
2
2 2 2
( ) ( ) ( ) 6
� �
= − + − + − −
� �
b a b a ab
2 2 2
( ) ( ) ( 2 )= − + − − −
2
AB b a ab a a a
2 2 2 2 2
( ) 1 ( 2 ) (2 2 ) 1 ( 2 2)
� � � �
= − + − − = − + − −
� � � �
a a a a a
2
2 2 2 4 2
4( 1) 1 ( 1) 3 4( 1) ( 1) 6( 1) 10
� �
� � � �
= − + − − = − − − − +
� �
� � � �
� �
a a a
6 4 2
4( 1) 24( 1) 40( 1)= − − − + −
Mà
AB 4 2=
nên
a a a
6 4 2
4( 1) 24( 1) 40( 1) 32− − − + − =
a a a
6 4 2
( 1) 6( 1) 10( 1) 8 0− − − + − − =�
(*)
Đ t ặ
t a t
2
( 1) , 0= − >
. Khi đó (*) tr thành:ở
t t t t t t t
3 2 2
6 10 8 0 ( 4)( 2 2) 0 4− + − = − − + = =� �
⇒
a b
aa b
23 1
( 1) 4 1 3
= = −�
− = = − =�
V y 2 đi m tho mãn YCBT là: ậ ể ả
A B(3;1), ( 1; 3)− −
.
0.25
0.25
0.25
0.25
Câu II
1
Cho h ph ng trình: ệ ươ
3 3
( )(1)
2(2)
x y m x y
x y
+ = +
− =
+ T (2), ta có y = x ừ− 2 thay vào (1) ta có :
(2x - 2)[x2 - 2x + 4 - m] = 0 ⇔
2
1
2 4 0(*)
x
x x m
=
− + − =
+ Nh n xétậ : (*) có 2 nghi m xệ1, x2 phân bi t thì : xệ1 < 1 < x2 và x1 + x2 = 2. (th aỏ
mãn 3 nghi m l p thành c p s c ng v i m i m đ pt có 2 nghi m phân bi tệ ậ ấ ố ộ ớ ọ ể ệ ệ )
+ YCBT ⇔ pt (*) có 2 nghi m phân bi t ệ ệ ⇔ ∆' = 1 - 4 + m > 0 ⇔ m > 3
0.25x4
2Gi i ph ng trình: cotx – 1 =ả ươ
2
os2x 1
sin sin 2
1+tanx 2
cx x+ −
.0.25x4