S GIÁO D C VÀ ĐÀO T O Đ K L KỞ Ụ Ạ Ắ Ắ
TR NG THPT NGUY N HUƯỜ Ễ Ệ Đ THI TH Đ I H C Ề Ử Ạ Ọ
MÔN TOÁN NĂM 2012 - 2013
Th i gian làm bài: 180 phútờ.
I. PH N CHUNG CHO T T C CÁC THÍ SINH Ầ Ấ Ả (7 đi m)ể
Câu I (2 đi m)ể
Cho hàm s ố
y
=
2)1(2
24
−+−− mxmx
(1).
1. Kh o sát s bi n thiên và v đ th (C) c a hàm s (1) khi ả ự ế ẽ ồ ị ủ ố
2
=
m
.
2. Tìm
m
đ hàm s (1) đ ng bi n trên kho ng (3,ể ố ồ ế ả
5)
.
Câu II (2 đi m)ể
1. Gi i ph ng trình: ả ươ
3sin cos 2 cos 2 sin 2 0x x x x− + − − =
2. Gi i ph ng trình: ả ươ
( )
2 2
x 41x 4x x 18 3 4 x 2x 44x 18+ − + + + +
Câu III (2 đi m)ể. Tính tích phân: I =
2
0
4 .sinx cos 2
2sin 1
x x x dx
x
π
− +
+
Câu IV (1 đi m)ể Cho hình lăng tr đ ng ụ ứ
có tam giác
ABC
vuông t i ạ
C
.
M
là trung
đi m c a ể ủ
' '
A C
. Bi t ế
AC
=
a
,
BC
=
3a
;
( )
'
ABC
h p v i ợ ớ
( )
ABC
góc
0
60
. Tính th tích kh iể ố
lăng tr ụ
' ' '
.ABC A B C
V
và Kho ng cách ả
( )
'
AM,BC
d
theo
a
.
Câu V (1 đi m)ể Cho ba s ố
[ ]
x, y,z 1;3
tìm giá tr nh nh t c a: ị ỏ ấ ủ
36x 2y z
Pyz xz xy
= + +
II. PH N RIÊNG Ầ(3 đi m)ể
Thí sinh ch đ c làm m t trong hai ph n ỉ ượ ộ ầ (ph n A ho c B)ầ ặ
A. Theo ch ng trình Chu nươ ẩ
Câu VI.a (2 đi m)ể
1. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ Oxy, cho tam giác ABC có đ nh ỉ
( )
B 2;0
;
( )
C 3;5−
. G Là tr ngọ
tâm thu c đ ng th ng d có ph ng trình là ộ ườ ẳ ươ
2x y 1 0+ − =
và di n tích tam giácệ ABC b ng ằ
5
2
.
Hãy xác đ nh t a đ đi m Aị ọ ộ ể ?
2. Trong m t ph ng v i h t a đ Oxyz, cho đi m H(3ặ ẳ ớ ệ ọ ộ ể ;-2 ;1) vi t ph ng trình m t ph ng quaế ươ ặ ẳ
H c t các tr c t a đ t i A,B,C sao cho H là tr c tâm tam giác ABCắ ụ ọ ộ ạ ự
Câu VII.b (1 đi m)ể . Gi i ph ng trình: ả ươ
( )
2
1 2
2
log 4 log 3 3 0x x x x+ − − + =
B. Theo ch ng trình Nâng cao ươ
Câu VI.b (2 đi m)ể
1. Trong m t ph ng v i h t a đ ặ ẳ ớ ệ ọ ộ
Oxy
, cho elip
( )
2 2
x y
E : 1
25 9
+ =
và
9 9
I ;
2 10
� �
� �
� �
. Xác đ nh haiị
đi m A và B thu c elip sao cho I là trung đi m c a ABể ộ ể ủ
2. Trong m t ph ng v i h t a ặ ẳ ớ ệ ọ đ ộOxyz , cho m t c u (ặ ầ
S
) có ph ng trìnhươ
2 2 2 2 4 6 11 0x y z x y z+ + − + + − =
và đi m ể
( )
A 1; 2; 2− − −
m t ph ng ặ ẳ
( )
P
là m t ph ng qua ặ ẳ
A
và
c t m t c u ắ ặ ầ
( )
S
theo thi t di n là đ ng tròn có bán kính nh nh t. Hãy vi t ph ng trình m tế ệ ườ ỏ ấ ế ươ ặ
ph ng ẳ
( )
P
và tính bán kính c a đ ng tròn giao tuy n đó. ủ ườ ế
Câu VI.b (1 đi m)ể E là t p các s t nhiên g m 5 ch s khác nhau đ c l p t các ch sậ ố ự ồ ữ ố ượ ậ ừ ữ ố :
0,1,2,3,4,5,6,7. l y ng u nhiên m t s trong E tính xác su t đ l y đ c s chia h t cho 5.ấ ẫ ộ ố ấ ể ấ ượ ố ế
----------------------------- H t ế-----------------------------
Thí sinh không đ c s d ng tài li u. Cán b coi thi không gi i thích gì thêmượ ử ụ ệ ộ ả .
H và tên thí sinhọ .........................................................s báo danh........................ố
H NG D N ƯỚ Ẫ
Câu Đáp án Đi mể
I
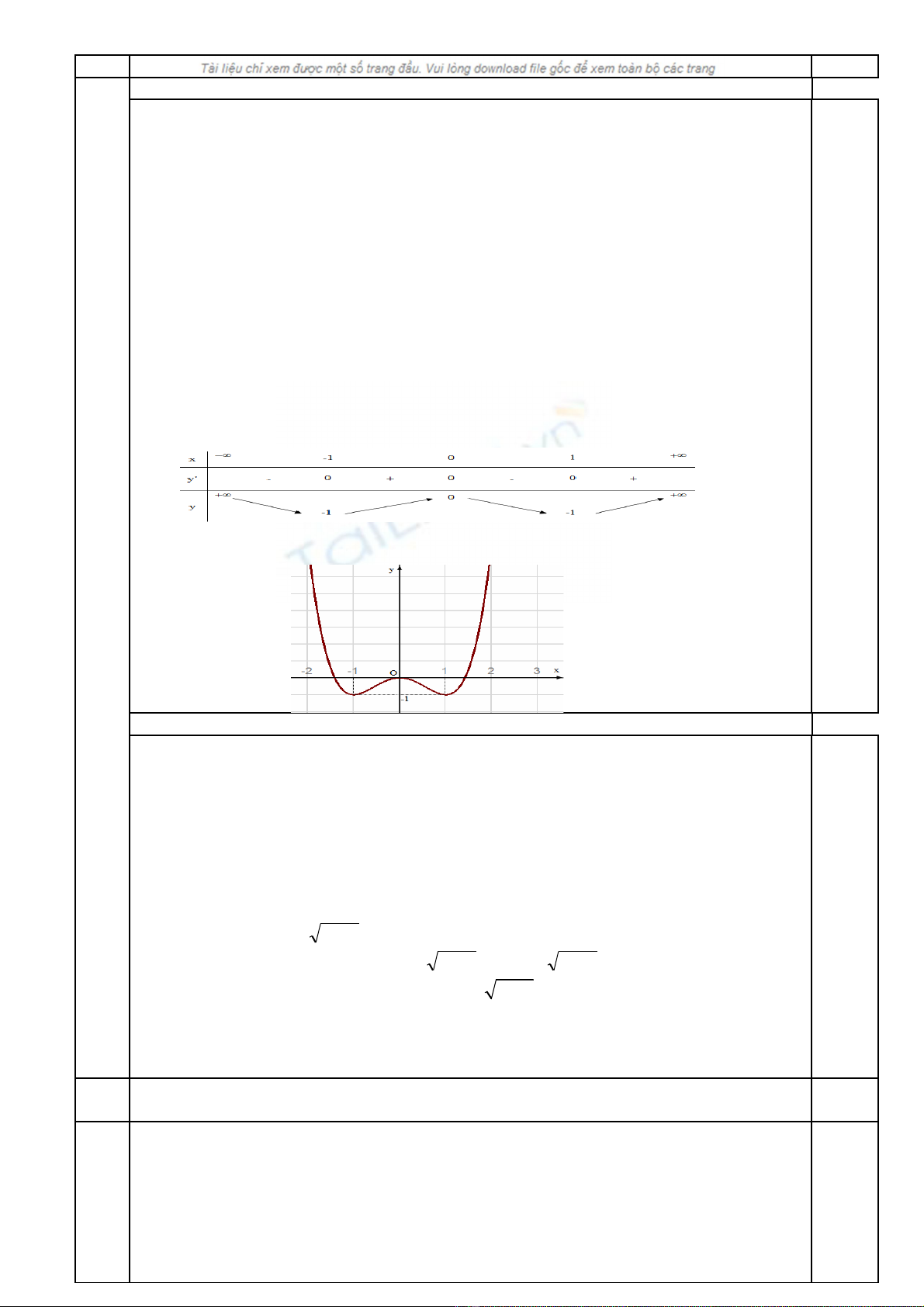
(2đ)
1. (1 đi m)ể
V i m = 2, ớ
24 2xxy −=
1. TXĐ: D =
R
2. S bi n thiên:ự ế
a) Chi u bi n thiên:ề ế
xxy 44' 3−=
;
⇔= 0'y
1,0044 3±==⇔=− xxxx
Hàm s đ ng bi n trên các kho ng (-1; 0) và (1; ố ồ ế ả
∞+
)
Hàm s ngh ch bi n trên các kho ng (-ố ị ế ả
∞
; -1) và (0; 1)
-----------------------------------------------------------------------------------------------------
b) C c tr :ự ị
Hàm s đ t c c đ i t i x = 0; yố ạ ự ạ ạ cđ = y(0) = 0
Hàm s đ t c c ti u t i x = ố ạ ự ể ạ
±
1; yct = y(
±
1) = -1
----------------------------------------------------------------------------------------------------
c) Gi i h n t i vô c c:ớ ạ ạ ự
=−
± ∞→ )2( 24 xxLim
x
+
∞
d) B ng bi n thiênả ế B ng bi n thiênả ế
-----------------------------------------------------------------------------------------------------
3) Đ th :ồ ị
0,25 đ
0,25đ
0,25 đ
0,25 đ
2) 1 đi mể
y' =
xmx )1(44 3−−
y' = 0
⇔
xmx )1(44 3−−
= 0
⇔
[ ]
0)1(
2=−− mxx
----------------------------------------------------------------------------------------------------
TH1: N u m- 1 ế
≤
0
⇔
m
≤
1
Hàm s đ ng bi n trên kho ng (0; +ố ồ ế ả
∞
).
V y m ậ
≤
1 tho mãn ycbtả
---------------------------------------------------------------------------------------------------
TH 2: m - 1 > 0
⇔
m> 1
y' = 0
⇔
x = 0, x =
1−± m
Hàm s đ ng bi n trên các kho ng (-ố ồ ế ả
1−m
; 0 ) và (
1−m
; +
∞
)
Đ hàm s đ ng bi n trên kho ng (3; 5 ) thì ể ố ồ ế ả
1 3m−
⇔
m
≤
10
-----------------------------------------------------------------------------------------------------
V y hàm s đ ng bi n trên kho ng (3; 5) ậ ố ồ ế ả
⇔
m
∈
(
]
;10−
0,25 đ
0,25 đ
0,25 đ
0,25 đ
II
(2 đ)
1. (1 đi m)ể
2
sin x cos x 1 2sin x 2sin x 2sin x cos x 0− + + + − =
⇔
(1+2sinx)(sinx - cosx +1) = 0
-------------------------------------------------------------------------------------------------------
0,25 đ
0,25 đ
2
sinx cos x 1 sin(x )
4 2
1
sinx 1
sinx
22
Π −
− = −
− =
� �
−
=−
=
⇔
72
6
2
6
32
2
2
x k
x k
x k
x k
ππ
ππ
ππ
π
= +
−
= +
= +
=
kﾢ
0, 5 đ
2. (1 đi m)ể
I =
2 2 2
0 0 0
2 2
2
2
0
2 (1 2sin ) os os
2
1 2sin 1 2sin
1(1 2sin ) 1 2ln 3
2ln 1 2sin
2 2
1 2sin 4 2 4
0 0
x x c x c x
I dx xdx dx
x x
d x
x x
x
π π π
π
π π
π π
+ −
= = −
+ +
+−
= − = − + =
+
� � �
0,25 đ
0, 5 đ
0,25 đ
III
(2 đ)
1. (1 đi m)ể
Đk:
x 0
bpt
2 2 2
2x 44x 18 x 3x 4x x (3 4 x) 2x 44x 18+ + − − − + + +
Đ t : ặ
2
t 2x 44x 18= + +
(t>0)
Đc bpt:
2 2
t x x(3 4 x ) (3 4 x)t 0
(t x)(t x 3 4 x) 0 t x 3 4 x 0
− − + − +
+ − − − − − −� � � �
vì t+x>0 v i m i xớ ọ
0
--------------------------------------------------------------------------------------------------------
Ta có bpt
2
2x 44x 18 x 3 4 x+ + + −� �
2
2 2
2
2(x 3) 32x (x 3) 4 x
2(x 3) 32x ((x 3) 4 x)
x 1
(x 3 4 x ) 0 x 3 4 x 0 x 9
+ + + +� �
+ + + +� �
=
+ − + − =� � � � =
0,25 đ
0,25 đ
0, 5 đ
IV
(1 đ) T gi thi t có ừ ả ế
' ' '
.ABC A B C
V
=
ABC
S .CC';
∆
ABC
S
∆
=
2
1 a 3
CA.CB
2 2
=
(ABC') (ABC) AB=I
, K ẻ
ﾢ
ﾢ
ﾢ
0
CH AB H AB (CC'H)
60 ((ABC'),(ABC)) (CH,HC') CHC'
⊥ = ⊥�
= = =�
Xét tam giác vuông ABC có CH là chi u cao nênề
2 2 2 2 2 2
CH CA CB 3a a 3a
1 1 1 1 1 4 a 3
CH 2
= + = + = =�
, Xét tam giác vuông CHC’ có
' ' '
2 3
0
ABC.A BC
3a a 3 3a a 3 3
CC ' HC tan 60 V .
2 2 2 4
= = = =�
----------------------------------------------------------------------------------------------------------------------------------------------------
b.N là trung đi m c a AC thì AM//C’N nên AM//(BC’N)ể ủ
( ) ( ) ( )
' ' '
AM,BC AM,(BC N) A,(BC N)
d d d= =
. N là trung đi m c a ACể ủ
Nên
( ) ( )
' '
A,(BC N) C,(BC N)
d d=
, k CK vuông góc v i BC’ẻ ớ
0,25 đ
0,25 đ