Hiendvtiger.violet.vn KỲ THI T T NGHI P TRUNG H C PH THÔNGỐ Ệ Ọ Ổ
Đ THI TH T T NGHI PỀ Ử Ố Ệ Môn thi: TOÁN − Giáo d c trung h c ph thôngụ ọ ổ
CODE 13 Th i gian làm bài: 150 phút, không k th i gian giao đờ ể ờ ề
------------------------------ ---------------------------------------------------
I. PH N CHUNG DÀNH CHO T T C CÁC THÍ SINH (7,0 đi m)Ầ Ấ Ả ể
Câu I (3,0 đi m): ểCho hàm s : ố
2 2
( 2) 1y x= - -
1) Kh o sát s bi n thiên và v đ th ả ự ế ẽ ồ ị
( )C
c a hàm s .ủ ố
2) D a vào đ th (ự ồ ị C) bi n lu n s nghi m ph ng trình: ệ ậ ố ệ ươ
4 2
4x x m- =
.
Câu II (3,0 đi m):ể
1) Gi i ph ng trình: ả ươ
22
log ( 5) log 2 3x x- + + =
2) Tính tích phân:
3
ln 2
0
1
x
x
e
I dx
e
+
=
￲
3) Tìm giá tr l n nh t, giá tr nh nh t c a hàm s : ị ớ ấ ị ỏ ấ ủ ố
3 2
1
x
yx
-
=
+
trên đo nạ
[1; 4]
Câu III (1,0 đi m):ể
Cho hình lăng tr ụ
.A BC A B C
￲ ￲ ￲
có đáy ABC là tam giác đ u c nh b ng ề ạ ằ a. Hình chi u vuông góc c a ế ủ
xu ng m t ph ng (ố ặ ẳ ABC) là trung đi m c a ể ủ AB. M t bên ặ
( )A A C C
￲ ￲
t o v i đáy m t góc b ng ạ ớ ộ ằ
45
o
. Tính
th tích c a kh i lăng tr này.ể ủ ố ụ
II. PH N RIÊNG (3,0 đi m) Ầ ể Thí sinh ch đ c ch n m t trong hai ph n d i đâyỉ ượ ọ ộ ầ ướ
1. Theo ch ng trình chu nươ ẩ
Câu IVa (2,0 đi m): ểTrong không gian Oxyz, cho hai đi m ể
(0;1; 4), (1; 0; 5)A B- -
và đ ng th ngườ ẳ
1 4 1
:1 4 2
x y z- - -
= =D- -
1) Vi t ph ng trình đ ng th ng ế ươ ườ ẳ AB và ch ng minh r ng ứ ằ AB và
D
chéo nhau.
2) Vi t ph ng trình m t ph ng (ế ươ ặ ẳ P) ch a hai đi m ứ ể A,B đ ng th i song song v i đ ng th ng ồ ờ ớ ườ ẳ
D
. Tính
kho ng cách gi a đ ng th ng ả ữ ườ ẳ
D
và m t ph ng (ặ ẳ P).
Câu Va (1,0 đi m):ể Tính di n tích hình ph ng gi i h n b i: ệ ẳ ớ ạ ở
2
12 36y x x= - +
và
2
6y x x= -
2. Theo ch ng trình nâng caoươ
Câu IVb (2,0 đi m): ểTrong không gian Oxyz, cho hai đ ng th ng:ườ ẳ
1 2
13 1
: 1 : 1 2 1
2
x t x y z
y t
z
￲
￲= +
￲
￲- -
￲= - - = =D D
￲
￲-
￲=
￲
￲
￲
1) Ch ng minh ứ
1
D
và
2
D
chéo nhau. Vi t ph ng trình mp(ế ươ P) ch a ứ
1
D
và song song
2
D
.
2) Tìm đi m ểA trên
1
D
và đi m ểB trên
2
D
sao cho đ dài đo n ộ ạ AB ng n nh t.ắ ấ
Câu Vb (1,0 đi m):ể Trên t p s ph c, tìm ậ ố ứ B đ ph ng trình b c hai ể ươ ậ
2
0z Bz i+ + =
có t ng bình ph ng haiổ ươ
nghi m b ng ệ ằ
4i-
---------- H t ----------ế
Thí sinh không đ c s d ng tài li u. Giám th coi thi không gi i thích gì thêm.ượ ử ụ ệ ị ả
H và tên thí sinh: ........................................ọ S báo danh: ...............................................ố
Ch ký c a giám th 1: ..................................ữ ủ ị Ch ký c a giám th 2: .................................ữ ủ ị
x
y
y
=
m
+ 3
-2
-1
3
2
-1
O
1
BÀI GI I CHI TI TẢ Ế .
Câu I:
Hàm s : ố
2 2 4 2 4 2
( 2) 1 4 4 1 4 3y x x x x x= - - = - + - = - +
￲ T p xác đ nh: ậ ị
D=ﾡ
￲ Đ o hàm: ạ
3
4 8y x x
￲= -
￲ Cho
3 2
0
0 4 8 0 4 ( 2) 2
x
y x x x x x
￲=
￲
￲= - = -� � � ￲= ￲
￲
￲
￲ Gi i h n: ớ ạ
; lim lim
x x
y y
￲ - ￲ ￲ +￲
= +￲ = +￲
￲ B ng bi n thiênả ế
x–￲
2-
0
2
+￲
y￲
–0+0–0+
y
+￲
3
+￲
–1 –1
￲ Hàm s ĐB trên các kho ng ố ả
( 2; 0),( 2; )- +￲
, NB trên các kho ng ả
( ; 2),(0; 2)- ￲ -
Hàm s đ t c c đ i ố ạ ự ạ
CÑ
3y=
t i ạ
CÑ
0x=
.
Hàm s đ t c c ti u ố ạ ự ể
CT
1y= -
t i ạ
CT
2x= ￲
.
￲ Giao đi m v i tr c hoành:ể ớ ụ
Cho
2
4 2
2
1
1
0 4 3 0 3
3
x
x
y x x x
x
￲￲= ￲
=
￲￲
= - + =� ��
￲￲= ￲
=
￲￲
￲
￲
Giao đi m v i tr c tung: cho ể ớ ụ
0 3x y= =�
￲ B ng giá tr : ả ị x –2 –1 0 1 2
y3–13–13
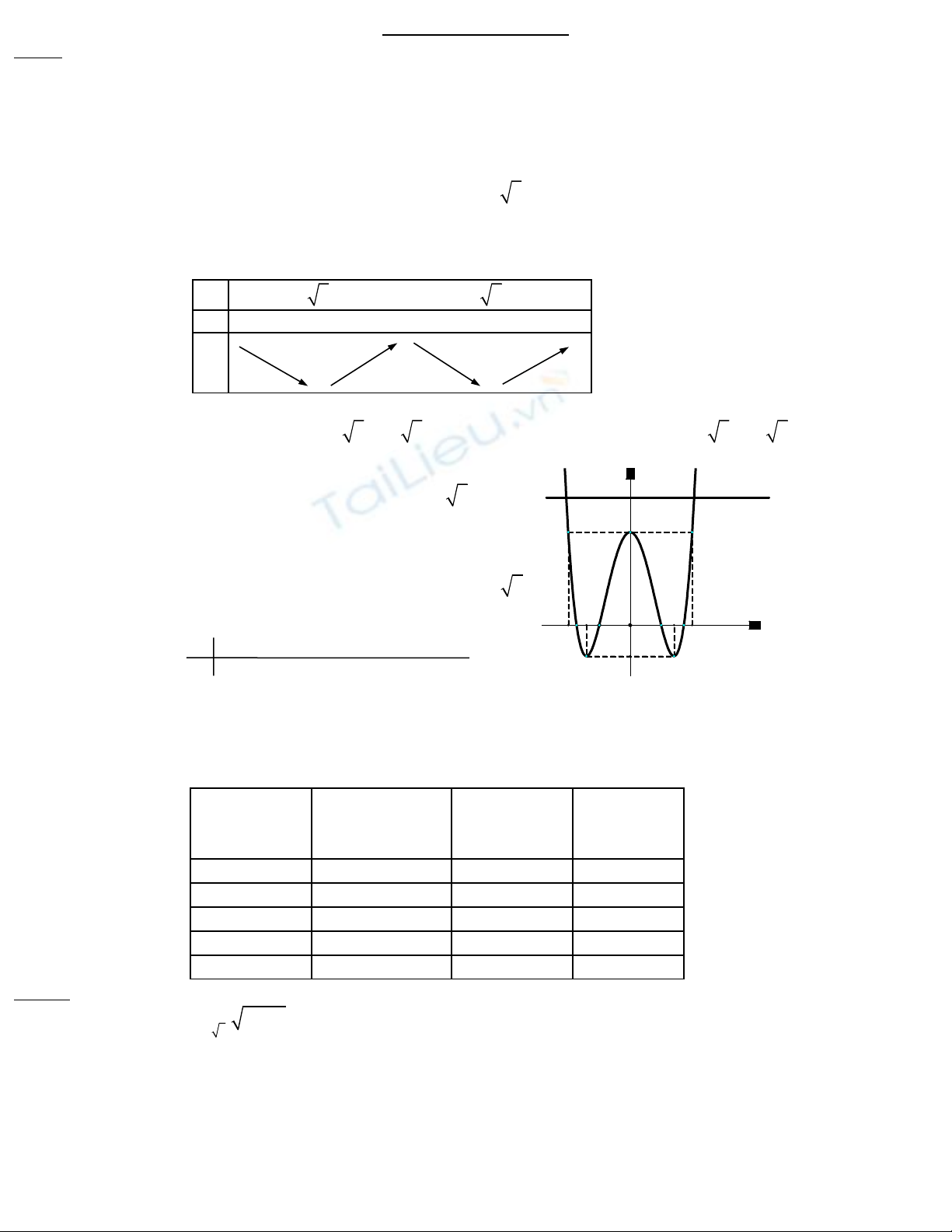
￲ Đ th hàm s : nh hình v bên đâyồ ị ố ư ẽ
￲
4 2 4 2
4 4 3 3x x m x x m- = - + = +�
(*)
￲ S nghi m c a ph ng trình ố ệ ủ ươ (*) b ng s giao đi m c a ằ ố ể ủ (C) và d: y = m + 3
￲ Ta có b ng k t qu nh sau:ả ế ả ư
m m + 3
S giaoố
đi mể
c a (ủC) và d
S nghi mố ệ
c a pt(*)ủ
m > 0 m + 3 > 3 2 2
m = 0 m + 3 = 3 3 3
–4 < m < 0 –1< m + 3 < 3 4 4
m = –4 m + 3 = –1 2 2
m < –4 m + 3 < –1 0 0
Câu II:
22
log ( 5) log 2 3x x- + + =
(*)
￲ Đi u ki n: ề ệ
5 0 5 5
2 0 2
x x x
x x
� �
� �
- > >
� � >� �
� �
� �
+ > > -
� �
� �
￲ Khi đó,
2 2 2
(*) log ( 5) log ( 2) 3 log ( 5)( 2) 3 ( 5)( 2) 8x x x x x x- + + = - + = - + =� � �
(nhan)
(loai)
2 2
6
2 5 10 8 3 18 0 3
x
x x x x x x
￲=
￲
+ - - = - - =� � ￲=
￲
￲
a
I
M
H
C '
B '
A
B
C
A '
￲ V y, ph ng trình có nghi m duy nh t: ậ ươ ệ ấ x = 6
ln 2
3 2 2 ln 2 0
ln 2 ln 2 2 ln 2 0
0 0 0
1( ) 2 2 2
x x
x x x
x
e e e e
I dx e e dx e e e
e
- - -
� � � � � �
+� � �
� � �
� � �
� � �
= = + = - = - - -
� � �
� � �
� � �
� � � � � �
� �
￲ V y, ậ
1
ln 4 ln 2
1 4 1 1
1 1 2
2 2 2 2 2
e
I e
� � � �
￲
￲￲
￲
￲
￲￲
= - - - = - - + =
￲ ￲
￲￲
￲
� �
� � � �
￲ Hàm s ố
3 2 2 3
1 1
x x
yx x
- - +
= =
+ +
liên t c trên đo nụ ạ
[1; 4]
￲
2
50, [1; 4]
( 1)
y x
x
-
￲= < " ￲
+
￲
1
(1) 2
f=
và
(4) 1f= -
￲ Trong 2 k t qu trên, s –1 nh nh t, s ế ả ố ỏ ấ ố
1
2
l n nh t.ớ ấ
￲ V y, ậ
khi khi
[1;4] [1;4]
1
min 1 4 , max 1
2
y x y x= - = = =
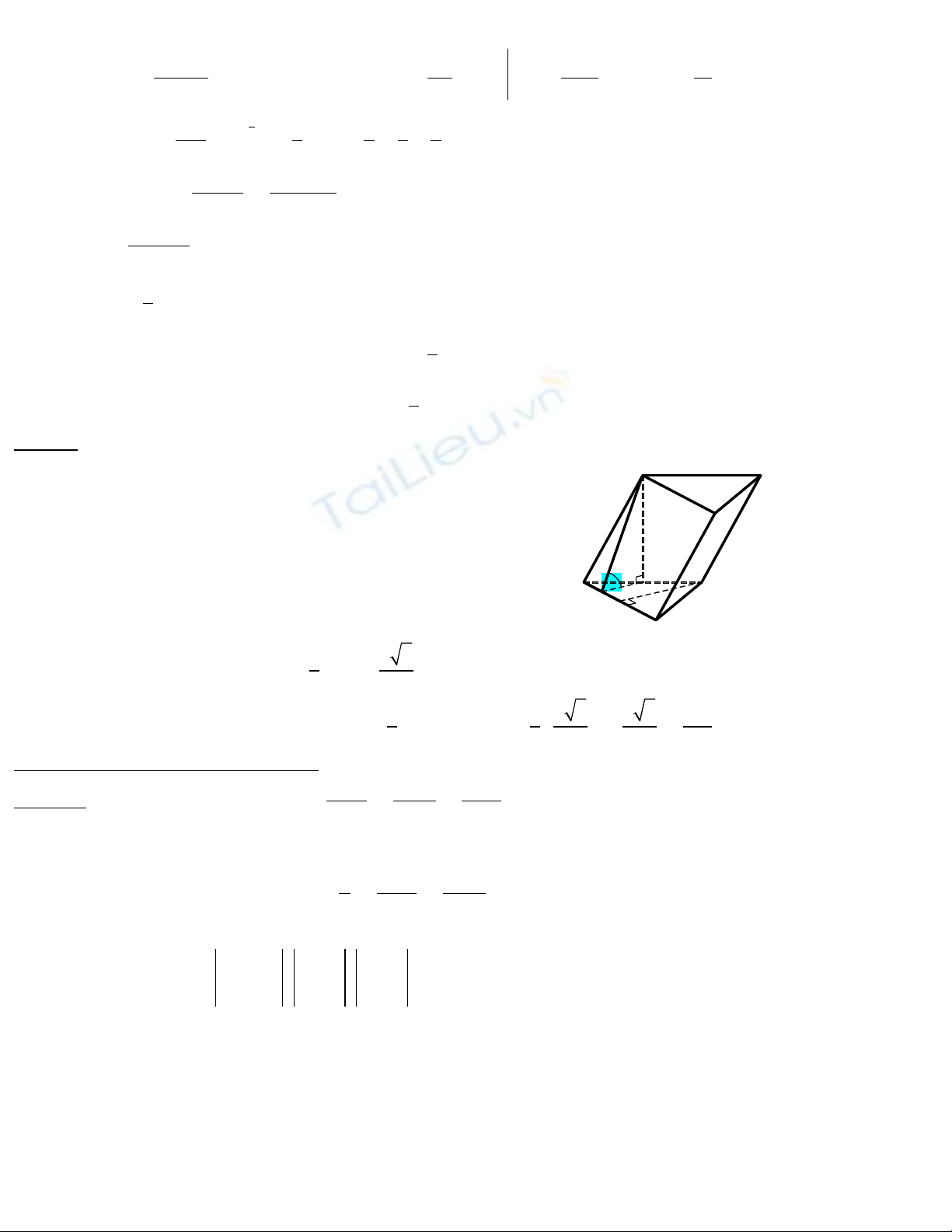
Câu III
￲ G i ọH,M,I l n l t là trung đi m các đo n ầ ượ ể ạ AB,AC,AM
￲ Theo gi thi t, ả ế
( ),A H A BC BM A C
￲^ ^
Do IH là đ ng trung bình tam giác ườ ABM nên
||IH BM IH A C^�
￲ Ta có,
,A C IH A C A H A C IA
￲ ￲
^ ^ ^�
Suy ra góc gi a ữ
( )A BC
và
( )A CC A
￲ ￲
là
ﾡ
o
45A IH
￲=
￲
o
1 3
. t an 45 2 4
a
A H IH IH MB
￲= = = =
￲ V y, th tích lăng tr là: ậ ể ụ
3
1 1 3 3 3
. . .
2 2 2 2 8
a a a
V B h BM A C A H a
￲
= = = =���
(đvdt)
THEO CH NG TRÌNH CHU NƯƠ Ẩ
Câu IVa:
(0;1; 4), (1; 0; 5)A B- -
và
1 4 1
:1 4 2
x y z- - -
= =D- -
￲ Đ ng th ng ườ ẳ AB đi qua đi m ể
(0;1; 4)A-
, có vtcp
(1; 1; 1)u A B= = - -
uuur
r
￲ PTCT c a đ ng th ng ủ ườ ẳ AB là:
1 4
1 1 1
x y z- +
= =
- -
￲ Đ ng th ng ườ ẳ
D
đi qua đi m ể
(1; 4;1)M
, có vtcp
(1; 4; 2)u￲= - -
r
￲ Ta có,
1 1 1 1 1 1
[ , ] ; ; ( 2;1; 3)
4 2 2 1 1 4
u u
� �
- - - - ￲
￲￲
￲
￲= = - -
￲
￲￲
￲- - - - ￲
￲
￲
� �
r r
(1; 3; 5) [ , ]. 1.1 1.3 3.5 13 0A M u u A M
￲
= = - + - = -� �
uuuur uuuur
r r
￲ V y, ậAB và
D
chéo nhau.
M t ph ng (ặ ẳ P) ch a hai đi m ứ ể A,B đ ng th i song song v i đ ng th ng ồ ờ ớ ườ ẳ
D
￲ Đi m trên mp(ểP):
(0;1; 4)A-
￲ Vì (P) ch a ứA,B và song song v i ớ
D
nên có vtpt:
[ , ] ( 2;1; 3)n u u ￲
= = - -
r r r
￲ PTTQ c a (ủP):
2( 0) 1( 1) 3( 4) 0 2 3 13 0x y z x y z- - + - - + = - + + =�
￲ Kho ng cách gi a ả ữ AB và
D
b ng: ằ
2 2 2
2.1 4 3.1 13 14
( ,( )) 14
14
2 ( 1) 3
d M P - + +
= = =
+ - +
Câu Va: Tính di n tích hình ph ng gi i h n b i: ệ ẳ ớ ạ ở
2
12 36y x x= - +
và
2
6y x x= -
￲ Cho
2 2 2
12 36 6 2 18 36 0 3, 6x x x x x x x x- + = - - + = = =� �
￲ Di n tích c n tìm là: ệ ầ
6 6
2 2
3 3
2 18 36 (2 18 36)S x x dx x x dx= - + = - +
� �
6
3
2
3
29 36 9 9
3
xx x
� �
￲
￲￲
￲
= - + = - =
￲
￲￲
� �
(đvdt)
THEO CH NG TRÌNH NÂNG CAOƯƠ
Câu IVb:
￲
1
D
đi qua đi m ể
1
(1; 1;2)M-
, có vtcp
1
(1; 1; 0)u= -
r
2
D
đi qua đi m ể
2
(3;1; 0)M
, có vtcp
2
( 1;2;1)u= -
r
￲ Ta có,
1 2
1 0 0 1 1 1
[ , ] ; ; ( 1; 1;1)
2 1 1 1 1 2
u u
� �
- - ￲
￲￲
￲
= = - -
￲
￲￲
￲- - ￲
￲
￲
� �
r r
1 2
(2;2; 2)M M = -
uuuuuur
1 2 1 2
[ , ]. 1.2 1.2 1.( 2) 6 0u u M M = - - + - = -� �
uuuuuur
r r
￲ Suy ra,
1
D
và
2
D
chéo nhau.
￲ mp(P) ch a ứ
1
D
và song song
2
D
nên đi qua
1
(1; 1;2)M-
, có vtpt
1 1 2
[ , ] ( 1; 1;1)n u u= = - -
r r r
￲ V y, PTTQ mp(ậP):
1( 1) 1( 1) 1( 2) 0 2 0x y z x y z- - - + + - = + - + =�
￲ Vì
1 2
,A B�D �D
nên to đ c a chúng có d ng: ạ ộ ủ ạ
(1 ; 1 ;2), (3 ;1 2 ; ) (2 ;2 2 ; 2)A a a B b b b A B a b a b b+ - - - + = - - + + -�uuur
￲ AB ng n nh t ắ ấ
￲
AB là đ ng vuông góc chung c a ườ ủ
1
D
và
2
D
1
2
. 0 (2 ).1 (2 2 ).( 1) ( 2).0 0
(2 ).( 1) (2 2 ).2 ( 2).1 0
. 0
2 2 2 0 2 3 0 0
2 4 2 4 2 0 3 6 0 0
A B u a b a b b
a b a b b
A B u
a b a b a b a
a b a b b a b b
￲
￲￲
￲
= - - + + + - + - =
￲￲
￲
� �
� �
� � - - - + + + + - =
=
� �
￲
￲
￲
� � �
� � �
- - - - - = - - = =
� � �
� � �
� � �
� � �
- + + + + + + - = + = =
� � �
� � �
uuur r
uuur r
￲ V y, ậ
(1; 1; 2), (3;1; 0)A B-
Câu Vb:
2
0z Bz i+ + =
có t ng bình ph ng hai nghi m b ng ổ ươ ệ ằ
4i-
￲ Gi s ả ử z1 và z2 là 2 nghi m ph c c a ph ng trình trên. D a vào công th c nghi m ph ng trình b cệ ứ ủ ươ ự ứ ệ ươ ậ
hai, ta suy ra:
va
1 2 1 2
.
2
b c
z z B z z i
a a
+ = - = - = =
￲ Theo gi thi t, ả ế
2 2 2 2 2
1 1 1 2 1 2
4 ( ) 2 4 2 4 2z z i z z z z i B i i B i+ = - + - = - - = - = -� � �
2 2
(1 ) (1 )B i B i= - = -� � �
￲ V y, ậ
(1 )B i= ￲ -
Hiendvtiger.violet.vn