L p:ớĐ KI M TRA 1 TI T MÔN TOÁN L N 2 Ề Ể Ế Ầ
KH I 10 ỐNC (NH:2013-2014)
------------------
H và tên:ọ
…………………………….
Bài 1: (3.0đ)
1/ Tìm t p xác đ nh c a các hàm s sau: ậ ị ủ ố
2
2
2 1 3 7
a) b) 4
2 1
x x x
y y x x
x
− − − −
= = −
−
2/ Xét tính ch n – l c a hàm s sau: ẵ ẻ ủ ố
4 2
2 3y x x= − +
Bài 2: (4.0đ) Cho hàm s ố
2
4 3y x x= − + −
có đ th (P)ồ ị
1/ Kh o sát s bi n thiên và v đ th (P). ả ự ế ẽ ồ ị
2/ Tìm m đ đ th (P) và đ ng th ng d:ể ồ ị ườ ẳ
3y x m= +
có 2 giao đi m.ể
Bài 3: (3.0đ)
1/ Xác đ nh hàm s ị ố
( )
0y ax b a= +
, bi t đ th c a nó song song v i đ ngế ồ ị ủ ớ ườ
th ng ẳ
7y x= −
và c t tr c tung t i đi m có tung đ b ngắ ụ ạ ể ộ ằ 2013.
2/ Xác đ nh Parabol (P): ị
( )
2
0y ax bx c a= + +
đ t giá tr l n nh t b ng ạ ị ớ ấ ằ
khi
3
2
x=
và nh n giá tr ậ ị
2y= −
khi
3x=
.
L p:ớĐ KI M TRA 1 TI T MÔN TOÁN L N 2 Ề Ể Ế Ầ
KH I 10 ỐNC (NH:2013-2014)
------------------
H và tên:ọ
…………………………….
Bài 1: (3.0đ)
1/ Tìm t p xác đ nh c a các hàm s sau: ậ ị ủ ố
2
2
2 2 5
a) 2 2 3 b) 4
x x
y x x y x
+ − −
= − − + = −
2/ Xét tính ch n – l c a hàm s sau: ẵ ẻ ủ ố
33y x x= +
Bài 2: (4.0đ) Cho hàm s ố
2
4 3y x x= + +
có đ th (P)ồ ị
1/ Kh o sát s bi n thiên và v đ th (P). ả ự ế ẽ ồ ị
2/ Tìm m đ đ th (P) và đ ng th ng d:ể ồ ị ườ ẳ
5y x m= −
không có giao đi m.ể
Bài 3: (3.0đ)
1/ Xác đ nh hàm s ị ố
( )
0y ax b a= +
, bi t đ th c a nó song song v i đ ngế ồ ị ủ ớ ườ
th ng ẳ
3 1y x= −
và c t tr c hoành t i đi m có hoành đ b ngắ ụ ạ ể ộ ằ 2014.
2/ Xác đ nh Parabol (P): ị
( )
2
0y ax bx c a= + +
đ t giá tr nh nh t b ng ạ ị ỏ ấ ằ
3
2
−
khi
3
2
x=
và nh n giá tr ậ ị
1y= −
khi x = 2.
\
Đ : 1ề
Đ : 2ề
Đáp án:
Đ 1:ề
Bài 1 (3.0đ)
[ ]
{ }
2
1
2 1 0 2
1;
2
1 0 1
7 0 7
0; 4
4 0
1;7 \ 4
x x
D
x x
x x
x x
x x
D
− > >�
� �
= +
� �
� �
−
� �
− �
� �
� �
−
=
1a) Hs x� khi:
TX�:
1b) Hs x� khi
TX�:
( ) ( ) ( )
( )
4 2
4 2
2)
2 3
2 3
D
x D x D
f x x x
x x f x
=
∀ −�� �
− = − − − +
= − + =
ﾡ TX�:
Va�y ha�m so� �a� cho la� ha�m so� cha�n.
Bài 2: (4.0đ)
1) + TXĐ :
ﾡ
+ Tr c đ i x ng:ụ ố ứ
2x=
+ Đ nh ỉ
( )
2;1I
+
1 0a= − <
nên hàm s ĐB trên kho ngố ả
( )
; 2−
và hàm s ĐB trên kho ng ố ả
( )
2; +
.
* BBT x
−
2
+
y 1
−
−
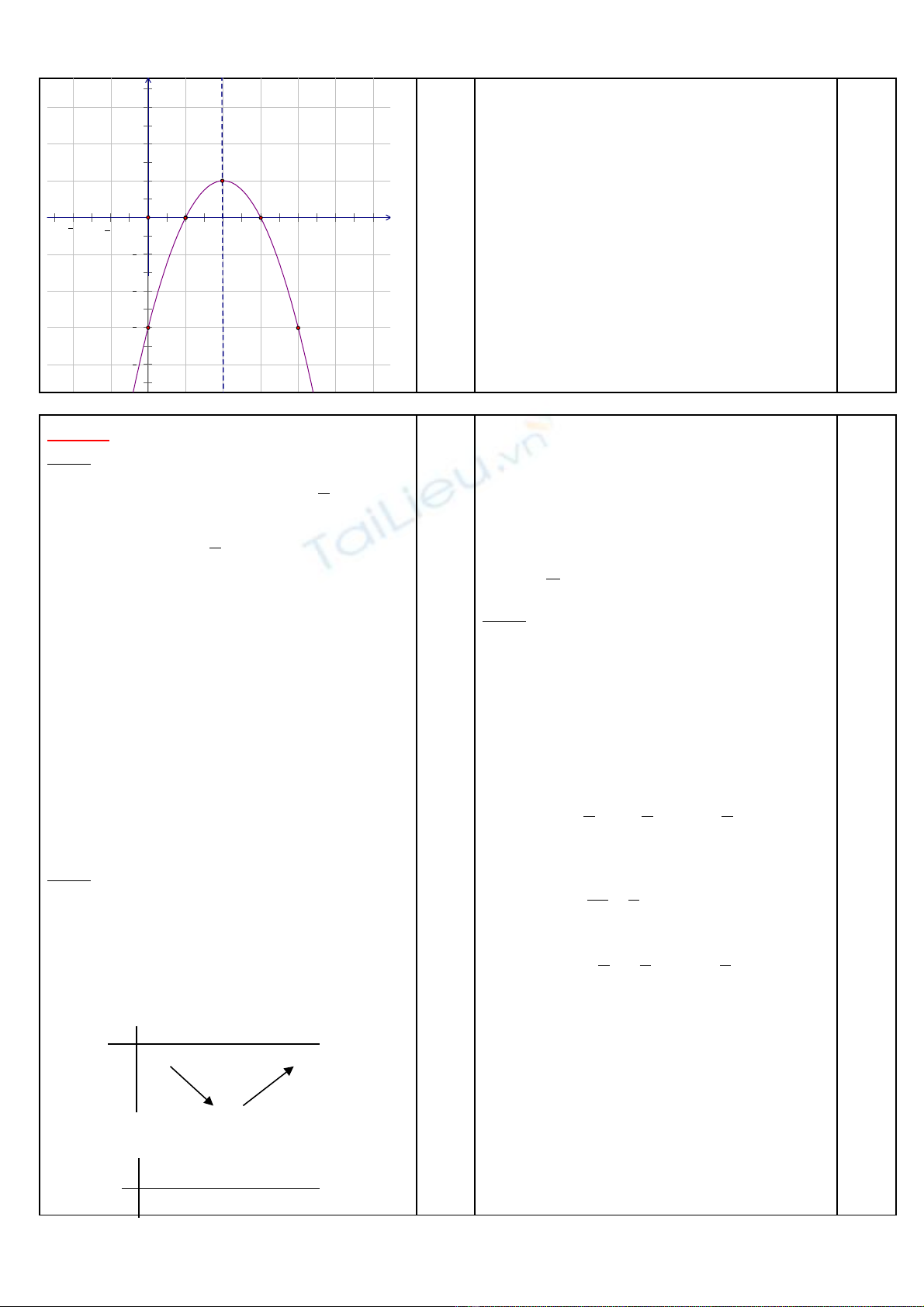
+ Đ thồ ị :
BGT: x 0 1 2 3 4
y -3 0 1 0 -3
0.5
0.5
0.5
0.5
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
1.25
2/ PTHĐ giao đi m c a (P) và d là: ể ủ
2
2
4 3 3
3 0
1 4 12 4 11
4 11 0
11
4
x x x m
x x m
m m
m
m
− + − = +
− + + =�
∆ = − − = − −
∆ = − − >
< −�
co�
�e� (p) va� d co� 2 giao �ie�m th�
Bài 3: (3.0đ)
1) Do
y ax b= +
song song v i đt ớ
7y x= −
nên h/s có dang:
( )
7 0y x b b
= − +
Đ th đi qua đi m ồ ị ể
( )
0; 2013
suy ra: b = 2013
V y hàm s c n tìm là:ậ ố ầ
7 2013y x= − +
2) Theo đ bài ta có:ề
2
2
3 3 1
2 2 4
3 3 2
3
2 2
9 3 1
4 2 4
9 3 2
3 0
1 0
3
2
a b c
a b c
b
a
a b c
a b c
a b
a
b
c
� � + + =
� �
� �
+ + = −
− =
+ + =
+ + = −�+ =
= − <
=�= −
V y hàm s c n tìm làậ ố ầ :
2
3 2y x x= − + −
0.25
0.25
0.5
0.25
0.25
0.5
0.5
0.5
0.5
0.25
0.5
0.25
3
2
1
1
2
3
4
2
2
4
6
x
y
(P)
x
=
3
1
1
I
O
Đ 2:ề
Bài 1 (3.0đ)
(
]
{ }
2
2
2 3 0 3
2;
3
2 0 2
5 0 5
2; 2
4 0
2;5 \ 2
x x
D
x x
x x
x x
x
D
− + > >�
� �
= +
� �
� �
+ −
� �
− �
� �
� � −
−
= −
1a) Hs x� khi:
TX�:
1b) Hs x� khi
TX�:
( ) ( ) ( )
( )
( )
33
3
2)
3 3
3
D
x D x D
f x x x x x
x x f x
=
∀ −�� �
− = − + − = − −
= − + = −
ﾡ TX�:
Va�y ha�m so� �a� cho la� ha�m so� le�.
Bài 2: (4.0đ)
1+ TXĐ :
ﾡ
+ Tr c đ i x ng:ụ ố ứ
2x= −
+ Đ nh ỉ
( )
2;1I−
+
1 0a= >
nên hàm s NB trên kho ngố ả
( )
;1−
và hàm s ĐB trên kho ng ố ả
( )
1;+
.
* BBT x
−
-2
+
y
+
+
1
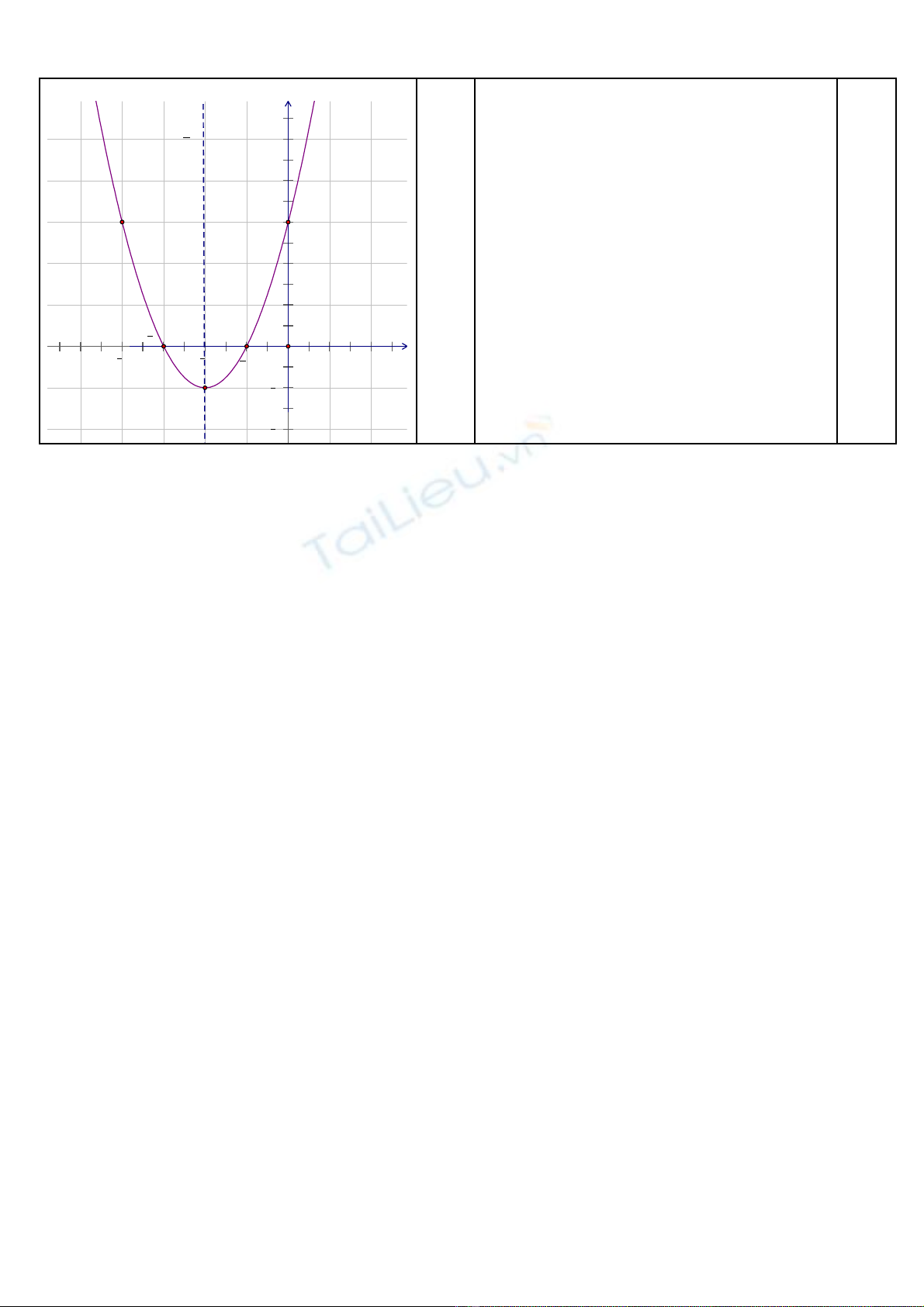
+ Đ thồ ị :
BGT: x -4 -3 -2 -1 0
y 3 0 1 0 3
0.5
0.5
0.5
0.5
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
2/ PTHĐ giao đi m c a (P) và d là: ể ủ
2
2
4 3 5
3 0
1 12 4 4 11
4 11 0
11
4
x x x m
x x m
m m
m
m
+ + = −
− + + =�
∆ = − − = − −
∆ = − − <
> −�
co�
�e� (p) va� d kho�ng co� giao �ie�m th�
Bài 3: (3.0đ)
1) Do
y ax b= +
song song v i đt ớ
3 1y x= −
nên h/s có dang:
( )
3 1y x b b
= + −
Đ th đi qua đi m ồ ị ể
( )
2014;0
suy ra: b = -6042
V y hàm s c n tìm là:ậ ố ầ
3 6042y x= −
2) Theo đ bài ta có:ề
2
2
3 3 3
2 2 2
2 2 1
3
2 2
9 3 3
4 2 2
4 2 1
3 0
2 0
6
3
a b c
a b c
b
a
a b c
a b c
a b
a
b
c
� � + + = −
� �
� �
+ + = −
− =
+ + = −
+ + = −�+ =
= >
= −�=
V y hàm s c n tìm làậ ố ầ :
2
2 6 3y x x= − +
0.25
0.25
0.5
0.25
0.25
0.5
0.5
0.5
0.5
0.25
0.5
0.25
5
4
3
2
1
1
2
4
2
2
x
y
(P)
3
x
=
2
1
1
O
I
1.25