Đề ôn kiểm tra định kỳ giữa học kỳ 2, năm học 2020-2021
TRƯỜNG .........................
ĐỀ ÔN SỐ 1
ĐỀ KIỂM TRA ĐỊNH KỲ GIỮA HK 2, NĂM HỌC 2020-2021
MÔN TOÁN-THPT
Thời gian làm bài 90 phút, không tính thời gian giao đề
Câu 1. Cho
π
2
Z
0
f(x)dx= 5. Tính I=
π
2
Z
0
[f(x) + 2 sin x]dx= 5.
AI= 5 + π
2.BI= 5 + π.CI= 7.DI= 3.
Câu 2. Trong không gian với hệ trục Oxyz, cho mặt phẳng (P) : 3x−z+ 2 = 0. Vectơ nào dưới đây
là một vectơ pháp tuyến của (P)?
A#»
n3= (3; −1; 0).B#»
n1= (3; −1; 2).C#»
n2= (3; 0; −1).D#»
n4= (−1; 0; −1).
Câu 3. Cho F(x)là một nguyên hàm của hàm số f(x) = 1
x−2,biết F(1) = 2.Giá trị của F(0)
bằng
A2 + ln 2.Bln 2.Cln (−2).D2 + ln (−2).
Câu 4. Tính tích phân I=
0
Z
−1
(2x+ 1) dx.
AI= 2.BI=−1
2.CI= 1.DI= 0.
Câu 5. Nguyên hàm của hàm số y= e2x−1là
A2e2x−1+C.B1
2e2x−1+C.Ce2x−1+C.D1
2ex+C.
Câu 6. Trong không gian với hệ toạ độ Oxyz cho mặt cầu (S) : x2+ (y+ 2)2+ (z−2)2= 8. Tính
bán kính Rcủa (S).
AR= 4.BR= 8.CR= 64.DR= 2√2.
Câu 7. Cho F(x)là một nguyên hàm của hàm số f(x) = ex+2xthỏa mãn F(0) = 3
2. Tìm F(x).
AF(x) = ex+x2+3
2.BF(x) = ex+x2+1
2.
CF(x) = ex+x2+5
2.DF(x) = 2ex+x2−1
2.
Câu 8. Biết
2
Z
0
2xln (x+ 1) dx=aln b, với a, b ∈N∗,blà số nguyên tố. Tính 6a+ 7b.
A6a+ 7b= 25.B6a+ 7b= 42.C6a+ 7b= 39.D6a+ 7b= 33.
Câu 9. Trong không gian với hệ tọa độ Oxyz, cho A(1; 3; 2),B(3; −1; 4). Tìm tọa độ trung điểm I
của AB.
AI(4; 2; 6).BI(−2; −1; −3).CI(2; 1; 3).DI(2; −4; 2).
Câu 10. Trong không gian với hệ trục tọa độ Oxyz cho M(4; 5; 6). Hình chiếu của Mxuống mặt
phẳng (Oyz)là M′. Xác định tọa độ M′.
AM′(4; 5; 0).BM′(4; 0; 0).CM′(4; 0; 6).DM′(0; 5; 6).
Câu 11.
2
Z
1
dx
2x+ 3 bằng
A1
2ln 35.B1
2ln 7
5.Cln 7
5.D2 ln 7
5.
Đề ôn GHKII-12, năm học 2020-2021 Trang 1
Biên soạn & sưu tầm: Những nẻo đường phù sa
Câu 12. Tìm nguyên hàm của hàm số f(x) = 7x.
AZ7xdx=7x
ln 7 +C.BZ7xdx= 7xln 7 + C.
CZ7xdx=7x+1
x+ 1 +C.DZ7xdx= 7x+1 +C.
Câu 13. Cho
m
Z
03x2−2x+ 1dx= 6. Giá trị của tham số m thuộc khoảng nào sau đây?
A(−∞; 0).B(−1; 2).C(−3; 1).D(0; 4).
Câu 14. Trong không gian với hệ trục tọa độ Oxyz, cho #»
a= (2; −3; 3),#»
b= (0; 2; −1),#»
c= (3; −1; 5).
Tìm tọa độ của vectơ #»
u= 2#»
a+ 3
#»
b−2#»
c.
A(−2; 2; −7).B(−2; −2; 7).C(10; −2; 13).D(−2; 2; 7).
Câu 15. Cho hàm số f(x)liên tục trên R. Gọi Slà diện tích hình phẳng giới hạn bởi các đường
y=f(x), y = 0, x =−1, x = 2. Mệnh đề nào dưới đây đúng?
AS=
1
Z
−1
f(x)dx−
2
Z
1
f(x)dx.BS=
1
Z
−1
f(x)dx+
2
Z
1
f(x)dx.
CS=−
1
Z
−1
f(x)dx+
2
Z
1
f(x)dx.DS=−
1
Z
−1
f(x)dx−
2
Z
1
f(x)dx.
Câu 16. Biết
2
Z
1
dx
(x+ 1) (2x+ 1) =aln 2 + bln 3 + cln 5. Khi đó giá trị a+b+cbằng
A0.B1.C−3.D2.
Câu 17. Trong không gian Oxyz, cho mặt cầu (S) : x2+y2+z2+ 2x−4y−2z−3 = 0.Tọa độ tâm
Icủa mặt cầu (S)là:
A(2; −4; −2).B(−2; 4; 2).C(1; −2; −1).D(−1; 2; 1).
Câu 18. Gọi đường cong (OAB)là hình phẳng giới hạn bởi các đồ thị hàm số y= 2x2,y= 3 −x,
y= 0 (tham khảo hình vẽ).
x
y
O
y= 2x2
y= 3 −x
A
B
Diện tích của (OAB)bằng
A8
3.B5
3.C4
3.D10
3.
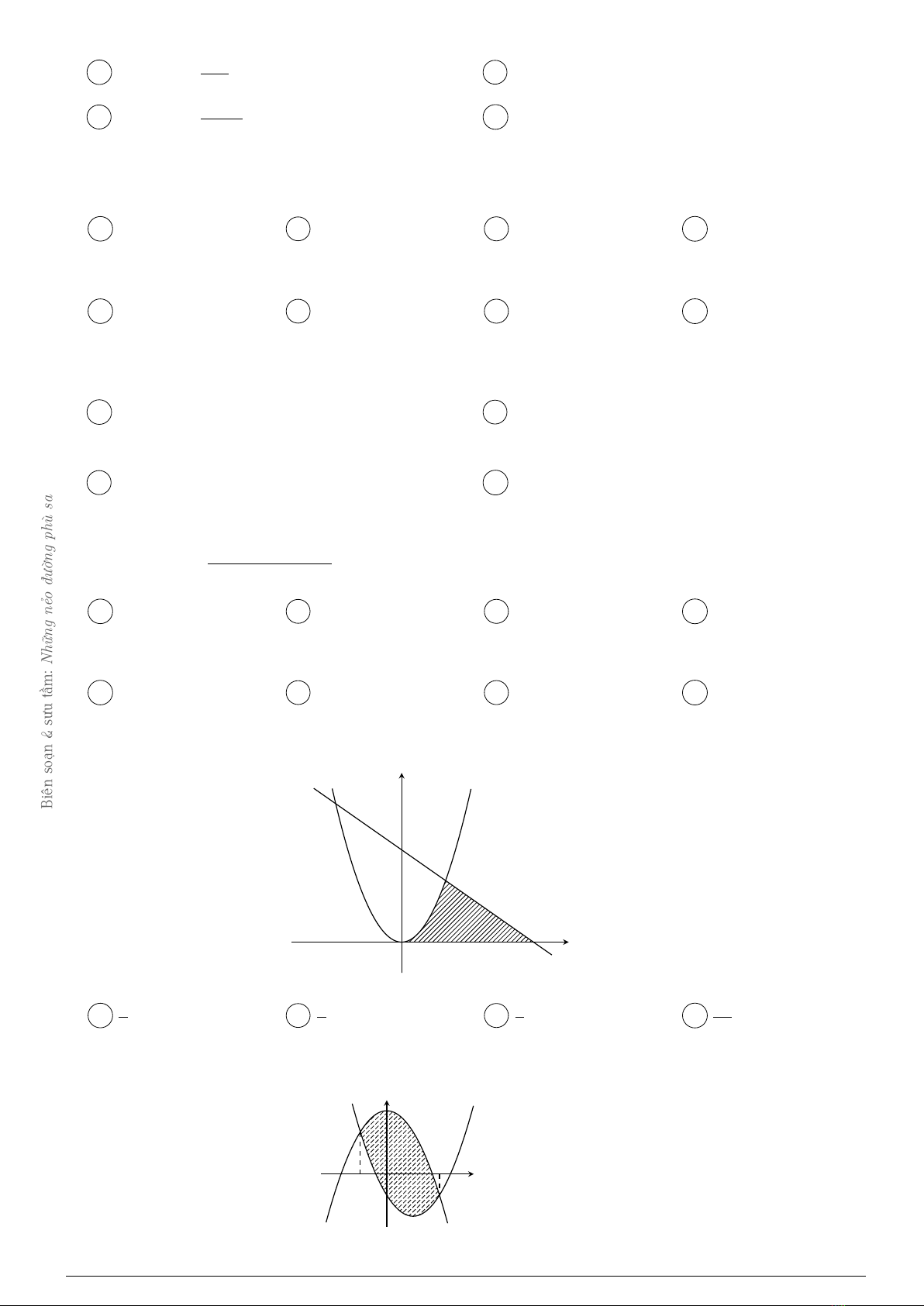
Câu 19. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới
đây?
x
y
O
y=x2−2x−1
y= 3 −x
A
B
−1
2
Đề ôn GHKII-12, năm học 2020-2021 Trang 2
Đề ôn kiểm tra định kỳ giữa học kỳ 2, năm học 2020-2021
A
2
Z
−1−2x2+ 2x+ 4dx.B
2
Z
−1
(2x−2) dx.
C
2
Z
−1
(−2x+ 2) dx.D
2
Z
−12x2−2x−4dx.
Câu 20. Tích phân
1
Z
0
(x−2) e2xdxbằng
A5−3e2
4.B−5−3e2
4.C5−3e2
2.D5 + 3e2
4.
Câu 21. Trong không gian Oxyz cho hai điểm I(1; 1; 1) và A(1; 2; 3). Phương trình mặt cầu có tâm
Ivà đi qua Alà
A(x−1)2+ (y−1)2+ (z−1)2= 25.B(x+ 1)2+ (y+ 1)2+ (z+ 1)2= 29.
C(x+ 1)2+ (y+ 1)2+ (z+ 1)2= 5.D(x−1)2+ (y−1)2+ (z−1)2= 5.
Câu 22. Cho tích phân I=
4
Z
0
f(x)dx= 32.Tính tích phân J=
2
Z
0
f(2x)dx.
AJ= 8.BJ= 16.CJ= 32.DJ= 64.
Câu 23. Cho tích phân
2
Z
1
f(x)dx=a. Hãy tính tích phân I=
1
Z
0
xf x2+ 1dxtheo a.
AI= 2a.BI=a
2.CI=a
4.DI= 4a.
Câu 24. Cho
2
Z
−2
f(x)dx= 1,
4
Z
−2
f(t)dt=−4. Tính
4
Z
2
f(y)dy.
AI=−3.BI= 3.CI= 5.DI=−5.
Câu 25. Giả sử I=
π
4
Z
0
sin 3xdx =a+b√2
2(a, b ∈Q). Khi đó giá trị của a−blà
A−1
6.B−3
10.C1
5.D−1
6.
Câu 26. Cho
6
Z
0
f(x)dx= 12. Tính I=
2
Z
0
f(3x)dx.
AI= 36.BI= 6.CI= 5.DI= 4.
Câu 27. Trong không gian với hệ toạ độ Oxyz, cho mặt phẳng (P): 3x+ 4y+ 2z= 0 và điểm
A(1; −2; 3). Tính khoảng cách dtừ Ađến (P).
Ad=5
√29.Bd=5
9.Cd=5
29.Dd=√5
3.
Câu 28. Trong không gian cho hệ trục toạ độ Oxyz, cho ba điểm A(1; −2; 3) , B (−1; 2; 5) , C (0; 0; 1).
Tìm toạ độ trọng tâm Gcủa tam giác ABC.
AG(0; 0; 9).BG(0; 0; 3).CG(0; 0; 1).DG(−1; 0; 3).
Câu 29. Trong không gian với hệ toạ độ Oxyz, cho điểm M(3; −1; −2) và mặt phẳng (α) : 3x−
y+ 2z+ 4 = 0.Phương trình nào dưới đây là phương trình mặt phẳng đi qua Mvà song song với
(α)?
A3x−y−2z+ 6 = 0.B3x−y+ 2z−6 = 0.
C3x−y+ 2z+ 6 = 0.D3x+y+ 2z−14 = 0.
Đề ôn GHKII-12, năm học 2020-2021 Trang 3
Biên soạn & sưu tầm: Những nẻo đường phù sa
Câu 30. Cho hàm số f(x). Biết f(0) = 4 và f′(x) = 2 sin2x+ 3,∀x∈R, khi đó
π
4
Z
0
f(x)dxbằng
Aπ2+ 8π−2
8.B3π2+ 2π−3
8.Cπ2−2
8.Dπ2+ 8π−8
8.
Câu 31. Cho hàm số f(x)liên tục, có đạo hàm trên [−1; 2] , f (−1) = 8; f(2) = −1. Tích phân
2
Z
−1
f′(x)dxbằng
A9.B1.C−9.D7.
Câu 32. Nguyên hàm của hàm số f(x) = x4+x2là
A4x3+ 2x+C.Bx5+x3+C.Cx4+x2+C.D1
5x5+1
3x3+C.
Câu 33. .Cho hàm số y=f(x)xác định và liên tục trên đoạn [a;b]. Diện tích hình phẳng giới hạn
bởi đồ thị hàm số y=f(x), trục hoành và hai đường thẳng x=a;x=bđược tính theo công thức
AS=−
b
Z
a
f(x)dx.BS=
b
Z
a
|f(x)|dx.CS=
a
Z
b
|f(x)|dx.DS=
b
Z
a
f(x)dx.
Câu 34. Cho
2
Z
−1
f(x)dx= 2 và
2
Z
−1
g(x)dx=−1. Tính I=
2
Z
−1
[x+ 2f(x)−3g(x)] dx.
AI=11
2.BI=17
2.CI=5
2.DI=7
2.
Câu 35. Cho hàm số f(x)liên tục trên đoạn [0; 10] và
10
Z
0
f(x)dx= 7;
6
Z
2
f(x)dx= 3. Tính P=
2
Z
0
f(x)dx+
10
Z
6
f(x)dx.
AP= 10.BP= 4.CP= 7.DP=−4.
Câu 36. Thể tích khối tròn xoay khi quay hình phẳng (H)xác định bởi các đường y=1
3x3−x2,y=
0,x= 0 và x= 3 quanh trục Ox là
A71
35.B81
35.C81π
35 .D71π
35 .
Câu 37. Biết
2
Z
1
f(x) dx= 2 và
2
Z
1
g(x) dx= 6, khi đó
2
Z
1
[f(x)−g(x)] dxbằng
A4.B−8.C8.D−4.
Câu 38. Giá trị của
π
2
Z
0
sin xdx bằng
A0. Bπ
2.C1. D-1.
Câu 39. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y= 4x−x2và trục Ox
A32
3.B31
3.C34
3.D11.
Câu 40. Trong không gian Oxyz, cho mặt cầu (S) : x2+y2+z2+ 2x−2z−7 = 0. Bán kính của
mặt cầu đã cho bằng
A9.B3.C√15.D√7.
Đề ôn GHKII-12, năm học 2020-2021 Trang 4
Đề ôn kiểm tra định kỳ giữa học kỳ 2, năm học 2020-2021
Câu 41. Tìm nguyên hàm của hàm số f(x) = 1
5x−2.
AZdx
5x−2=−1
2ln |5x−2|+C.BZdx
5x−2= ln |5x−2|+C.
CZdx
5x−2=1
5ln |5x−2|+C.DZdx
5x−2= 5 ln |5x−2|+C.
Câu 42. TínhZ(x−sin 2x)dx.
Ax2
2+ cos 2x+C.Bx2
2+cos 2x
2+C.Cx2
2+ sin x+C.Dx2+cos 2x
2+C.
Câu 43. Trong không gian với hệ trục tọa độ Oxyz, cho hai vectơ #»
a= (2; 1; 0) và #»
b= (−1; 0; −2).Tính
cos Ä#»
a ,
#»
bä.
Acos Ä#»
a ,
#»
bä=2
25.Bcos Ä#»
a ,
#»
bä=2
5.Ccos Ä#»
a ,
#»
bä=−2
5.Dcos Ä#»
a ,
#»
bä=−2
25.
Câu 44. Tính tích phân I=
e
Z
1
xln xdx:
AI=1
2.BI=e2−1
4.CI=e2−2
2.DI=e2+ 1
4.
Câu 45. Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1; 0; 3),B(2; 3; −4),C(−3; 1; 2).
Tìm tọa độ điểm Dsao cho ABCD là hình bình hành.
AD(4; −2; 9).BD(−4; 2; 9).CD(4; 2; −9).DD(−4; −2; 9).
Câu 46. Trong không gian với hệ tọa độ Oxyz, phương trình nào dưới đây là phương trình mặt
phẳng đi qua điểm M(1; 2; −3) và có một vectơ pháp tuyến #»
n= (1; −2; 3).
Ax−2y−3z+ 6 = 0.Bx−2y+ 3z+ 12 = 0.
Cx−2y+ 3z−12 = 0.Dx−2y−3z−6 = 0.
Câu 47. Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1; 0; 0),B(0; 0; 1),C(2; 1; 1).
Diện tích của tam giác ABC bằng:
A√11
2.B√7
2.C√5
2.D√6
2.
Câu 48. Cho
1
Z
0
Å1
x+ 1 −1
x+ 2ãdx=aln 2 + bln 3 với a, b là các số nguyên. Mệnh đề nào dưới đây
đúng?
Aa−2b= 0.Ba+ 2b= 0.Ca+b=−2.Da+b= 2.
Câu 49. Một ô tô đang chạy với tốc độ 10 (m/s )thì người lái đạp phanh,từ thời điểm đó ô tô chuyển
động chậm dần đều với v(t) = −5t+ 10 (m/s ), trong đó tlà khoảng thời gian tính bằng giây,kể từ lúc
bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn,ô tô còn di chuyển bao nhiêu mét.
A8m.B20m.C5m.D10m.
Câu 50. Cho hàm số f(x)xác định trên R\ß1
3™thoả mãn f′(x) = 3
3x−1,f(0) = 1,fÅ2
3ã= 2.
Giá trị của biểu thức f(−1) + f(3) bằng
A3 + 5 ln 2.B−2 + 5 ln 2.C4 + 5 ln 2.D2 + 5 ln 2.
——————Hết——————
Đề ôn GHKII-12, năm học 2020-2021 Trang 5