
1/6 - Mã đề 166
TRƯỜNG THPT DUYÊN HẢI
TỔ TOÁN - TIN
(Đề thi có 06 trang)
ĐỀ THI HỌC KỲ II
NĂM HỌC 2017 - 2018
MÔN TOÁN – Khối lớp 12
Thời gian làm bài : 90 phút
(khôn
g
kể thời
g
ian phát đề)
Họ và tên học sinh :..................................................... Số báo danh : ...................
Câu 1. Gọi H là hình phẳng giới hạn bởi đồ thị hàm số
x
yxe và các đường thẳng 1, 2, 0xx y
.
Tính thể tích V của khối tròn xoay thu được khi quay hình H xung quanh trục Ox.
A. 2
Ve
` B. 2
2Ve
C. 2Ve
D.
2Ve
Câu 2. Biết 12
;zz
( với 1
z là số phức có phần ảo dương ) là hai nghiệm phức của phương trình
26140zz
. Tìm 1
2
z
z.
A. 235
77
i B. 235
77
i C. 235
77
i D. 235
77
i
Câu 3. Cho hàm số f(x) có đạo hàm trên đoạn
0; 2 và
03;27ff . Tính
2
0
I
f
xdx
.
A. 4I B. 4I C. 10I D. 10I
Câu 4. Trong không gian Oxyz cho mặt cầu
222
:1427Sx y z .Tìm tọa độ tâm I và bán
kính R của mặt cầu.
A.
1; 4; 2 ; 7IR B.
1; 4; 2 ; 7IR
C.
1; 4; 2 ; 7IR D.
1; 4; 2 ; 7IR
Câu 5. Tìm số phức 52
3
i
wi
.
A. 13 11
10 10 i B. 13 11
10 10 i C. 13 11
10 10 i D. 13 11
10 10 i
Câu 6. Cho số phức zabi thoả mãn
2
2211215iz z i i . Tìm ab .
A. 1 B. 1 C. 3 D. 7
Câu 7. Tìm phương trình mặt cầu (S) có tâm
2;3 1Ivà tiếp xúc với mặt phẳng
:2 2 5 0xy z
.
A.
222
:2 3 14Sx y z B.
222
:2 3 12Sx y z
C.
222
:2 3 12Sx y z
D.
222
:2 3 14Sx y z
Câu 8. Cho tích phân
4
2
0
6tan
cos 3tan 1
x
Idx
xx
. Nếu đặt 3tan 1tx thì kết quả nào sau đây biểu diễn I
theo t?
Mã đề 166

2/6 - Mã đề 166
A.
22
1
421
3
Itdt
B.
22
1
41
3
Itdt
C.
22
1
41
3
Itdt
D.
22
1
421
3
Itdt
Câu 9. Gọi V là thể tích của khối tròn xoay có được khi quay hình phẳng giới hạn bởi các đường
11; 0; 1; 1yyxxkk
x
quay quanh trục Ox. Tìm k sao cho 15 ln16
4
V
.
A. 7k B. 8k C. 4k D. 16k
Câu 10. Trong không gian Oxyz cho véc tơ
2;1; 1 ; 1; 0; 2ab
.Tìm cosin của góc giữa hai véc tơ
trên.
A. 4
30
B. 2
30 C. 30
15
D. 215
15
Câu 11. Trong không gianOxyz , cho
1; 2; 6Mvà đường thẳng
22
:1
3
x
t
dy t
zt
. Tìm tọa độ điểm
M
đối
xứng với M qua đường thẳng
d.
A.
1; 2; 2 B.
1; 2; 2 C.
1; 2; 2 D.
1; 2; 2
Câu 12. Tìm nguyên hàm của hàm số
3
2
32
x
fx x x
.
A.
42
3ln 2 .ln2
4
x
x
x
C B.
3
3
12
3
x
xC
x
C.
432.ln2
4
x
xC
x
D.
432
4ln2
x
xC
x
Câu 13. Tìm nguyên hàm của hàm số
61
.
2
x
e
fx
A.
61 61
212
xx
ee
dx C
B.
61 61
3
2
x
x
edx e C
C.
61 61
3
2
x
x
edx e C
D. .
61 61
22
xx
ee
dx C
Câu 14. Biết tích phân
1
ln .
e
I
xxdx
2
.,
4
ae b ab
. Tính ab
A. 3 B. 4 C. 2 D. 1
Câu 15. Trong không gian Oxyz cho hai đường thẳng
12
:112
x
yz
d
và
1
:2
2
x
t
dyt
zt
. Tìm
phương trình mặt phẳng chứa đường thẳng
d và song song với đường thẳng
d.
A. 53 30xyz
B. 53 30xyz
C. 53 10xyz D. 5 3 1 0xyz
3/6 - Mã đề 166
Câu 16. Trong không gian Oxyz cho
1; 2; 3Mvà đường thẳng
1
:2
2
x
t
dyt
zt
. Tìm phương trình mặt
phẳng đi qua M và vuông góc với đường thẳng (d).
A. 220xyz
B. 230xyz C. 230xyz
D. 220xyz
Câu 17. Cho số phức z có phần ảo âm là nghiệm của phương trình 24200zz
trên tập số phức. Tìm
z.
A. 35
B. 5 C. 25
D. 52
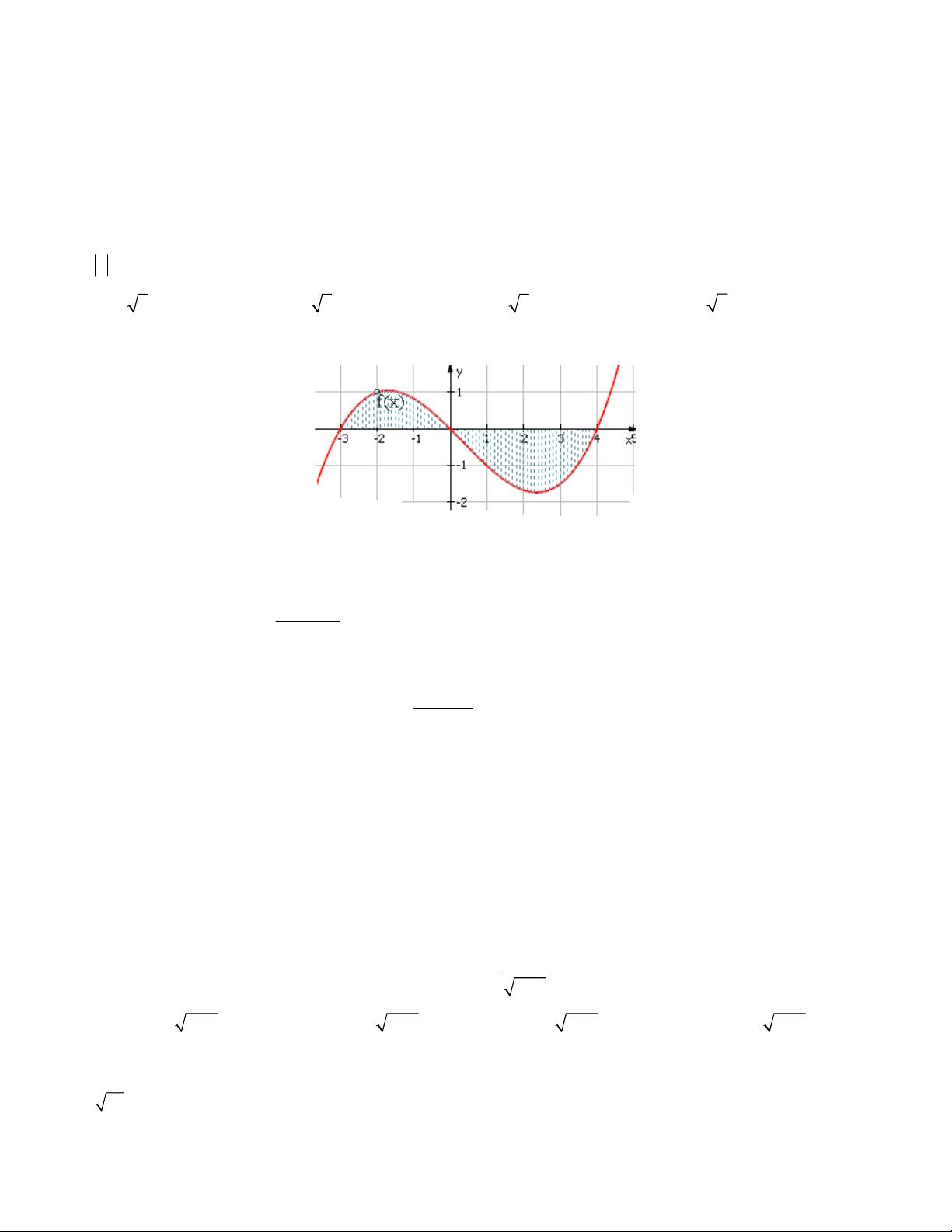
Câu 18. Cho đồ thị hàm số
yfx. Tìm diện tích hình phẳng (phần gạch sọc trong hình) .
A.
14
31
xx
f
xd f xd
B.
34
00
xx
f
xd f xd
C.
00
34
xx
f
xd f xd
D.
4
3
x
f
xd
Câu 19. Cho số phức
2019
1009
1
2
i
zi
. Tìm tổng phần thực và phần ảo của số phức z.
A. 2 B. 0 C. 1 D. 3
Câu 20. Tìm điểm biểu diễn của số phức
23 53
1
ii
zi
i
.
A.
9;5 B.
9; 5 C.
9;5 D.
9; 5
Câu 21. Véc tơ nào sau đây là véc tơ pháp tuyến của mặt phẳng
:3 2 7 0Pxz.
A.
3; 0; 2n
B.
3; 0; 2n
C.
3;1; 2n
D.
3;1; 2n
Câu 22. Biết
3
0
12fxdx
. Tính
1
0
3Ifxdx.
A. 4I B. 36I C. 6I D. 5I
Câu 23. Biết F(x) là một nguyên hàm của hàm số
1
1
fx x
và
33F. Tìm
Fx .
A.
11Fx x B.
211Fx x C.
11Fx x D.
211Fx x
Câu 24. Tìm tọa độ diểm M thuộc trục Ox và cách mặt phẳng
:2310xyz
một khoảng bằng
14 .
A.
0;13;0 ; 0; 15;0 B.
0;0;3 ; 0;0; 5 C.
13;0;0 ; 15;0;0 D.
13;0;0 ; 15;0;0

4/6 - Mã đề 166
Câu 25. Tính tích phân
2
0
sin 3
J
xdx
.
A. 2
3
J
B. 2
3
J C. 1
3
J D. 1
3
J
Câu 26. Biết
Fx là một nguyên hàm của hàm số
2
324fx x x
và
13F
. Trong các khẳng
định sau, tìm khẳng định đúng?
A.
32
41
F
xxx x
B.
2
625
F
xxx
C.
62
F
xx
D.
32
41Fx x x x
Câu 27. Tìm số phức liên hợp của số phức
2
12345zi i i .
A. 322i B. 322i C. 322i D. 322i
Câu 28. Tìm nguyên hàm của hàm số sau 2
23yx .
A.
23
2
23 3
x
dx x C
B.
23
3
23 3
2
x
dx x x C
C.
23
2
23 3
3
x
dx x x C
D.
23
3
23 3
2
x
dx x x C
Câu 29. Trong không gian Oxyz, cho hai đường thẳng
1
739
:12 1
xyz
d
và
2
311
:72 3
x
yz
d
. Tìm phương trình đường vuông góc chung của
1
dvà
2
d.
A. 739
214
xyz
B. 311
214
x
yz
C. 739
21 4
xyz
D. 311
214
x
yz
Câu 30. Tìm các giá trị thực của tham số m để phương trình sau
2
222 2
21 44594 0xyz m xmyzm m
là phương trình mặt cầu.
A. 41m B. 4m hoặc 1m
C. 1m D. 4m
Câu 31. Trong không gian Oxyz cho
1; 2; 3 ; 2; 0; 2MN. Tìm độ dài đoạn thẳng MN.
A. 13 B. 10 C. 6 D. 7
Câu 32. Tính tích phân
1
0
1
21
Idx
x
.
A. 1ln 3
2
I B. ln 3I C. ln 2I D. 1ln 2
2
I
Câu 33. Cho hai số phức 12
12; 3zizi .Tìm 12
zz
A. 15 B. 17 C. 5 D. 17
Câu 34. Tìm tọa độ véc tơ chỉ phương của đường thẳng
12
:321
xy z
.
5/6 - Mã đề 166
A.
6; 4; 2 B.
3; 4;1 C.
3; 4;1 D.
3; 4; 1
Câu 35. Viết phương trình mặt cầu có tâm
0;3; 2Ivà đi qua điểm
2;1; 3A.
A.
22
2
:329Sx y z B.
22
2
:323Sx y z
C.
22
2
:323Sx y z D.
22
2
:329Sx y z
Câu 36. Tìm mô đun của số phức
232wii .
A. 63 B. 66 C. 65 D. 67
Câu 37. Trong không gian Oxyz, cho điểm
1; 0; 2Avà đường thẳng
11
:112
x
yz
d
. Tìm phương trình
đường thẳng đi qua
A
, vuông góc và cắt d.
A. 12
221
xyz
B. 12
131
xyz
C. 12
111
xyz
D. 12
11 1
xyz
Câu 38. Tính tích phân
1
2
0
1
x
K
xe dx
A. 21Ke
B. 2
11
2
Ke
C. 2
21Ke
D. 2
21Ke
Câu 39. Tìm phương trình đường thẳng đi qua
1; 3; 2Mvà vuông góc với mặt phẳng
:3450xyz
.
A.
12
33
28
x
t
yt
zt
B.
1
33
24
x
t
yt
zt
C.
1
33
24
x
t
yt
zt
D.
12
33
24
x
t
yt
zt
Câu 40. Cho 2
x
Ixedx, đặt 2
tx. Hãy viết I theo t và dt .
A. t
Iedt B. t
Itedt C. 1
2
t
Iedt D. 2t
Iedt
Câu 41. Tìm phương trình đường thẳng đi qua
1; 0; 4Avà có véc tơ chỉ phương
2;3; 1u
.
A.
12
3
2
x
t
yt
zt
B.
11
3
4
x
t
yt
zt
C.
12
3
4
x
t
yt
zt
D.
11
3
4
x
t
yt
zt
Câu 42. Tìm nghiệm của phương trình : 2
2430xx
trên tập số phức.
A. 12;12ii
B. 22
1;1
22
ii C. 22
1;1
22
ii
D. 12;12ii
Câu 43. Tìm tổng sau : 246 2018
1 ....Siii i .
A. 2S B. 0S C. 1S D. 1S
Câu 44. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2
432yx xvà đồ thị hàm số 52.yx












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



