MÔN: TOÁN HỌC 9
Ngày kiểm tra: 13/12/2017
(Thời gian làm bài: 90 phút)
Câu 1: (2,0 điểm) Cho biểu thức: P =
1
)12(2
:
11
x
xx
xx
xx
xx
xx
a. Rút gọn P.
b. Tìm x để P< 0.
c. Tìm x nguyên để P có giá trị nguyên.
Câu 2: (1,5 điểm)
Cho hàm số bậc nhất: y = (m+1)x - 2m (1)
a. Tìm m để hàm số trên là hàm số bậc nhất.
b. Tìm m để đồ thị hàm số (1) song song với đồ thị hàm số y = 3x +6.
c. Chứng minh rằng đồ thị hàm số (1) luôn đi qua 1 điểm cố định với mọi m.
Câu 3: (2,0 điểm)
Một cây xanh có bóng trên mặt đất dài bằng 2/3 chiều cao của nó. Tính
góc tạo bởi cây đó với các tia nắng mặt trời.
Câu 4: ( 3,5 điểm)
Cho nửa đường tròn (O) đường kính AB. Vẽ các tiếp tuyến Ax, By về nửa
mặt phẳng bờ AB chứa nửa đường tròn. Trên Ax và By theo thứ tự lấy M và N
sao cho góc MON bằng 900. Gọi I là trung điểm của MN. Chứng minh rằng:
a. AB là tiếp tuyến của đường tròn (I;IO)
b. MO là tia phân giác của góc AMN
c. MN là tiếp tuyến của đường tròn đường kính AB.
Câu 5: (1,0 điểm) Rút gọn các biểu thức sau:
A =
15 216 33 12 6
B = 1 1 1 1
...
1 2 2 3 3 4 2016 2017
........................................Hết...................................
PHÒNG GD & ĐT ĐÔNG TRIỀU
TRƯỜNG THCS KIM SƠN
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC 2017-2018
Câu Nội dung Điểm
Câu 1
(2,0 đ)
a. (1điểm) ĐKXĐ: 0 1
x
.
P =
2
2
23
3
3
3
1
)1.(2
:
)1(
1
1(
1
x
x
xx
x
xx
x
P =
)1)(1(
)1(2
:
)1(
)1)(1(
)1(
)1)(1( 2
xx
x
xx
xxx
xx
xxx
P =
1
)1(2
:
11
x
x
x
xx
x
xx
P =
)1(2
1
.
11
x
x
x
xxxx
P =
)1(2
1
.
2
x
x
x
x
P = 1
1
x
x
b. (0.75điểm) Để P < 0 thì: 1
1
x
x
< 0
01x
1x
x<1
Kết hợp ĐKXĐ ta có: Để
P<0 thì 0<x<1.
c.(0,25điểm) Ta có: P = 1
1
x
x= 1
2
1
x Để P
Z thì 2
1x 2;11 x
0,25
0,5
0,25
0,5
0,25
0,25
PHÒNG GD & ĐT ĐÔNG TRIỀU
TRƯỜNG THCS KIM SƠN
ĐÁP ÁN-BIỂU ĐIỂM CHẤM KIỂM TRA
HỌC KỲ I NĂM HỌC 2017 – 2018
MÔN: TOÁN 9
Ta có bảng sau:
1x -2 -1 1
x Không có giá trị
của x
0 4
Dựa vào bảng trên và ĐKXĐ ta có: x = 4; 9
Vậy để P
Z thì x = 4 hoặc x = 9
Câu 2
( 1,5 đ)
a. (0,5điểm) Để hàm số trên là hàm số bậc nhất thì: m + 1
0
m
-1
b. (0,5điểm) Để đồ thị hàm số (1) song song với đồ thị hàm
số y = 3x+6 thì:
62
31
m
m
3
2
m
m
m= 2. Vậy m = 2 thì đồ thị hàm số (1) song song với đồ
thị hàm số y= 3x+6.
c.(0,5điểm) Gọi M( 00 ;yx ) là điểm cố định mà đồ thị (1) luôn
đi qua. Khi đó, phương trình:
y0 = (m+1)x 0 - 2m luôn có nghiệm với mọ
i m
phương trình: mx 0-2m + x0- y 0= 0 luôn có nghiệm với
mọi m
phương trình: m(x 0-2) + (x0- y 0) = 0 luôn có nghiệm với
mọi m
0
02
00
0
yx
x
2
2
0
0
y
x.
Vậy đồ thị hàm số (1) luôn đi qua điểm M(2;2) cố đị
nh.
0,5
0,5
0,5
Câu 3
( 2,0 đ)
Gọi cây đó cao một đoạn AB, bóng của cây trên mặt đất là
AC, khi đó góc tạo bởi cây với các tia nắng mặt trời là góc
ABC = α .
Vì cây vuông góc với mặt đất nên, ∆ABC vuông tại A.
AD tỉ số lượng giác trong tam giác vuông, ta có:
tanB = AC: AB= 2/3 AB : AB = 2/3
B ≈ 340
Vậy góc tạo bởi các tia nắng mặt trời với cây xanh
là gần bằng 340
1,0
1,0
A
C
B
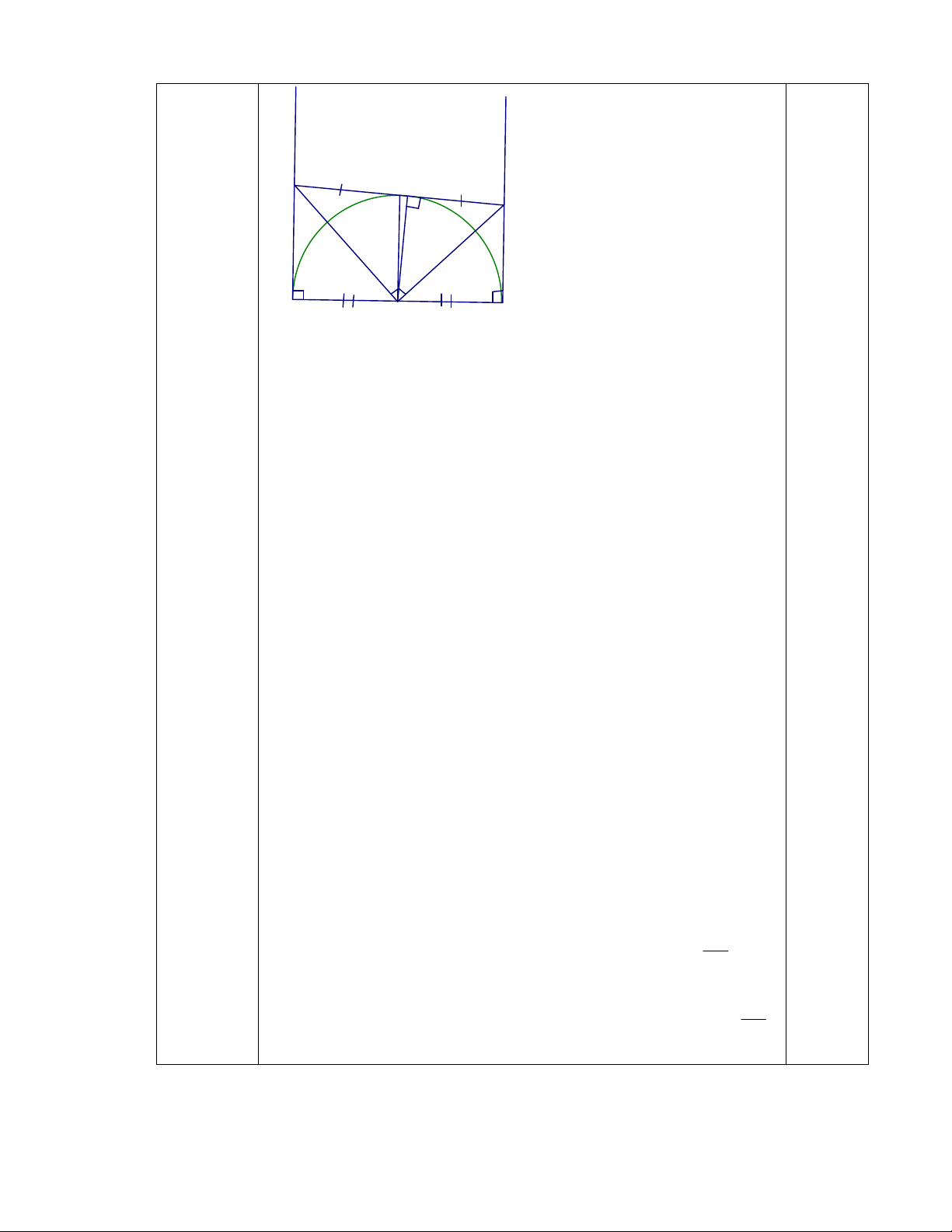
Câu 4
(3,5 đ)
Chứng minh
a. (1,5điểm)
Tứ giác ABNM có AM//BN (vì cùng vuông góc với AB) =>
Tứ giác ABNM là hình thang.
Hình thang ABNM có: OA= OB; IM=IN nên IO là đường
trung bình của hình thang ABNM.
Do đó: IO//AM//BN. Mặt khác: AM
AB suy ra IO
AB tại
O.
Vậy AB là tiếp tuyến của đường tròn (I;IO)
b.(1,0 điểm)
Ta có: IO//AM =>
AMO
=
MOI
( 1)
Lại có: I là trung điểm của MN và MON vuông tại O
(gt) ;
nên MIO cân tại I.
Hay
OMN
=
MOI
(2)
Từ (1) và (2) suy ra:
AMO
=
OMN
. Vây MO là tia phân giác
của AMN.
c. (0,5điểm)Kẻ OH
MN (H
MN). (3)
Xét OAM và OHM có:
OAM
=
OHM
= 900
AMO
=
OMN
( chứng minh trên)
MO là cạnh chung
Suy ra: OAM = OHM (cạnh huyền- góc nhọ
n)
Do đó: OH = OA => OH là bán kính đường tròn (O;
2
AB ).
(4)
Từ (3) và (4) suy ra: MN là tiếp tuyến của đường tròn (O;
2
AB
).
0,5
0,5
0,5
0,5
0,5
0,5
0,5
I
y
x
H
M
N
B
O
A
Câu 5
( 1,0 đ)
A=
15 216 33 12 6
=…=
2 2
(3 6) (2 6 3)
=
3 6 2 6 3
=
6
B = 1 1 1 1
...
1 2 2 3 3 4 2016 2017
=
2 1 3 2 4 3 ... 2017 2016
=…=
2017 1
0.25
0.25
0.25
0.25
Tổng 10