TRƯỜNG THCS TÂN BÌNH NH: 21 - 22 TOÁN 9
1
ĐỀ THAM KHẢO ÔN KIỂM TRA HKI
TOÁN 9
NĂM HỌC 2021 - 2022
ĐỀ 1:
Bài 1 : Thực hiện phép tính (1điểm)
Bài 2 : Giải phương trình (1,5 điểm)
Bài 3 : (1,5 điểm)
Cho hàm số y = x +2 có đồ thị (𝐷1) và hàm số y = -2x-1 có đồ thị (𝐷2)
a/ Vẽ (𝐷1) 𝑣à (𝐷2) 𝑡𝑟ê𝑛 𝑐ù𝑛𝑔 ℎệ 𝑡𝑟ụ𝑐 𝑡ọ𝑎 độ
b/ Tìm tọa độ giao điểm của (𝐷1) 𝑣à (𝐷2)
Bài 4 : (1 điểm)
Một cửa hàng thời trang nhập về 100 đôi giày với giá vốn là 300000 đồng / 1 đôi.
Đợt 1 cửa hàng bán hết 80 đôi. Nhân dịp khuyến mãi, để bán hết phần còn lại, cửa
hàng đã giảm 30% so với giá niêm yết ở đợt một. Biết rằng khi bán hết số giày của
đợt nhập hàng này thì cửa hàng lãi 12300000 đồng.
a)Tính tổng số tiền cửa hàng thu về khi bán hết 100 đôi giày.
b) Hỏi vào dịp khuyến mãi cửa hàng đó bán một đôi giày bao nhiêu tiền?
Bài 5: (1 điểm)
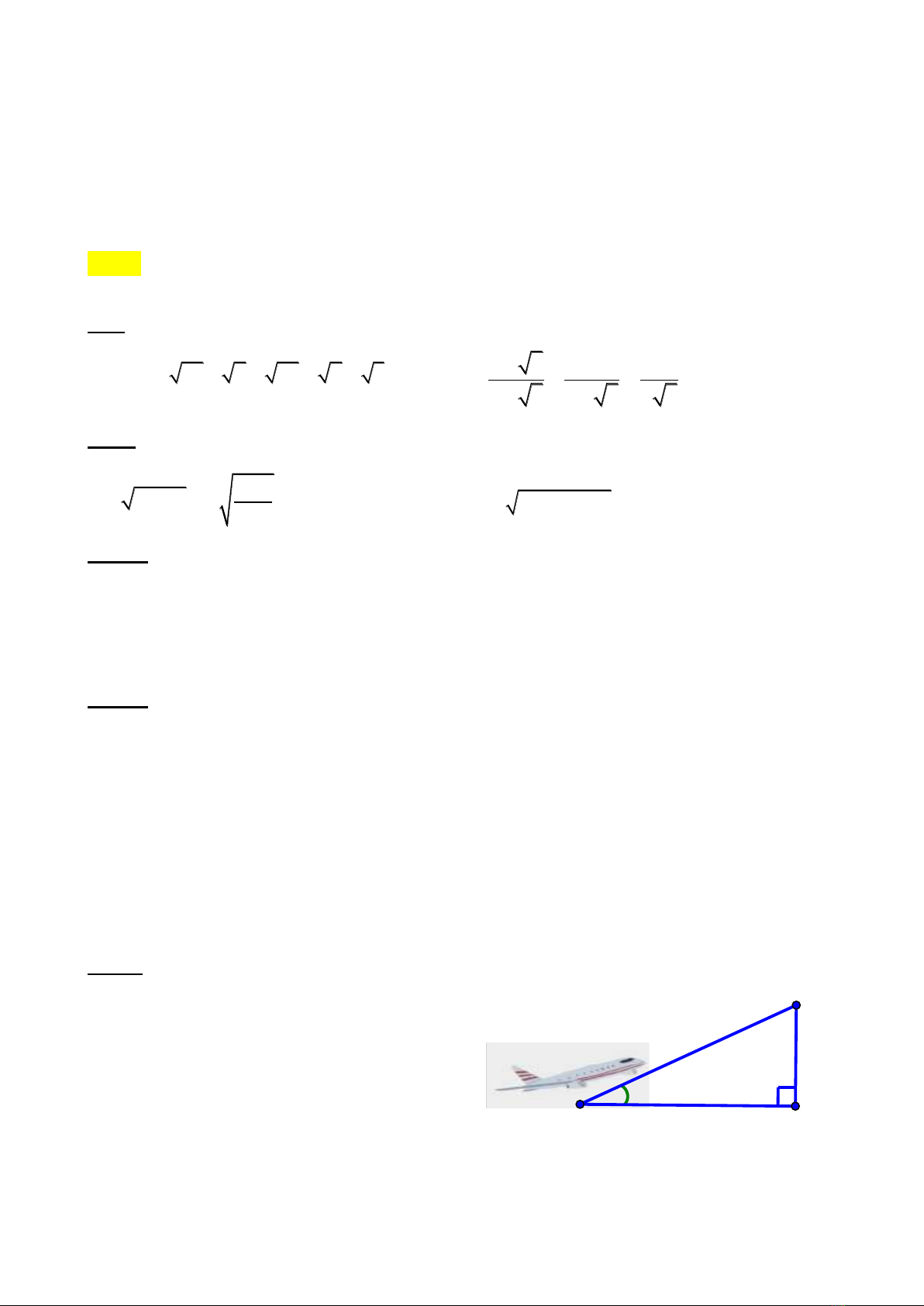
Một chiếc máy bay bay lên với vận tốc
trung bình 300km/h. Đường bay lên tạo với
phương nằm ngang một góc 250. Hỏi sau 3
phút máy bay bay lên đạt được độ cao là
bao nhiêu mét (làm tròn đến hàng đơn vị).
( )( )
) 75 2 48 2 3a− − +
3 5 3 45
)3 5 3 5 4 5
b−−+
+−
1
) 9 9 4 5
4
x
ax +
+ = +
2
) 9 6 1 2b x x− + =
K
Q
I
25
TRƯỜNG THCS TÂN BÌNH NH: 21 - 22 TOÁN 9
2
Bài 6: (1 điểm)
Một cái hồ khi còn chứa 3 m3 nước thì van tự động mở một vòi nước chảy vào hồ với
vận tốc 4 m3/giờ. Gọi y (m3) là thể tích nước trong hồ sau x (giờ) vòi nước chảy vào
hồ.
a) Em hãy viết công thức hàm số bậc nhất tính y theo x.
b) Biết dung tích của hồ nước là 21 m3. Hỏi vòi chảy trong bao lâu thì đầy hồ nước ?
Bài 7: (3điểm)
Cho ABC vuông tại A có đường cao AH.
a/ Biết AB = 30cm, BC = 50cm. Tính AH và HC
b/ Vẽ đường tròn (O,R) đường kính AC. Chứng minh AB là tiếp tuyến của đường
tròn (O).
c/ Đường thẳng kẻ từ O vuông góc với HC cắt tiếp tuyến tại C của đường tròn (O) ở
điểm K. Chứng minh:
·
OK.sin BAH R=
ĐỀ 2:
Bài 1: (1,5 điểm) Thực hiện phép tính (thu gọn):
a)
10814722748 −+−
b)
25
2050
310
1
+
+
−
−
Bài 2: (1 điểm) Giải phương trình sau: √4𝑥2−4𝑥+1=7
Bài 3: (1,5 điểm) Cho hàm số y = x + 1 (d1) và hàm số y = 4 – 2x (d2)
a) Vẽ (d1) trên mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm A của (d1) và (d2) bằng phép toán
Bài 4: (1 điểm) Giá bán một cái tủ giảm giá hai lần, mỗi lần giảm giá 20% so với giá đang
bán, sau khi giảm giá hai lần đó thì giá còn lại là 12 800 000 đồng. Vậy giá bán ban đầu của
cái tủ là bao nhiêu?
TRƯỜNG THCS TÂN BÌNH NH: 21 - 22 TOÁN 9
3
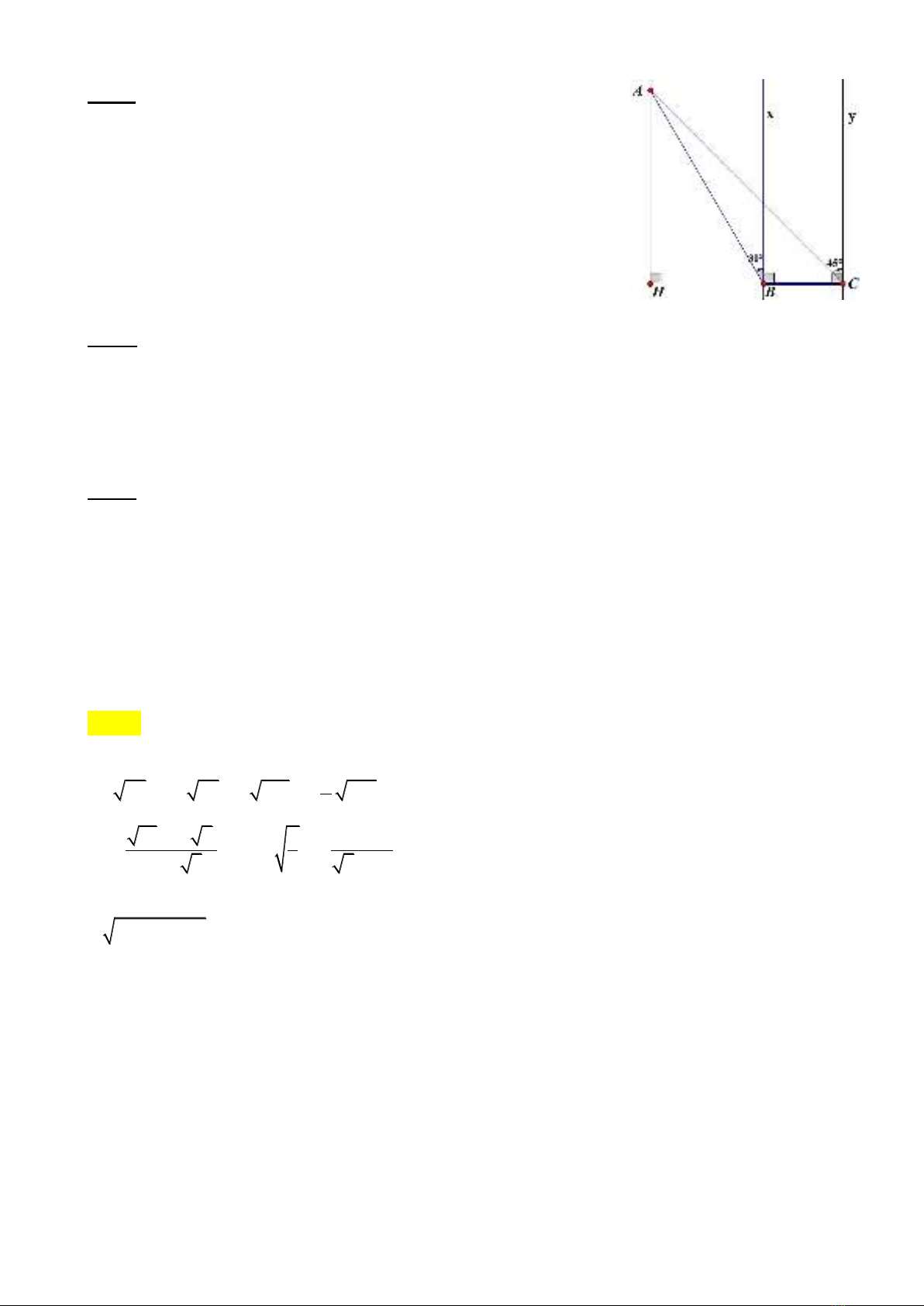
Bài 5: (1 điểm) Một chiếc flycam (thiết bị bay điều khiển từ
xa dùng để chụp ảnh và quay phim từ trên không) đang ở vị
trí A cách chiếc cầu BC (theo phương thẳng đứng) một
khoảng AH = 120m. Biết góc tạo bởi AB, AC với các phương
vuông góc với mặt cầu tại B, C thứ tự là
·
0
ABx 30=
;
·
0
ACy 45=
. Tính chiều dài BC của cây cầu. (Làm tròn kết quả
đến chữ số thập phân thứ hai.)
Bài 6: (1 điểm) Một cửa hàng nhập về nhãn hàng máy tính xách tay với giá vốn là
4500000 đồng. Cửa hàng dự định công bố giá niêm yết (giá bán ra) là 6000000 đồng.
a) Nếu bán với giá niêm yết trên thì cửa hàng lãi bao nhiêu phần trăm so với giá vốn?
b) Để có lãi ít nhất 5% thì cửa hàng có thể giảm giá nhiều nhất bao nhiêu phần trăm?
Bài 7: (3 điểm) Từ điểm A bên ngoài đường tròn (O), vẽ hai tiếp tuyến AB, AC với
đường tròn (O) (B, C là 2 tiếp điểm). Vẽ đường kính BD. Gọi H là giao điểm của AO
và BC.
a) Chứng minh AO ⊥ BC tại H và CD // OA.
b) Vẽ CM ⊥ BD (M BD). Chứng minh DM . DB = 4OH2.
c) Gọi E (O) sao cho BE = BH. Gọi I trung điểm BH. Vẽ IK ⊥ BD (K BD).
Chứng minh BK . BD = BI . BC và I, K , E thẳng hàng.
ĐỀ 3:
Bài 1: Thực hiện phép tính (thu gọn): (1,5 điểm)
1
1) 20 4 45 180 320
4
+ − −
2)
15 2 5 1 4
10 5
2 3 5 3
−++
−−
Bài 2: Giải phương trình: (1 điểm)
2
2 x 4x 4 6 0− + − =
Bài 3:(1,5 điểm)
Cho hàm số y = 2x − 3 có đồ thị là (D1) và hàm số
3yx= − −
có đồ thị là (D2)
1) Vẽ (D1) và (D2) trên mặt phẳng tọa độ
2) Tìm tọa độ giao điểm A của (D1) và (D2) bằng phép toán
Bài 4: (1 điểm) Lực F của gió khi thổi vuông góc vào cánh buồm tỉ lệ thuận với bình
phương vận tốc v của gió, tức là
2
F av=
(a là hằng số). Biết rằng khi vận tốc của gió
là 2m/s thì lực tác động lên cánh thuyền buồm của một con thuyền bằng 120N
TRƯỜNG THCS TÂN BÌNH NH: 21 - 22 TOÁN 9
4
(Niu-tơn). Tính hằng số a rồi cho biết con thuyền có thể đi được trong gió bão với
vận tốc 90km/h hay không? Biết rằng cánh buồm chỉ có thể chịu được một áp lực tối
đa là 12000 N.
Bài 5: (1 điểm) Đầu tháng 11 vừa qua, các trung tâm thương mại bắt đầu hoạt động
trở lại sau đợt nghỉ dịch Covid kéo dài 5 tháng. Để kích cầu mua sắm, phần lớn các
trung tâm thương mại đều giảm giá rất nhiều mặt hàng. Mẹ bạn Tùng có dẫn Tùng
đến một trung tâm thương mại để mua một đôi giầy thể thao. Biết một đôi giầy thể
thao đang đang được khuyến mãi giảm giá 40%, mẹ bạn Tùng có thẻ khách hàng thân
thiết của trung tâm thương mại nên được giảm thêm 5% trên giá đã giảm, mẹ bạn
Tùng chỉ phải trả 1026000 đồng cho đôi giầy thể thao? Hỏi giá
ban đầu của một đôi giầy thể thao là bao nhiêu?
Bài 6: (1 điểm) Một khúc sông rộng khoảng 157m. Một con tàu
mất 5 phút để đi từ vị trí B (bờ bên này) đến vị trí C (bờ bên kia).
Tàu đi với vận tốc 2km/h và bị dòng nước đẩy lệch đi một góc 𝛼
như hình vẽ. Tính góc 𝛼 (kết quả làm tròn đến độ).
Bài 7: (3 điểm) Cho đường tròn (O) có đường kính AB = 2R và dây cung AC = R.
a) Chứng minh ABC vuông và tính độ dài cạnh BC theo R.
b) Trên tia OC lấy D sao cho C là trung điểm của OD. Chứng minh AD là tiếp tuyến
của (O).
c) Vẽ tiếp tuyến DE của (O) (E là tiếp điểm). Chứng minh ADE đều.
d) Tiếp tuyến tại B của (O) cắt đường thẳng AE tại M, gọi K là giao điểm của BD và
OM. Tính bán kính của đường tròn ngoại tiếp OKB theo R.
ĐỀ 4:
Bài 1:(3 điểm) Tính:
a)
1
2 12 . 75 27
5
- + -
b)
( )
2
52 16 3 4 3 7- + -
c)
27 3 2 2 10
3 2 5 2 5
-+-
--
Bài 2:(1 điểm) Giải phương trình:
a)
2
x 6x 9 x 2- + = -
b)
8
9
2
63216 +
−
=− x
x
Bài 3: (1,5 điểm) Cho hàm số y = x + 2 có đồ thị là (d1) và hàm số y = – 2x – 1 có
đồ thị là (d2).
TRƯỜNG THCS TÂN BÌNH NH: 21 - 22 TOÁN 9
5
a) Vẽ (d1) và (d2) trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ giao điểm của (d1) và (d2).
Bài 4: Lớp 9A có 46 học sinh. Tổng kết đợt báo điểm tháng 11 của năm học 2018 –
2019 học lực của lớp 9A gồm hai loại giỏi và khá. Biết rằng ba phần tư số học sinh giỏi
bằng hai phần năm số học sinh khá. Hỏi lớp 9A có bao nhiêu học sinh giỏi, bao nhiêu
học sinh khá?
Bài 5: (1 điểm) Công ty A đã sản xuất ra những chiếc máy nước nóng với số vốn ban
đầu là 800 triệu đồng. Chi phí để sản xuất ra một chiếc máy nước nóng là 2,5 triệu
đồng. Giá bán ra mỗi chiếc máy nước nóng là 3 triệu đồng.
a) Viết hàm số y (triệu đồng) biểu diễn tổng số tiền công ty đã đầu tư (gồm vốn ban
đầu và chi phí sản xuất) để sản xuất ra x máy nước nóng.
b) Công ty A cần bán ít nhất bao nhiêu máy nước nóng mới có thể thu hồi vốn ban đầu?
Giải thích.
Bài 6: (1 điểm)
Bài 7: (2,5 điểm) Cho nửa đường tròn tâm O, bán kính R, đường kính AB. D là điểm
thuộc nửa đường tròn sao cho DA > DB. Gọi DH là đường cao của tam giác DAB. Biết
DH = 6cm, HB = 4,5cm.
a) Chứng minh tam giác DAB vuông và tính độ dài DB, DA.
b. Gọi G là trung điểm của BD. Tia OG cắt tiếp tuyến tại B của đường tròn (O; R) tại
F. Chứng minh FD là tiếp tuyến của đường tròn (O; R) và góc DAF bằng góc BAG.
c. Đoạn AF cắt DO, DH thứ tự tại I, P. Chứng minh diện tích của tứ giác BPIO và diện
tích của tam giác DIA bằng nhau.
ĐỀ 5:
Bài 1 (1,5 điểm) :Tính:
a)
6410545242/ ++−a
b)
( )
2
18 12 4
+ 3 3 12
6 2 3 1
−+−
−+
Bài 2 (1điểm): Giải phương trình:
x4
16x 64 12 2 4x 16 6
4
−
− − + − =
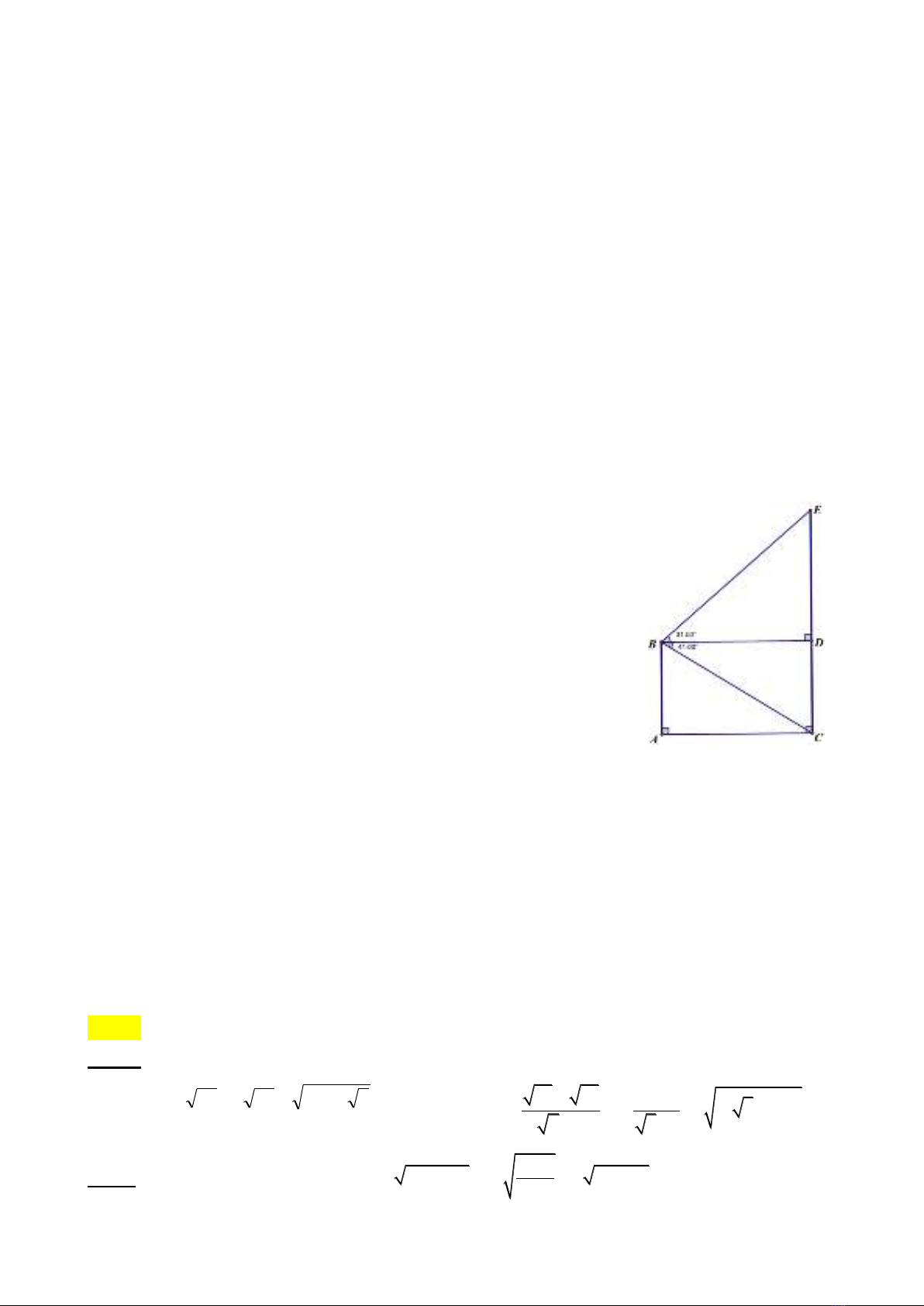
Một kỹ sư đứng ở vị trí B (nóc của tòa nhà AB) và
dùng thiết bị quan sát thấy góc nhìn (so với
phương ngang) từ B đến đỉnh E và chân C của cột
phát sóng CE lần lượt là 31,50 và 410. Biết chiều
cao của tòa nhà là 50 mét, tính chiều cao CE của
cột phát sóng (kết quả làm tròn đến chữ số thập
phân thứ hai).