
——————————–Bộ đề ôn thi học kỳ 2, năm học 2020-2021——————————–
SỞ GIÁO DỤC VÀ ĐÀO TẠO:−−−−−−−−−−−−−−−
TRƯỜNG:−−−−−−−−−−−−−−−−
ĐỀ ÔN SỐ 1
ĐỀ KIỂM TRA HK 2, NĂM HỌC 2020-2021
MÔN TOÁN-THPT
Thời gian làm bài 90 phút, không tính thời gian giao đề
Câu 1. Trong không gian Oxyz, phương trình đường thẳng đi qua hai điểm M(2; −1; 1) và N(0; 1; 3) là
A.(x= 2 + t
y=−1−t
z= 1 −t
.B.(x= 2 + t
y= 1 −t
z=−1−t
.C.(x= 2 + t
y=−1
z= 1 + 2t
.D.®x= 2
y=−1 + t
z= 1 + 3t
.
Câu 2. Các nghiệm phương trình của z2+ 4 = 0 là
A.z= 2ivà z=−2i.B.z=ivà z=−i.C.z= 4ivà z=−4i.D.z= 2 và z=−2.
Câu 3. Giá trị của tích phân bằng Z1
xdxbằng
A. 1. B.−1.C.1
e.D.e.
Câu 4. Cho số phức z=x+yi(x, y ∈R)thỏa mãn z+ 2z= 2 −4i. Giá trị của 3x+ybằng
A. 10. B. 7. C. 5. D. 6.
Câu 5. Phương trình bậc hai nhận hai số phức 2 + 3ivà 2−3ilàm nghiệm là
A.−z2+ 4z−6 = 0.B.z2+ 4z+ 13 = 0.C.2z2+ 8z+ 9 = 0.D.z2−4z+ 13 = 0.
Câu 6. Nếu đặt u= 2x+ 1 thì
1
Z
0
(2x+ 1)4dxbằng
A.
1
Z
0
u4du.B.1
2
3
Z
1
u4du.C.
3
Z
1
u4du.D.1
2
1
Z
0
u4du.
Câu 7. Trong không gian với hệ tọa độ Oxyz , cho hai điểm M(3; 1; 4), N(0 : 2; −1). Tọa độ trọng tâm của
tam giác MON là
A.(−3; 1; −5).B.(1; 1; 1).C.(−1; −1; −1).D.(3; 3; 3).
Câu 8. Giá trị thực của xvà ysao cho x2−1 + yi =−1 + 2ilà
A.x=√2và y=−2.B.x=−√2và y= 2.C.x=√2và y= 2.D.x= 0 và y= 2.
Câu 9. Biết
2
Z
0
(3x−1) e
x
2dx=a+be với a, b là các số nguyên. Giá trị a+bbằng
A.10.B.16.C.6.D.12.
Câu 10. Họ tất cả các nguyên hàm của hàm số f(x) = x3là
A.x4
4+C.B.3x2+C.C.x4+C.D.x3
3+C.
Câu 11. Trong không gian Oxyz, khoảng cách giữa hai mặt phẳng (P) : x+ 2y+ 2z+ 11 = 0 và (Q) :
x+ 2y+ 2z+ 2 = 0 bằng
A.9.B.6.C.3.D.1.
Câu 12. Cho hình phẳng Dgiới hạn bởi đồ thị hàm số y=√6xvà các đường thẳng y= 0, x = 1, x = 2. Thể
tích khối tròn xoay tạo thành khi quay Dquanh trục hoành bằng
A.π
1
Z
0
6x2dx.B.π
2
Z
1
√6xdx.C.π
2
Z
1
6x2dx.D.π
2
Z
0
6x2dx.
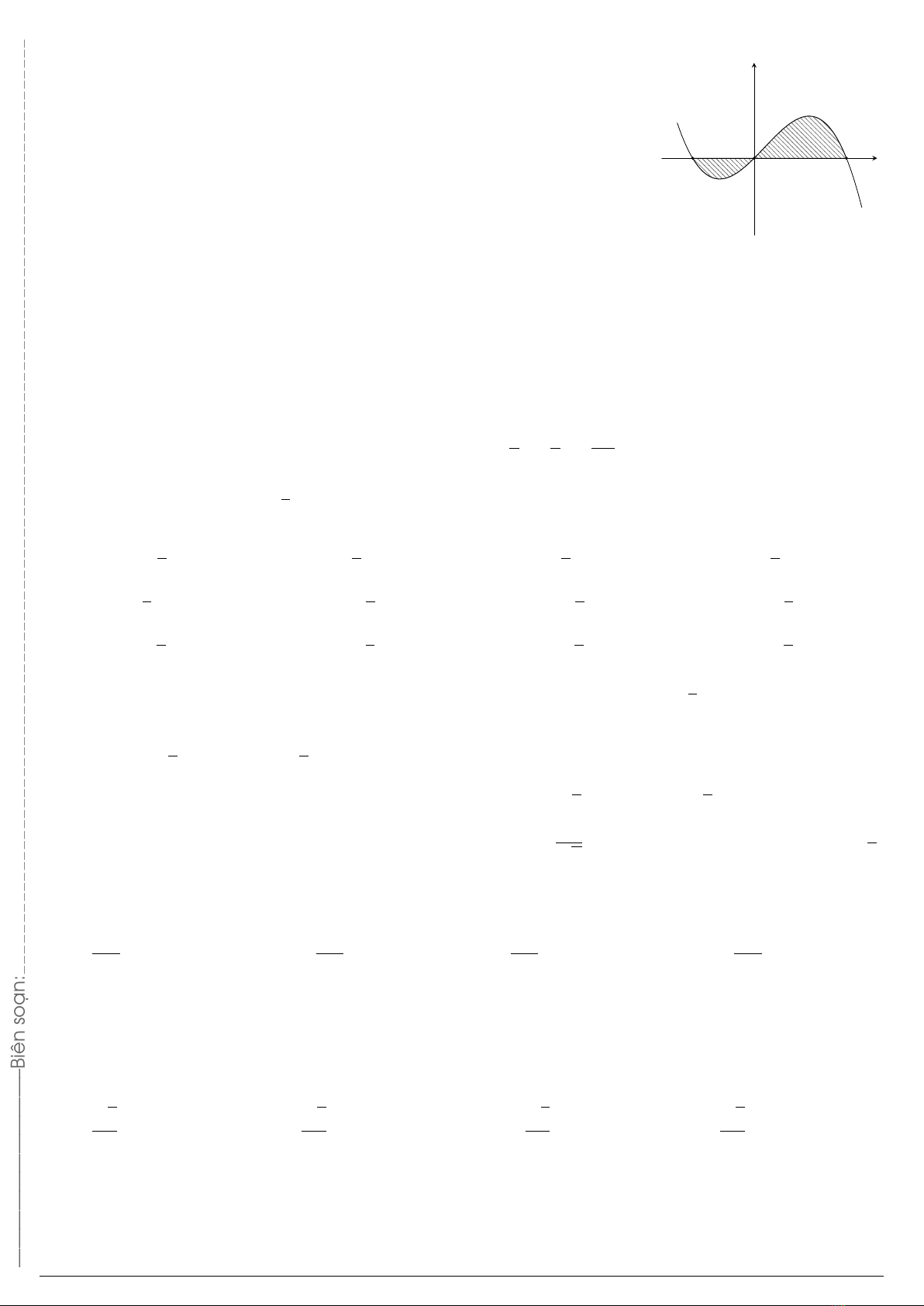
Câu 13. Cho hàm số y=f(x)có đồ thị như hình vẽ. Diện tích phần tô đậm bằng
x
y
O
1
2
−2
Bộ đề ôn thi học kỳ 2-Toán 12 Trang 1

——————————–Biên soạn:−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
A.
1
Z
−2|f(x)|dx.B.
1
Z
0|f(x)|dx.C.
2
Z
0|f(x)|dx.D.
0
Z
−2|f(x)|dx.
Câu 14. Trong không gian Oxyz, phương trình mặt phẳng đi qua điểm A(−3; 4; −2) và nhận vectơ #»
n=
(−2; 3; −4) làm vectơ pháp tuyến là
A.2x−3y+ 4z+ 29 = 0.B.2x−3y+ 4z+ 26 = 0.
C.−3x+ 4y−2z−26 = 0.D.−2x+3y−4z+ 29 = 0.
Câu 15. Trong không gian Oxyz, phương trình đường thẳng đi qua điểm M(1; 1; −2) và vuông góc với mặt
phẳng (P) : x−y−z−1 = 0 là:
A.x+ 1
1=y+ 1
−1=z−2
−1.B.x−1
1=y−1
1=x+ 2
−2.
C.x−1
1=y−1
−1=x+ 2
−1.D.x−1
1=y+ 1
1=z+ 1
−2.
Câu 16. Diện tích hình phẳng giới hạn bởi đồ thị hàm số y= exvà các đường thẳng y= 0;x= 0;x= 2
bằng
A.πZ2
0
exdx.B.Z2
0
e2xdx.C.πZ2
0
e2xdx.D.Z2
0
exdx.
Câu 17. Cho hình phẳng Dgiới hạn bởi đồ thị hàm số y= 2x−x2và trục Ox. Thể tích khối tròn xoay được
tạo thành khi quay Dquanh trục Ox bằng
A.16π
15 .B.4π
3.C.256π
15 .D.64π
15 .
Câu 18. Trong mặt phẳng Oxy, biết rằng tập hợp các điểm biểu diễn số phức zthỏa mãn |z−2 + 4i|= 5 là
một đường tròn. Tọa độ tâm của đường tròn đó là
A.(−1; 2).B.(−2; 4).C.(1; −2).D.(2; −4).
Câu 19. Gọi z1, z2là hai nghiệm của phương trình z2−2z+ 5 = 0. Giá trị của z2
1+z2
2+z1z2bằng:
A.−1.B.1.C.9.D.−9.
Câu 20. Cho số phức z=−5 + 2i. Phần thực và phần ảo của số phức zlần lượt là
A.−5và 2.B.−5và −2.C. 5 và −2.D. 5 và 2.
Câu 21. Môđun của số phức z= 4 −3ibằng
A.7.B.√7.C.5.D.1.
Câu 22. Trong không gian Oxyz, cho #»
a= (−3; 1; 2) và #»
b= (0; −4; 5). Giá trị của #»
a .
#»
bbằng
A.6.B.3.C.10.D.−14.
Câu 23. Trong không gian Oxyz, tọa độ tâm mặt cầu (S) : x2+y2+z2−2x+ 2y−4 = 0 là
A.(−2; 2; 0).B.(−1; 1; 0).C.(1; −1; 0).D.(1; −1; 2).
Câu 24. Gọi a, b lần lượt là phần thực và phần ảo của số phức z=−3 + 2i. Giá trị của a−bbằng
A.1.B.5.C.−5.D.−1.
Câu 25. Cho hai số phức z1= 5 −6ivà z2= 2 + 3i. Số phức 3z1−4z2bằng
A.26 −15i.B.23 −6i.C.−14 + 33i.D.7−30i.
Câu 26. Trong không gian Oxyz, cho điểm A(2; 4; 1) và mặt phẳng (P) : x−3y+ 2z−5 = 0. Phương trình
của mặt phẳng đi qua điểm Avà song song với mặt phẳng (P)là
A.2x+ 4y+z−8 = 0.B.x−3y+ 2z−8 = 0.C.2x+ 4y+z+ 8 = 0.D.x−3y+ 2z+ 8 = 0.
Câu 27. Trong không gian Oxyz, cho các điểm A(−1; 1; 3), B(2; 1; 0), C(4; −1; 5). Một véc tơ pháp tuyến của
mặt phẳng (ABC)có tọa độ là
A.(−2; 7; −2).B.(16; 1; −6).C.(2; 7; 2).D.(16; −1; 6).
Câu 28. Diện tích hình phẳng giới hạn bởiđồ thị các hàm số y=x2, y =xvà các đường thẳng x= 0, x = 1
bằng
A.
1
Z
0x2+xdx.B.
0
Z
−1x2+xdx.C.
1
Z
0x2−xdx.D.
0
Z
−1x2−xdx.
Bộ đề ôn thi học kỳ 2-Toán 12 Trang 2

——————————–Bộ đề ôn thi học kỳ 2, năm học 2020-2021——————————–
Câu 29. Cho hàm số f(x)và g(x)liên tục trên đoạn [1; 7] sao cho
7
Z
1
f(x)dx= 2 và
7
Z
1
g(x)dx=−3. Giá trị
của
7
Z
1
[f(x)−g(x)] dxbằng
A. 6. B. 5. C. -1. D. -5.
Câu 30. Trong mặt phẳng Oxy, điểm biểu diễn của z= 2 −icó tọa độ là
A.(2; −1).B.(−2; 1).C.(2; 1).D.(−2; −1).
Câu 31. Trong không gian Oxyz, cho hai vectơ #»
a= (2; m;n)và #»
b= (6; −3; 4) với m,nlà các tham số thực.
Giá trị của m,nsao cho hai vectơ #»
avà #»
bcùng phương là
A.m=−1và n=4
3.B.m=−1và n=3
4.C.m= 1 và n=4
3.D.m=−3và n= 4.
Câu 32. Họ tất cả các nguyên hàm của hàm số f(x) = x(x2+ 1)9là
A.1
20(x2+ 1)10 +C.B.1
10(x2+ 1)10 +C.C.(x2+ 1)10 +C.D.1
2(x2+ 1)10 +C.
Câu 33. Họ tất cả các nguyên hàm của hàm số f(x) = xexlà
A.xex
2+C.B.xex+C.C.(x−1) ex+C.D.(x+ 1) ex+C.
Câu 34. Trong không gian Oxyz, mặt phẳng (P) : 2x−3z+ 2 = 0 có một vectơ pháp tuyến là
A.#»
n= (2; 3; 2).B.#»
n= (2; 0; −3).C.#»
n= (2; −3; 0).D.#»
n= (2; −3; 2).
Câu 35. Trong không gian Oxyz,mặt cầu (S) : x2+y2+z2−2x+ 2y−6z+ 2 = 0 cắt mặt phẳng(Oyz)theo
giao tuyến là một đường tròn có bán kính bằng:
A.1.B.2√2.C.√2.D.3.
Câu 36. Họ tất cả các nguyên hàm của hàm sốf(x) = x2+3
xlà
A.x3
3+ ln |x|+C.B.x3+ 3 ln |x|+C.C.x3+ ln |x|+C.D.x3
3+ 3 ln |x|+C.
Câu 37. Hàm số F(x)là một nguyên hàm của hàm số f(x)trên khoảng Knếu
A.F′′(x) = f(x).B.F(x) = f′′ (x).C.F′(x) = f(x).D.F(x) = f′(x).
Câu 38. Trong không gian Oxyz, cho hai điểm A(4; −2; 1) và B(0; −2; −1). Phương trình mặt cầu có đường
kính AB là
A.(x−2)2+ (y+ 2)2+z2= 20.B.(x+ 2)2+ (y−2)2+z2= 20.
C.(x−2)2+ (y+ 2)2+z2= 5.D.(x+ 2)2+ (y−2)2+z2= 5.
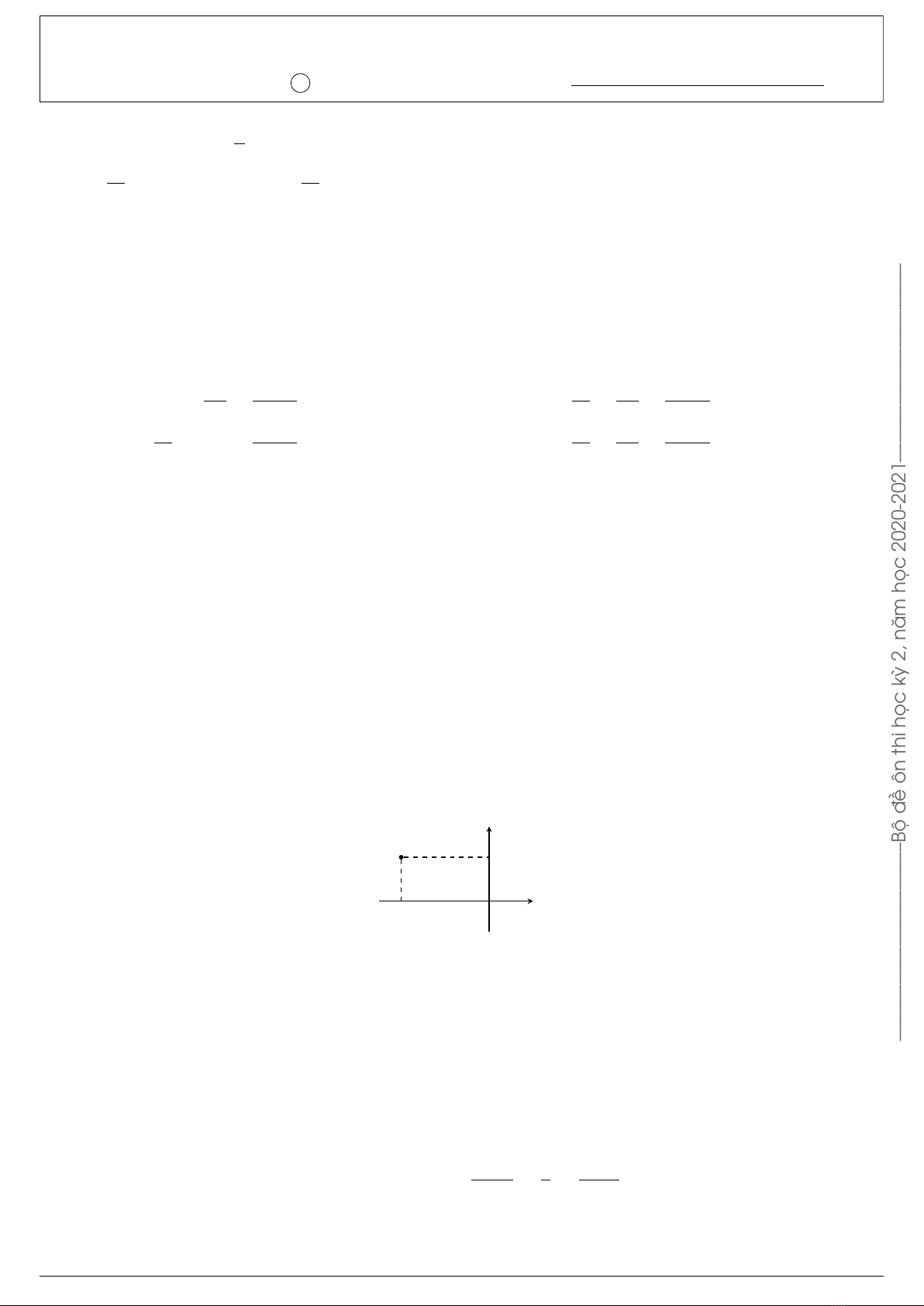
Câu 39. Trong mặt phẳng Oxy, số phức z=−2 + 4iđược biểu diễn bởi điểm nào trong các điểm ở hình vẽ
dưới đây?
A. Điểm C.B. Điểm A.C. Điểm D.D. Điểm B.
Câu 40. Trong không gian Oxyz, phương trình mặt cầu tâm I(−1; 0; 1), bán kính bằng 3là
A.(x−1)2+y2+ (z+ 1)2= 3.B.(x+ 1)2+y2+ (z−1)2= 9.
C.(x−1)2+y2+ (z+ 1)2= 9.D.(x+ 1)2+y2+ (z−1)2= 3.
Câu 41. Trong không gian Oxyz, điểm đối xứng với điểm A(1; −3; 1) qua đường thẳng d:x−2
−1=y−4
2=
z+ 1
3có tọa độ là
A.(−10; −6; 10).B.(4; 9; −6).C.(−4; −9; 6).D.(10; 6; −10).
Câu 42. Trong không gian Oxyz, cho mặt cầu (S) : (x−3)2+ (y−2)2+ (z−6)2= 56 và đường thẳng
∆ : x−1
2=y+ 1
3=z−5
1. Biết rằng đường thẳng ∆cắt (S)tại điểm A(x0;y0;z0)với x0>0. Giá trị của
y0+z0−2x0bằng
A.30.B.−1.C.9.D.2.
Bộ đề ôn thi học kỳ 2-Toán 12 Trang 3
——————————–Biên soạn:−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Câu 43.
Cho đồ thị hàm số y=f(x)(như hình vẽ). Diện tích Scủa hình phẳng (phần
tô đậm trong hình dưới) là
A.S=
−2
Z
0
f(x)dx+
3
Z
0
f(x)dx.B.S=
3
Z
−2
f(x)dx.
C.S=
0
Z
−2
f(x)dx+
0
Z
3
f(x)dx.D.S=
0
Z
−2
f(x)dx+
3
Z
0
f(x)dx.x
y
−2
3O
Câu 44. Cho hàm số f(x)liên tục trên Rvà
4
Z
0
f(x)dx= 2020. Giá trị của
2
Z
0
xf x2dxbằng
A.1010.B.2019.C.1008.D.4040.
Câu 45. Một vật chuyển động chậm dần đều với vận tốc v(t) = 150 −10t(m/s), trong đó tlà thời gian tính
bằng giây kể từ lúc vật bắt đầu chuyển động chậm dần đều. Trong 4giây trước khi dừng hẳn, vật di chuyển
một quãng đường bằng
A.150m.B.80m.C.100m.D.520m.
Câu 46. Trong không gian Oxyz, cho hai đường thẳng d:x
1=y
1=z
−2, d′:(x=−1−2t
y=t
z=−1−t
và mặt phẳng
(P) : x−y−z= 0. Biết rằng đường thẳng ∆song song với mặt phẳng (P), cắt các đường thẳng d, d′lần lượt
tại Mvà Nsao cho MN =√2(điểm Mkhông trùng với gốc tọa độ O). Phương trình của đường thẳng ∆
là
A.
x=−4
7+ 3t
y=4
7+ 8t
z=−8
7−5t
.B.
x=1
7+ 3t
y=−4
7+ 8t
z=−3
7−5t
.C.
x=1
7+ 3t
y=−4
7+ 8t
z=−8
7−5t
.D.
x=4
7+ 3t
y=−4
7+ 8t
z=−8
7−5t
.
Câu 47. Biết rằng F(x)là một nguyên hàm của hàm số f(x) = sin (1 −2x)và FÅ1
2ã= 1. Mệnh đề nào sau
đây đúng?
A.F(x) = −1
2cos (1 −2x) + 3
2.B.F(x) = cos (1 −2x).
C.F(x) = cos (1 −2x) + 1.D.F(x) = 1
2cos (1 −2x) + 1
2.
Câu 48. Cho hàm số y=f(x)liên tục, thỏa mãn f(x) = xÅ1 + 1
√x−f′(x)ã,∀x∈(0; +∞)và f(4) = 4
3.
Giá trị của
4
Z
1x2−1f′(x)dxbằng
A.457
30 .B.−263
30 .C.457
15 .D.−263
15 .
Câu 49. F(x)là một nguyên hàm của hàmf(x) = 3x2−ex+ 1 −mvới mlà tham số.Biết rằng F(0) = 2
vàF(2) = 1 −e2.Giá trị của mthuộc khoảng:
A.(5; 7).B.(6; 8).C.(4; 6).D.(3; 5).
Câu 50. Trong không gian Oxyz,cho hình hộp ABCD.A′B′C′D′có A(1; 0; 1);B(2; 1; 2) D(1; −1; 1)
A′(1; 1; −1).Giá trị cos Ä# »
AC′;
# »
B′D′ä
A.√3
3.B.√2
3.C.−√3
3.D.√2
3.
——————Hết——————
Bộ đề ôn thi học kỳ 2-Toán 12 Trang 4
——————————–Bộ đề ôn thi học kỳ 2, năm học 2020-2021——————————–
SỞ GIÁO DỤC VÀ ĐÀO TẠO:−−−−−−−−−−−−−−−
TRƯỜNG:−−−−−−−−−−−−−−−−
ĐỀ ÔN SỐ 2
ĐỀ KIỂM TRA HK 2, NĂM HỌC 2020-2021
MÔN TOÁN-THPT
Thời gian làm bài 90 phút, không tính thời gian giao đề
Câu 1. Hàm số F(x) = 1
xlà một nguyên hàm của hàm số nào dưới đây trên mỗi khoảng xác định?
A.−1
x2.B.1
x2.C.ln |x|.D.ln x.
Câu 2. Trong không gian Oxyz, phương trình mặt phẳng qua ba điểm A(−3; 0; 0),B(0; −2; 0) C(0; 0; 1)
được viết dưới dạng ax +by −6z+c= 0. Giá trị của T=a+b+clà
A.−1.B.−7.C.−11.D.11.
Câu 3. Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(0; 0; −6),B(8; 0; 0). Độ dài đoạn thẳng AB
bằng
A.10.B.14.C.100.D.2.
Câu 4. Tìm nguyên hàm F(x)của hàm số f(x) = x4−e3x+ cos 2x.
A.F(x) = 4x3−e3x
3+sin 2x
2+C.B.F(x) = x5
5−e3x
3+sin 2x
2+C.
C.F(x) = x5
5−3e3x+sin 2x
2+C.D.F(x) = x5
5−e3x
3−sin 2x
2+C.
Câu 5. Cho f, g là hai hàm liên tục trên [1; 3] thỏa mãn điều kiện
3
Z
1
[f(x) + 3g(x)] dx= 10 đồng thời
3
Z
1
[2f(x)−g(x)] dx= 6. Tính
3
Z
1
[f(x) + g(x)] dx.
A.8.B.9.C.6.D.7.
Câu 6. Cho hai số phức z1= 5 −3i,z2=−1 + 2i. Tổng phần thực, phần ảo của tổng hai số phức đã cho
là: A.S= 4.B.S= 3.C.S= 5.D.S= 7.
Câu 7. Biết rằng
ln a
Z
0
exdx= 1, khi đó giá trị của alà:
A.a= 4.B.a= 1.C.a= 3.D.a= 2.
Câu 8. Trong mặt phẳng Oxy, điểm Mtrong hình vẽ bên là điểm biểu diễn số phức z. Số phức ¯zlà
x
y
O
M
−2
1
A.1−2i.B.−2−i.C.1 + 2i.D.−2 + i.
Câu 9. Mệnh đề nào sau đây sai?
A.Zkf(x)dx=kZf(x)dxvới mọi hằng số kvà với mọi hàm số f(x)liên tục trên R.
B.Zf′(x)dx=f(x) + Cvới mọi hàm số f(x)có đạo hàm trên R.
C.Z[f(x) + g(x)] dx=Zf(x)dx+Zg(x)dx, với mọi hàm số f(x), g(x)liên tục trên R.
D.Z[f(x)−g(x)] dx=Zf(x)dx−Zg(x)dx, với mọi hàm số f(x), g(x)liên tục trên R.
Câu 10. Trong không gian Oxyz, cho đường thẳng ∆:x−2
−3=y
1=z+ 1
2. Tọa độ điểm Mlà giao điểm của
∆với mặt phẳng (P):x+ 2y−3z+ 2 = 0:
A.M(1; 0; 1).B.M(2; 0; −1).C.M(−1; 1; 1).D.M(5; −1; −3).
Bộ đề ôn thi học kỳ 2-Toán 12 Trang 5












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



