5 đ ki m tra h c kỳ II Toán 9 (2009-2010) _ Có đáp ánề ể ọ
Đ ề
1
MA TR N Đ KI M TRA H C KỲ IIẬ Ề Ể Ọ
MÔN TOÁN KH I 9Ố
NĂM H C: 2009 – 2010Ọ
Các ch đủ ề Nh n bi tậ ế Thông hi uểV n d ngậ ụ T ngổ
c ngộ
TN TL TN TL TN TL
H ph ng trình b cệ ươ ậ
nh t hai n ấ ẩ S câuố111115
S đi mố ể 0,25 1,0 0,25 2,0 0,25 3,75
Hàm s ố
2( 0)y ax a= ≠
S câuố22
S đi mố ể 0,5 0,5
Ph ng trình b c haiươ ậ
m t nộ ẩ S câuố1 1 1 3
S đi mố ể 0,25 0,25 1,5 2,0
Góc v i đ ng trònớ ườ S câuố21 1 4
S đi mố ể 0,5 2,0 0,5 3,0
Hình tr – hình nón –ụ
hình c uầS câuố2 1 3
S đi mố ể 0,5 0,25 0,75
T ng c ngổ ộ S câuố417311 17
S đi mố ể 1,0 1,0 1,75 5,5 0,25 0,5 10,0
Đ KI M TRA H C KỲ IIỀ Ể Ọ
MÔN TOÁN KH I 9Ố
NĂM H C : 2009 – 2010Ọ
I) Tr c nghi mắ ệ : ( 3 đi m)ể
Hãy khoanh tròn ch đ ng tr c câu mà em ch n.ữ ứ ướ ọ
1) Ph ng trình nào sau đây là ph ng trình b c nh t hai n ?ươ ươ ậ ấ ẩ
A.
2005x xy+ =
; B.
0 0 9x y+ =
; C.
1 1 8
x y
+ = −
; D.
3 12x y+ =
2) Ph ng trình đ ng th ng đi qua hai đi m ươ ườ ẳ ể
(2; 2)C−
và
( 1;3)D−
là :
A.
5 4
3 3
y x
−
= +
; B.
5 4
3 3
y x= +
; C.
5 4
3 3
y x= −
; D.
5 4
3 3
y x
−
= −
3) C p s nào sau đây là nghi m c a h ph ng trình ặ ố ệ ủ ệ ươ
1
2
x y
x y
− =
+ = −
?
A.
;B.
1 3
;
2 2
= − = −
x y
; C.
3 1
;
2 2
= =
x y
; D.
1 3
;
2 2
x y
= = −
4) Cho hàm s ố
2
( ) 2y f x x= = −
. K t lu n nào sau đây ế ậ sai ?
A.
( ) ( )f x f x= −
v i m i x.ớ ọ
B.
>( ) 0f x
v i m i x.ớ ọ
C.
( )f x
đ ng bi n khi ồ ế
0x
<
; ngh ch bi n khi ị ế
0x
>
D. N u ế
( ) 32f x = −
thì
4x
= ±
2009-2010/dtvt 1
1
5 đ ki m tra h c kỳ II Toán 9 (2009-2010) _ Có đáp ánề ể ọ
5) Đi m nào sau đây thu c đ th hàm s ể ộ ồ ị ố
2
1
2
y x=
A.
( )
2; 2− −
;B.
( )
2;2
; C.
1
1; 2
− −
; D.
( )
4;4
6) Các h s a và c c a ph ng trình b c hai ( n x ) ệ ố ủ ươ ậ ẩ
+ =
2
2 3x x m
là:
A. 2 và 3; B. 2 và
m−
; C. 3 và
m−
; D. 2 và m
7) Bi t th c ệ ứ
/
∆
c a ph ng trình ủ ươ
2
4 6 1 0x x− − =
là:
A. 5 ; B. 13 ; C. 25 ; D. 52
8) Di n tích c a hình qu t tròn có góc tâm 90ệ ủ ạ ở 0, bán kính 2 cm là :
A.
π
(cm) ; B.
π
(cm2) ; C.
2
2 ( )cm
π
; D.
2
( )
2cm
π
9) Cho
∆
ABC n i ti p đ ng tròn (O), bi t ộ ế ườ ế
µ
µ
0 0
60 ; 45B C= =
. Khi đó
»
sñBC
là :
A.
0
75
; B.
0
105
; C.
0
135
; D.
0
150
10) Hình tri n khai m t xung quanh c a m t hình nón là m t hình qu t. N u bán kính qu t là 16ể ặ ủ ộ ộ ạ ế ạ
cm, s đo cung là 120ố0 thì đ dài đ ng sinh c a hình nón là : ộ ườ ủ
A.
16 cm
; B.
8cm
; C.
16
3cm
; D.
4cm
11) Th tích c a hình tr có bán kính đáy 1 cm, chi u cao g p đôi bán kính đáy là :ể ủ ụ ề ấ
A.
3
4 ( )cm
π
; B.
3
2 ( )cm
π
; C.
3
( )cm
π
; D.
3
0,5 ( )cm
π
12) Th tích hình c u có bán kính 6 cm là :ể ầ
A.
3
723,46 ( )cm
; B.
3
904,78( )cm
; C.
3
1808,64 ( )cm
; D.
3
904,32 ( )cm
II) T LU N: ( 7 đi m)Ự Ậ ể
Câu 1: (1 đi m) Gi i h ph ng trình ể ả ệ ươ
2 3 11
4 6 5
x y
x y
− =
− + =
Câu 2: (2 đi m) Cho hai hàm s ể ố
2
y x=
và
2 3y x= − +
.
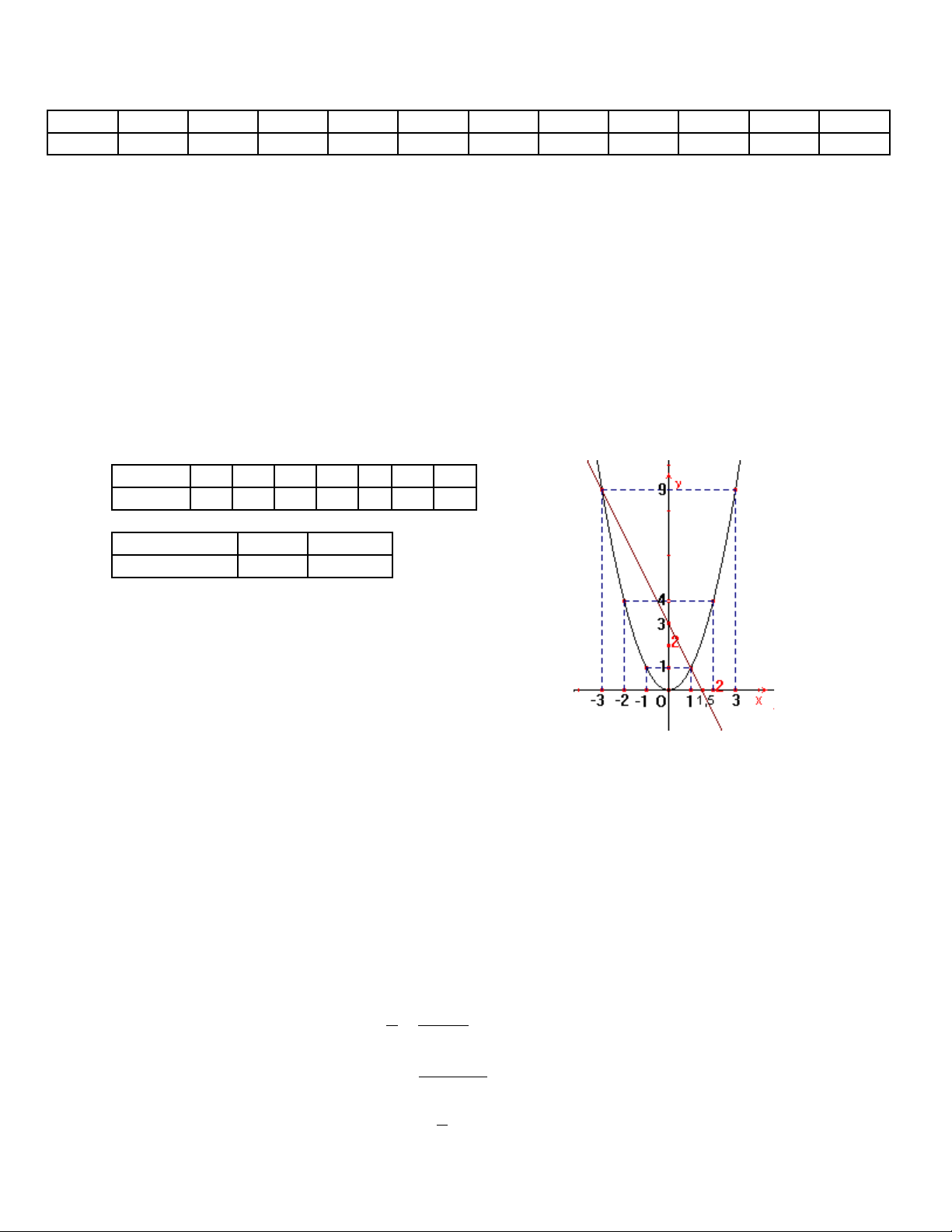
a) V các đ th c a hai hàm s này trên cùng m t h tr c t a đ .ẽ ồ ị ủ ố ộ ệ ụ ọ ộ
b) Tìm t a đ giao đi m c a hai đ th đó b ng hình v .ọ ộ ể ủ ồ ị ằ ẽ
Câu 3: (1,5 đi m) Cho ph ng trình ể ươ
2 2
2 (2 1) 2 0x m x m+ − + − =
( m là tham s )ố
a) Tìm giá tr m đ ph ng trình có nghi m ị ể ươ ệ
12x=
.
b) Dùng h th c Vi-ét đ tìm nghi m ệ ứ ể ệ
2
x
.
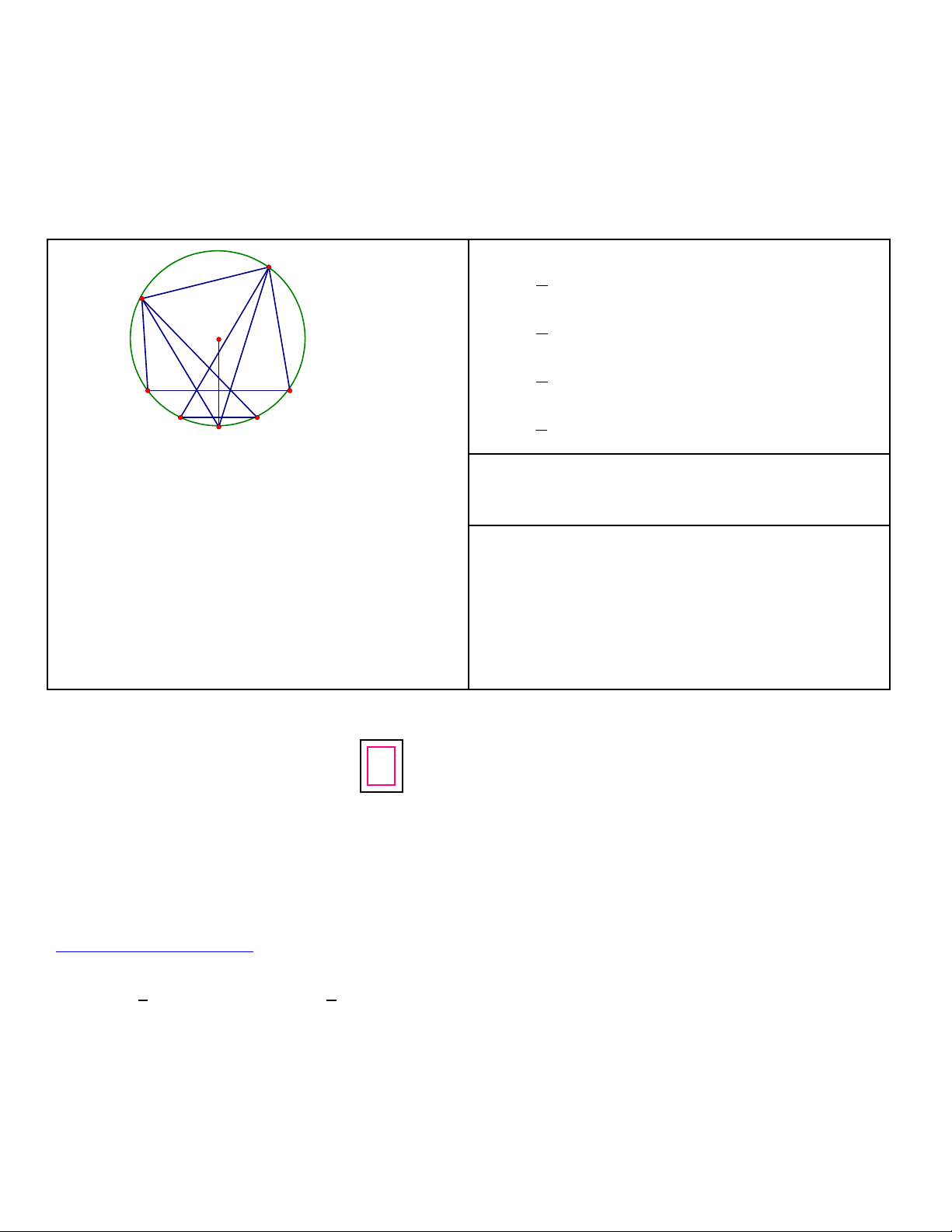
Câu 4: (2,5 đi m) Cho t giác ABCD n i ti p đ ng tròn (O). S là đi m chính gi a c a cung AB, SC vàể ứ ộ ế ườ ể ữ ủ
SD c t AB t i E và F.ắ ạ
a) Ch ng minh t giác CDFE n i ti p.ứ ứ ộ ế
b) DE và CF kéo dài c t (O) l n l t t i M và N. Ch ng minh OS ắ ầ ượ ạ ứ
⊥
MN.
ĐÁP ÁN
I) TR C NGHI MẮ Ệ : ( 3 đi m)ể
M i câu đúng đ c 0,25 đi mỗ ượ ể
2009-2010/dtvt 2
2
5 đ ki m tra h c kỳ II Toán 9 (2009-2010) _ Có đáp ánề ể ọ
1 2 3 4 5 6 7 8 9 10 11 12
D A B B B B BB D A B B
II) T LU N: ( 7 đi m)Ự Ậ ể
Câu 1: (1 đi m) Gi i h ph ng trình ể ả ệ ươ
2 3 11
4 6 5
x y
x y
− =
− + =
4 6 22
4 6 5
x y
x y
− =
⇔− + =
0 0 27
4 6 5
x y
x y
+ =
⇔− + =
(0,5 đi m)ể
Vì ph ng trình ươ
0 0 27x y+ =
vô nghi mệ(0,25 đi m)ể
Nên h ph ng trình vô nghi m ệ ươ ệ (0,25 đi m)ể
Câu 2: (2 đi m)ể
a) * B ng giá tr : M i b ng đúng đ c 0,25 đi mả ị ỗ ả ượ ể
x -3 -2 -1 0 1 2 3
y = x29 4 1 0 1 4 9
x 0 1,5
y = –2x + 3 3 0
* Đ th v đúng đ c 1 đi mồ ị ẽ ượ ể
b) 0,5 đi m ể
D a vào hình v ta có t a đ giao đi m c a hai đ th là ự ẽ ọ ộ ể ủ ồ ị
(–3; 9) vaø (1; 1)
Câu 3: (1,5 đi m)ể
Cho ph ng trình ươ
2 2
2 (2 1) 2 0x m x m+ − + − =
( m là tham s ) ố(1)
a) Thay
12x=
vào ph ng trình (1) ta đ c:ươ ượ
2 2
2.2 (2 1).2 2 0m m+ − + − =
(0,25 đi m)ể
2
8 4 2 2 0m m⇔ + − + − =
2
4 4 0m m⇔ + + =
2
(2 ) 0m⇔ + =
(0,25 đi m)ể
2 0m⇔ + =
2m
⇔ = −
(0,25 đi m)ể
b) Theo h th c Vi-et, ta có ệ ứ
2
1 2
2
.2
c m
x x a
−
= =
(*) ( 0,25 đi m)ể
Thay
12; 2x m= = −
vào (*) ta đ c ượ
2
2
( 2) 2
2 1
2
x− −
= =
( 0,25 đi m)ể
2
1
2
x⇔ =
( 0,25 đi m)ể
2009-2010/dtvt 3
3
5 đ ki m tra h c kỳ II Toán 9 (2009-2010) _ Có đáp ánề ể ọ
Câu 4 : ( 2,5 đi m)ể
c
1
F
E
O
A
B
D
C
S
M
N
(0,5 đi m)ể
a) Xét t giác CDứFE, có:
·
¼
»
( )
1
2
D FB sñD CB sñAS= +
¼
»
( )
1
2sñD CB sñBS= +
¼
1
2sñD CS=
(0,75 đi m)ể
·
¼
1
2
D CS sñD AS=
(0,25 đi m)ể
V y ậ
·
·
0
180D FB D CS+ =
(0,25 đi m)ể
Do đó t giác CDFE n i ti p ( vì có t ng hai góc đ iứ ộ ế ổ ố
b ng 108ằ0) (0,25 đi m)ể
b) Vì t giác CDFE n i ti pứ ộ ế
Nên
·
·
SD N SCM=
(cùng ch n ắ
»
EF
) (0,25
đi m)ể
»
»
NS M S⇒ =
c a đ ng tròn (O)ủ ườ
Do đó OS
⊥
MN. (0,25 đi m)ể
Đ ề
2
PHÒNG GIÁO D C VÀ ĐÀO T O Ụ Ạ Đ KI M TRA H C KỲ IIỀ Ể Ọ
TR NG THCSƯỜ Năm h c 2009 – 2010ọ
-oOo- Môn TOÁN - L p 9ớ
Th i gian làm bài: 90 phútờ
(Không k th i gian phát đ )ể ờ ề
***************************
PH N TR C NGHI MẦ Ắ Ệ : (3,0 đi m)ể
1. Đ th hàm s y = axồ ị ố 2 đi qua đi m A( – 3; 3), khi đó :ể
A. a =
1
3
B. a = –
1
3
C. a = 3 D. a = – 3
2. Parabol (P) : y = – 2x2 và đ ng th ng (∆): y = m có đi m chung khi và ch khi:ườ ẳ ể ỉ
A. m > 0 B. m ≥ 0 C. m < 0 D. m ≤ 0
3. S đi m chung c a đ ng th ng (∆): y = – x + 2008 và Parabol (P): y = xố ể ủ ườ ẳ 2 là:
A. Không B. M t C. Hai D. Nhi u h n hai.ộ ề ơ
4. Hai s 6 và – 4 là hai nghi m c a ph ng trình:ố ệ ủ ươ
A. x2 + 2x – 24 = 0 B. x2 + 2x + 24 = 0 C. x2 – 2x – 24 = 0 D. x2 – 2x + 24 = 0
2009-2010/dtvt 4
4
5 đ ki m tra h c kỳ II Toán 9 (2009-2010) _ Có đáp ánề ể ọ
5. Ph ng trình xươ 2 + 3x – 100 = 0 có hai nghi m phân bi t xệ ệ 1, x2; Khi đó giá tr c a ị ủ
S = x1 + x2 và P = x1. x2 là:
A. S = 3; P = 100 B. S = 3; P = –100 C. S = – 3; P = 100 D. S = – 3; P = –100
6. Ph ng trình xươ 2 – 2x – 4m – 3 = 0 có hai nghi m phân bi t khi và ch khi:ệ ệ ỉ
A. m > – 1 B. m > – 2 C. m > 1 D. m > 2
7. Cho đ ng tròn tâm O, bán kính R và dây cung AB = R. Trên cung nhò AB l y đi m M.ườ ấ ể
S đo c a ố ủ
·
AMB
là:
A. 600 B. 900 C. 1200 D. 1500
8. T giác nào d i dây không th n i ti p trong m t đ ng tròn ?ứ ướ ể ộ ế ộ ườ
A. Hình thang cân. B. Hình thoi C. Hình ch nh t D. Hình vuông.ữ ậ
9. A, B là hai đi m trên đ ng tròn tâm O bán kính R. Bi t AB = Rể ườ ế
3
, khi đó s đo c a ố ủ
·
AOB
là:
A. 1200 B. 900 C. 600 D. 450
10. N u bán kính m t c u tăng g p đôi thì di n tích xung quanh c a m t c u tăng:ế ặ ầ ấ ệ ủ ặ ầ
A. g p hai l n. B. g p b n l n. C. g p sáu l n. D. g p tám l n. ấ ầ ấ ố ầ ấ ầ ấ ầ
PH N T LU NẦ Ự Ậ : ( 7 đi m)ể
Bài 1: (4,0 đi m)ể
1) V đ ng th ng (∆): y = x + 4 và parabol (P): y = ẽ ườ ẳ
1
2
x2 trên cùng m t h tr c t a đ . D a vào hìnhộ ệ ụ ọ ộ ự
v hãy xác đ nh t a đ giao đi m c a (∆) và (P).ẽ ị ọ ộ ể ủ
2) Gi s xả ử 1, x2 là hai nghi m c a ph ng trình: xệ ủ ươ 2 – 20
2
x – 60 = 0; không gi i ph ng trình,ả ươ
hãy tính giá tr bi u th c: A = ị ể ứ
2 2
1 2
x x+
.
Bài 2: (3,0 đi m) ể
Cho đ ng tròn đ ng kính AB và đi m D n m trên cung AB ( D khác A và B). D ng ườ ườ ể ằ ự
hình bình hành ABCD, h DM vuông góc v i AC (M ạ ớ
∈
AC). Ch ng minh:ứ
1)
·
DBC
= 900 , suy ra t giác BCDM n i ti p trong m t đ ng tròn.ứ ộ ế ộ ườ
2)
·
BMC
=
·
ABD
.
-----H T-----Ế
ĐÁP ÁN
♣ PH N TR C NGHI MẦ Ắ Ệ : ( 3,0 đi m)ể
Câu 1 2 3 4 5 6 7 8 9 10
Đáp án A D C C D A D B A B
Bi u đi mể ể 0,25 0,50 0,25 0,25 0,25 0,25 0,25 0,25 0,50 0,25
♣ PH N T LU NẦ Ự Ậ : ( 7,0 đi m) ĐI Mể Ể
Bài 1: ( 4,0 đi m)ể
Câu 1: ( 2,0 đi m) ể
- Hình v :ẽ
2009-2010/dtvt 5
5